车辆转弯时内轮差的运动学理论模型1)

李逸良 邱信明

(清华大学航天航空学院，北京100084)

大学生园地

车辆转弯时内轮差的运动学理论模型1)

李逸良 邱信明2)

(清华大学航天航空学院，北京100084)

基于刚体运动学知识，利用速度投影定理建立了针对单车、半挂车的最大内轮差的运动学理论分析模型.模型可以给出车辆转弯时不同车轮的轨迹，并得出内轮差的准确计算公式.通过定量讨论车辆最大内轮差随车身尺寸、回转半径的变化规律，对于行人和驾驶员提出了具体的操作建议，以避免内轮差造成的交通事故.

内轮差,半挂车,轴距,速度投影定理,交通安全

由于车辆自身的体积，转弯时其前后轮的运行轨迹并不相同.内后轮的轨迹半径要小于内前轮的轨迹半径，这意味着车辆转弯过程中会向着圆心的方向不断靠近.转弯时车辆内前轮的转弯半径与内后轮的转弯半径之差，通常被称为内轮差.如图 1所示，由于内轮差的存在，前后内车轮轨迹之间会形成一个危险区域，进入这个区域的行人和非机动车很容易被车身后半部卷入.此外，由于我国汽车驾驶员位置在车辆左侧，车身右前侧、右侧后视镜下方是驾驶员的视线盲区；大卡车的驾驶室相对于路面的行人又很高，驾驶员不容易注意到危险区域内的行人和非机动车.如果内轮差现象被汽车司机、行人和非机动车忽视，右转弯时就会带来严重的交通事故[1].

图1 内轮差引起的路面危险区域示意图[2]

以往人们针对这个现象的研究，并没有给出内轮差的准确定义.通常是从假设车辆前后轮轨迹均为圆形的角度出发，半定性地分析内轮差的现象，如褚正清等[3]、李铁洪等[4]、陈思嘉[5]的研究.为了定量分析车辆转弯过程中向圆心靠近的程度，本文试图给出一种内轮差的准确数学定义，并利用理论力学中运动学的知识，定量分析影响内轮差的各种因素.

1 刚体运动学知识介绍

在建立内轮差的理论模型之前，先简要回顾一下《理论力学》中刚体运动学的相关概念和定理.关于物体最简单的力学模型是质点，即一个只有质量、无体积和形状的无限小的点.如果物体的运动和变形尺度远远大于自身尺度，则可以简化为质点进行分析，如分析飞机轨迹时的飞机，或者卫星轨道时的卫星.但如果关注的运动尺寸与物体自身尺度相当，则需要把物体当成刚体来处理，如分析自身姿态时的飞机或者卫星.作为最基本的力学模型之一，刚体是由无穷多质点构成的有限大小的物体，有质量也有体积和形状.刚体在任何情况下都不发生变形，因此任何质点之间的距离始终保持不变[6].

如图2所示，假设一个刚体上的两个任意点A和B，由刚体的定义可知，A点和B点之间的连线距离始终不变.根据理论力学的刚体上两点的速度关系

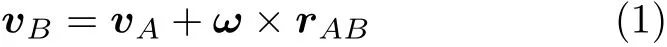
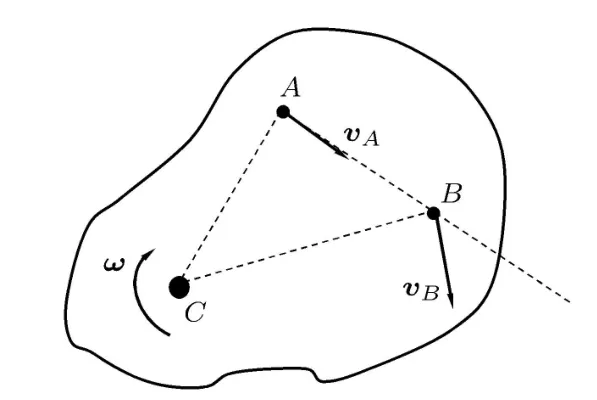
图2 刚体上点的速度分析

这里ω是刚体的转动角速度向量，方向垂直于纸面，rAB是两点之间的向径.由式(1)在向量rAB上的投影显然有

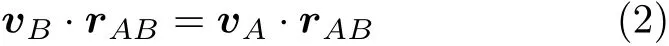
上式是刚体的速度投影定理，即刚体上任意两点的速度在这两点的连线上的投影相等.速度投影定理也可由刚体的概念直接得出，若两点的速度在连线上的投影不相等，两点间的距离就会改变，与刚体上任意两个质点之间距离始终不变的基本假设相矛盾[6].

过A和B两点，分别做它们速度的垂线，两条垂线的交点C在这一瞬时速度为零，称为刚体的速度瞬心，简称瞬心.瞬心可能在刚体上，也可能在刚体外(称为刚体的延拓部分).这一瞬时，刚体上任何点的速度分布，就如同刚体在绕瞬心C做定轴转动一样.

2 汽车内轮差的理论分析模型

接下来，我们将利用上述知识建立内轮差问题的运动学理论分析模型.如图3所示，取汽车底盘的工字型钢架为刚体研究对象，设车的前后轮间距为l，A点代表内前轮，B点代表内后轮.忽略离心力所引起的车辆侧滑与轮胎变形所引起的侧向偏离对运动轨迹的影响.设车辆右转弯时，A点速度恒定为vA，A点轨迹为π/2圆弧(半径为R、圆心为O)然后接直线段.

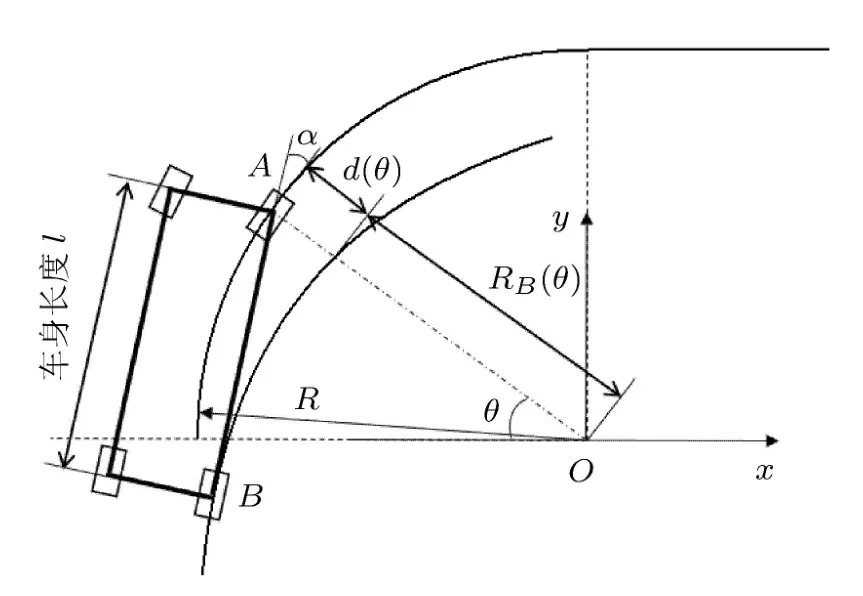
图3 单车内轮差的理论模型示意图

如图3所示，以O为坐标原点建立平面直角坐标系Oxy，并定义θ角处的内轮差d(θ)，是A点轨迹和B点轨迹沿θ方向的径矢之差，即

需要指出的是，上式中对应于相同的位置θ,A点和B点的径矢处于不同的时刻.其中A点的时刻t=Rθ/vA，而显然B点的时刻要迟于A点.

定义车辆转弯过程中的最大内轮差为

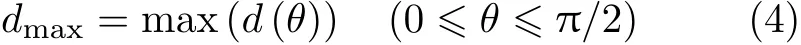
在t时刻,A点位置为 (xA,yA)=(-Rcosθ,Rsinθ)，其速度沿着该点轨迹的切线方向w1= (sinθ,cosθ)，其中θ=vAt/R.由于汽车后轮不转向，因此任何时刻右后轮B点的速度方向始终沿着AB连线方向，即w2=(xA-xB,yA-yB)/l.则A点速度方向与和AB连线间的夹角α满足

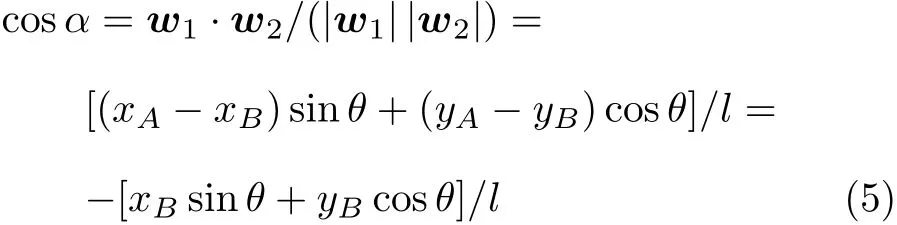
因此，由速度投影定理可知B点速度的分量形式

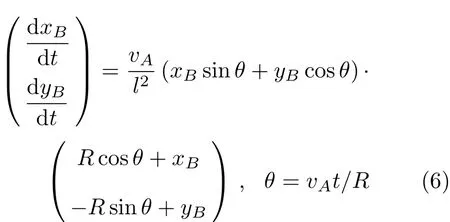
利用初始条件：t=0时刻，B点坐标(-R,-l)，对上式进行积分即可得B点的轨迹，同时可以计算出内轮差.

对于轴距l=2m的汽车，计算出不同内前轮轨迹半径R下，最大内轮差的数据列在表1中.由表中的数据可知，随着转弯半径R的增大，最大内轮差dmax单调降低.可见，为减小内轮差，应尽量转大弯，而不应转小弯.

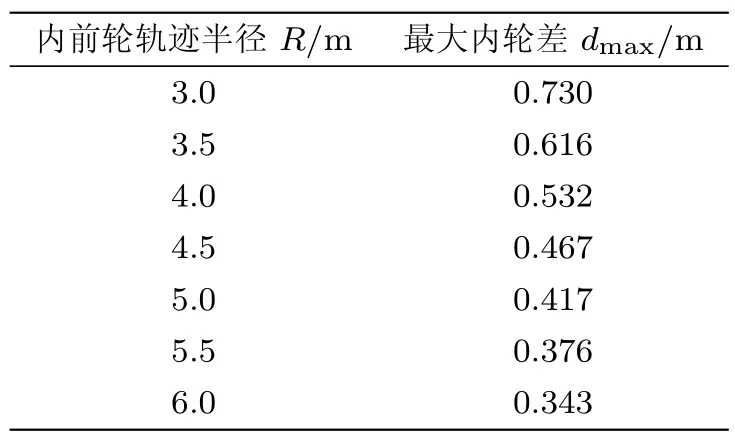
表1 不同转弯半径下的最大内轮差(轴距l=2m)

如图4所示，若内前轮轨迹半径为确定值R= 4m，在图中用最靠上的黑实线表示；带图标的线为对应不同轴距l=1.5m,2.0m,2.5m,3.0m汽车的内后轮轨迹；其中箭头指向是l=1.5m的汽车在不同时刻的车身位置.显然，除转弯半径R外，车身轴距l也是影响内轮差大小的一个重要因素，当R半径相同时，轴距较长的车内轮差明显更大.

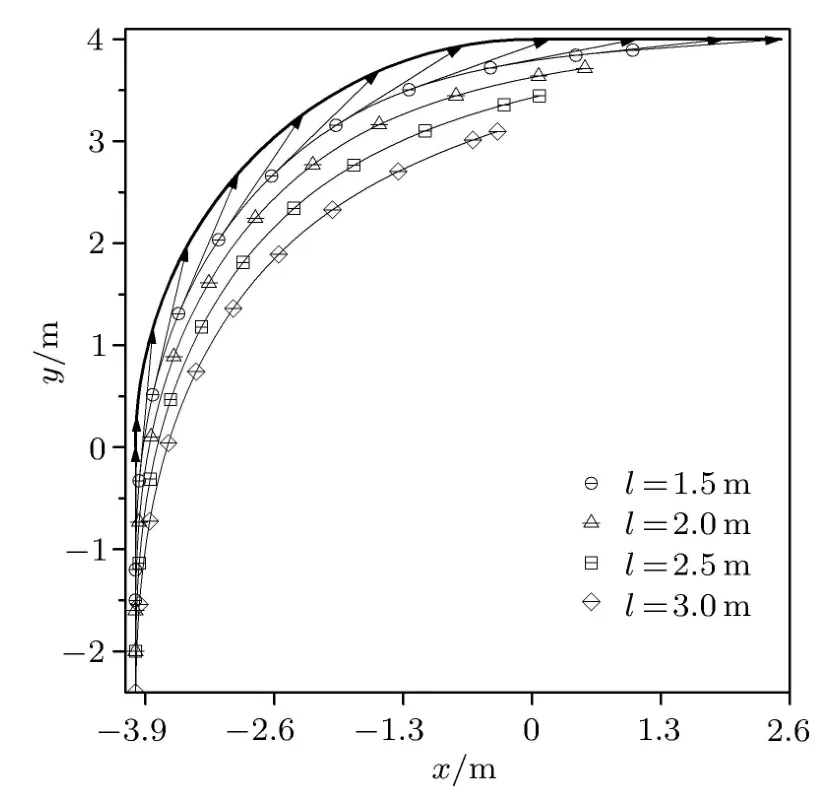
图4 不同轴距l的车辆转弯时A点和B点的轨迹(R=4m)

对于汽车而言，方向盘打到极限位置，外侧前轮距离转向中心 (瞬心)的距离通常定义为最小转弯半径r.如图5所示，在已知车宽w和轴距l的情况下，容‡易换算出最小的·内前轮轨迹半径Rmin，即+l2.通过查阅不同车型的数据资料，将车身尺寸、最小转弯半径、内前轮最小转弯半径列于表2中.

图5 转弯半径与内前轮轨迹半径

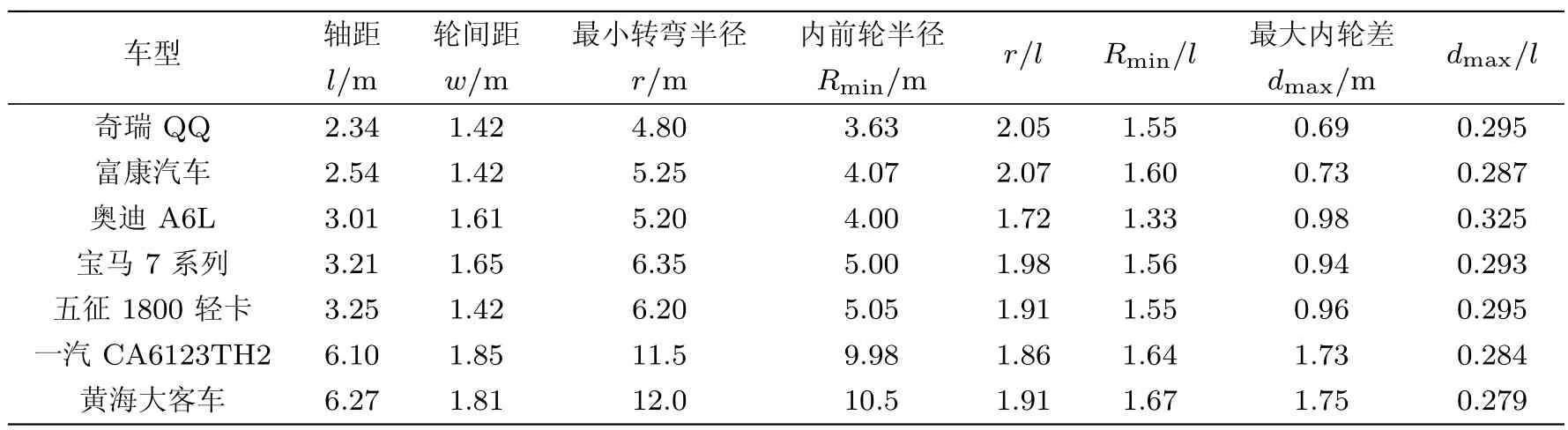
表2 典型车型的尺寸[7]和最大内轮差

图6给出了无量纲化内轮差和转弯半径的关系图，可见内轮差随转弯半径的增大而降低.对于表2给出的典型车型，用不同的图标在曲线上标示了其dmax和Rmin所在的位置，此处对应该车方向盘打到极限位置时的最大内轮差，实际产生的内轮差在该点右侧的曲线上.

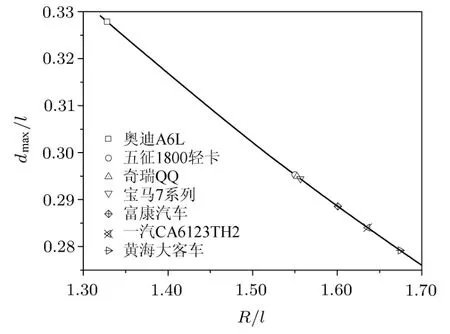
图6 汽车内轮差随内前轮(A点)转弯半径的变化关系图

根据表2给出的数据，典型车型的最小转弯半径与轴距之比都约为2左右，即r/l≈2.但由于轴距l不同，奇瑞QQ等小型车的内轮差仅为dmax= 0.69m，而黄海等大型车则达到dmax=1.73m.由表2可知，所列的典型车型均有dmax/l＜1/3，即最大内轮差小于1/3轴距.那么行人和非机动车要保证自身安全，需要与汽车保持车长1/3以上的距离.

3 半挂车内轮差的理论分析模型

大货车、水泥搅拌车等半挂车，可认为是两个刚体(牵引头、主车身)连接而成的组合体，如图7所示.设图中牵引头AB轴距l1，车身BC轴距l2，刚体AB和BC在B点通过无摩擦转轴(通常为大王销)相互连接.考察牵引头中线AB和车身中线BC的运动规律.假设A点轨迹为圆弧，半径为R，圆心为O.以O为坐标原点，建立平面直角坐标系Oxy,如图7所示，并以顺时针方向为转角θ的正方向.图中A,B,C三点的轨迹用虚线描绘，而内前轮A′和内后轮C′的轨迹用黑实线描绘.

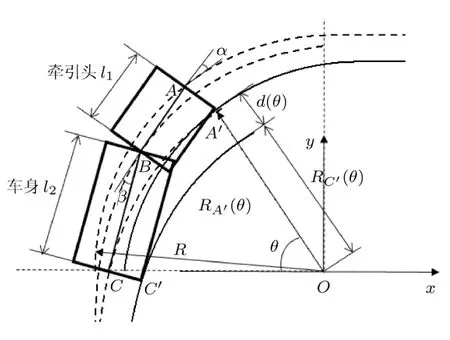
图7 半挂车内轮差的理论模型示意图

由上节汽车的分析模型，点A和点B的运动规律与单车的运动规律完全相同，B点的关于时间的运动方程也与上节完全相同.而点C的速度方向始终与BC平行，速度大小可由速度投影定理得到.对于时间积分可得C点在任意时刻的位置.计算A,C点轨迹之差d′max

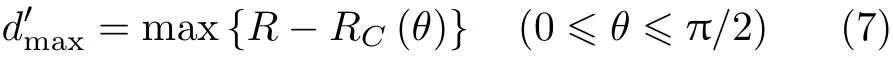
需要指出d′max并非最大内轮差，半挂车的最大内轮差应为A′和C′的轨迹之差，即

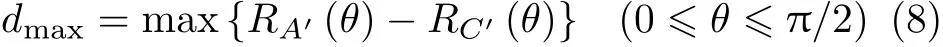
如果A点转弯半径为R=6m，对于不同轴距l1,l2的半挂车可以得到其转弯时的轨迹如图8所示.图中最上方的黑实线为A点轨迹，带图标的三条曲线为C点轨迹.其中带弯折的箭头表示不同时刻车身AB-BC线的方位，对应车身尺寸为l1=1.5m,l2=3.0m.显然，当A轨迹半径R相同时，轴距较长的车d′max明显较大.

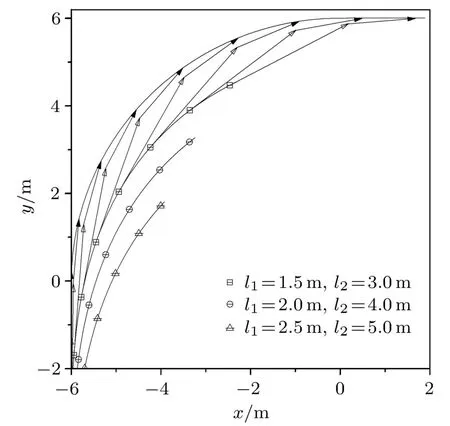
图8 不同轴距的半挂车转弯时C点的轨迹(R=6m)

表3给出了A点和C点轨迹之差最大值d′max与车身/牵引头轴距比l2/l1的变化关系.可见d′max随l2/l1的增加而增加.接下来我们考虑车身宽度对内轮差的影响.当车身宽度b1,b2改变而其他条件不变时，作为车身中线的A,B,C三点轨迹均不发生变化.A′点与A点轨迹相比较，相当于沿着径向向内移动的距离，其中α为BA与A点轨迹切线方向的夹角.同理，C′点与C点轨迹相比较，相当于沿着径向向内移动的距离.其中β为线段BC方向与C点轨迹切向的夹角.那么内轮差公式可写为

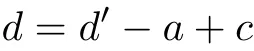
由公式知，牵引头宽度b1增大时，内轮差d线性减小；车身宽度b2增大时，内轮差d线性增大.对于车宽b1=b2=1.8m，R/l1=5的半挂车，计算得到的最大内轮差dmax见表3.通过查阅资料，一些典型半挂车的数据列于表4中.将表3和表4中数据整理得到图9.从图9中可以看出，当R/l1=5时，典型半挂车的dmax/l1均在 1以内.因为没有查到半挂车的最小转弯半径数据，因此得不到Rmin和最大的内轮差.如果有读者能够找到半挂车的最小转弯半径，可自行计算最大内轮差.从当前数据来看，建议行人和非机动车为了保证自身安全，至少要与半挂车转弯轨迹保持约牵引车长度l1的距离.

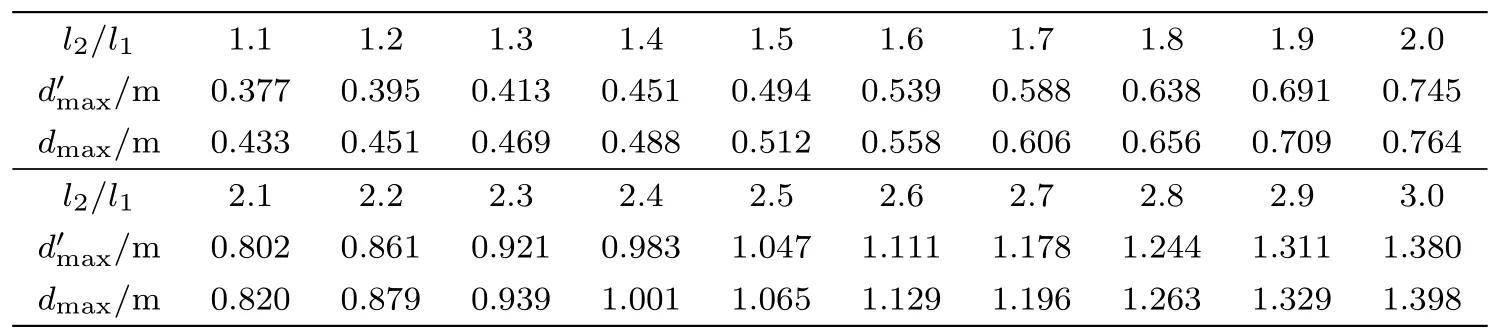
表3 半挂车内轮差与轴距比(l1=1.5m，R=7.5m，b1=b2=1.8m)

表4 典型半挂车的尺寸[7]与最大内轮差(R/l1=5)

图9 半挂车的内轮差随轴距比变化规律(R/l1=5)

4 讨论

本文基于理论力学的运动学知识，建立了汽车和半挂车转弯时内轮差问题的理论模型.此模型可以给出车辆转弯时不同车轮的轨迹，并得出内轮差的准确计算公式.通过定量分析得到车辆最大内轮差随车身尺寸、回转半径的变化规律：内轮差随车身长度增加而增大，随回转半径的减小而增大.

对于驾驶者而言，为了减小内轮差，应采用尽可能大的转弯半径R[8].此外，汽车右转时，驾驶员是通过车辆右侧后视镜观察路况的，为了减小视觉盲区和观察误差应尽量降低速度[9].当前的大型客车和半挂车的倒后镜，有些已经考虑了缩小视觉盲区的因素，比如有些车辆倒后镜由多块不同角度的镜子组成，斜向下方的倒后镜，可以起到缩小视觉盲区的作用.而少数高端的轿车，已经配备围绕车身的倒车雷达，若周围物体、行人或车辆与本车距离过近，会自动报警.这些主动控制方案，可以帮助驾驶员避免内轮差产生的交通事故.

内轮差的危害对象通常是汽车右侧的行人和非机动车.为了避免内轮差带来的危险，行人和非机动车需要保持和转弯汽车的安全距离，不要超越正在右转弯的车辆.对于一体的单个汽车而言，至少与汽车保持车身长度1/3以上的距离；对于半挂车而言，保持距离需要在牵引头长度以上.

从车辆设计者的角度，单纯为减少内轮差而改变车身尺寸是不现实的.本文的理论模型基于后轮不转向的基本假设，因此后轮的速度沿着车身方向，这对于当前的绝大多数车型都是适用的.但是随着技术的发展，高端的概念车已经可以实现四轮转向(也叫全轮转向)，如在保时捷电动跑车的宣传中，号称时速50km以下时后轮偏转方向与前轮相反，以减少转弯半径；而时速超过50km时，后轮偏转方向将与前轮相同，以获得更好的循迹性和高速过弯性能[10].这种情况下，内轮差的概念其实已经不适用了.极限状态下车可以实现垂直车身长度方向的运动，就像四轮行李箱一样，这时必须配合复杂的车身控制系统才能保持需要的姿态.虽然目前这些技术距离家用车、大型车的应用还有距离，但将来的应用是完全可以预期的，只是时间的问题.

1 陈诗佳.半挂车路口转弯时刮倒一对母子 “内轮差”是主因.新蓝网·浙江网络广播电视台,2016.http：//n.cztv.com/ news/12014073.html

2 朱文. 了解 “内轮差”，远离转弯的大货车、工程车.海宁日报,2012.http：//hnrb.zjol.com.cn/hnrb/html/2012-12/13/ content 207927.htm.

3 褚正清,刘家保,宋星.货车右转弯内轮差的建模研究.河北北方学院学报,2015,31(5)：49-52

4 李铁洪,吴华金.长直线接小半径曲线公路交通事故成因及预防对策.中国公路学报,2007,20(1)：35-40

5 陈思嘉.汽车转弯时由内轮差引发的交通事故原因建模与分析.数学通报,2013,52(12)：55-57

6 李俊峰,张雄,任格学等.理论力学.北京：清华大学出版社, 2001

7 唐恒望.内轮差数学建模. 百度文库,2007 http：//wenku. baidu.com/link?url=xEHJoIba1dvqiTfQ4gXrx5PtapBR0i Y1r8-dxFhCkdEkJfrkmtkrlwWlNWNmRTHaF3HOtgy4 W1gMgGpCqon6PbGUmV4OZ6SLfX5i6ljWw1G.

8 范朔.车辆内轮差问题的优化分析.科技世界,2016,9：31-34

9 万禄义.公交车“内轮差”，不容忽视.人民公交,2012,(1)：71

10 后桥转向系统.保时捷(中国),2016.http：//www.porsche.com/ china/zh/models/panamera/panamera-4s/drive-chassis/rearaxle-steering/.

(责任编辑：胡 漫)

O311

A

10.6052/1000-0879-16-263

本文于2016-08-15收到.

1)国家自然科学基金资助项目(11372163).

2)E-mail：qxm@tsinghua.edu.cn

李逸良,邱信明.车辆转弯时内轮差的运动学理论模型.力学与实践,2017,39(1)：94-99

Li Yiliang,Qiu Xinming.A kinematical analysis model of the inner wheel dif f erence.Mechanics in Engineering,2017, 39(1)：94-99