斜拉杆角度变化如何影响杆端位移与杆内力

祝恩阳

(北方工业大学土木工程学院，北京100144)

斜拉杆角度变化如何影响杆端位移与杆内力

祝恩阳1)

(北方工业大学土木工程学院，北京100144)

题目：图1所示为一初始长度为L0，顶端固定铰支，底端竖向滑动铰支的杆件AB.若在B端施加一竖向力F，则B端会向下产生δ的位移，不计杆件自重，求F与δ关系.(此题改编自：北京科技大学、东北大学编著《工程力学(材料力学部分)》第42页例1-10)

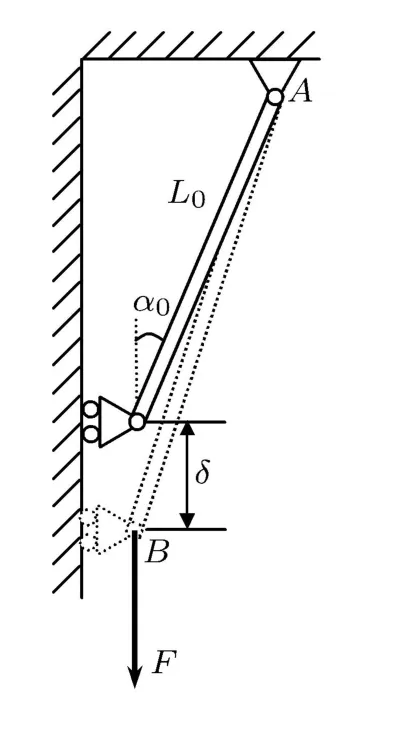
图1

解法 1：在力F作用下，杆件由L0被拉长至L，杆件与竖向夹角α0变为α.变形过程中，满足变形协调条件：Lsinα=L0sinα0.位移δ表示为：δ=Lcosα-L0cosα0.若杆件弹性模量为E，横截面积为A，则拉力F与位移δ成非线性关系

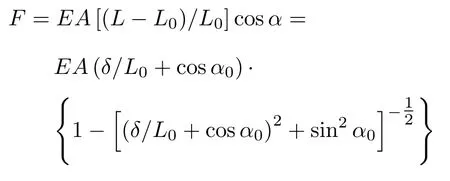
杆件AB变形过程中L与α均发生变化，导致F与δ成非线性关系.

解法 2：教材[1]中忽略角度α的改变，近似认为F与δ是线性关系，利用应变能求解得到：F=EAcos2α0(δ/L0).

比较解法1与解法2，求解的差异在于是否考虑角度α改变的影响.

讨论：当(δ/L0)→0时，解法1与解法2对F的结果一致.这表明在小变形情况下，两种解法均是可靠的.那么，角度α改变对F和δ的影响是怎样的？杆件变形过程中L和α对F的影响可由微分表达dF=(EA/L0)[cosα·dL-(L-L0)sinα·dα]得到. 利用变形协调条件，该微分表达中 dα项与dL项之比为[(L-L0)/L]tan2α，是一个小量，变形较小时，α的改变可忽略.类似地，杆件变形过程中L和α对δ的影响可由微分表达 dδ= cosα·dL-Lsinα·dα得到，dα项与 dL项之比为tan2α，不再是一个小量，α的改变不可忽略.

1 北京科技大学，东北大学.工程力学(材料力学部分).北京：高等教育出版社，2015

10.6052/1000-0879-15-278

(责任编辑：胡 漫)

2015-10-19收到第1稿，2015-11-02收到修改稿.

1)E-mail：zhuenyang@ncut.edu.cn

祝恩阳.斜拉杆角度变化如何影响杆端位移与杆内力.力学与实践,2017,39(1)：88

Zhu Enyang.How are the displacement at the end of a bar and the internal force in the bar inf l uenced by the angle between the bar and the horizontal plane.Mechanics in Engineering,2017,39(1)：88