洛伦兹变换的几何导出1)

邓魁英 楚天广

∗(河北大学工程力学系,河北保定071002)†(北京大学工学院,北京100871)

洛伦兹变换的几何导出1)

邓魁英∗,2)楚天广†,3)

∗(河北大学工程力学系,河北保定071002)†(北京大学工学院,北京100871)

狭义相对论是牛顿力学的重要发展,因其概念抽象,国内力学专业的教学中鲜有涉及.洛伦兹变换在相对论力学中处于核心地位,由其可导出相对论运动学的全部重要结论.本文首先介绍洛伦兹变换的一种典型的代数导出方式,然后利用闵可夫斯基时空图以完全几何的方式给出一种不同的更为直观的导出方式.希望能以一种简洁明了的方式引导力学专业的学生学习狭义相对论.

相对论,洛伦兹变换,闵可夫斯基时空图,经典力学

力学是处理宏观物体运动问题的一门学科,它包括爱因斯坦相对论 (theory of relativity)[1].狭义相对论是牛顿力学在高速运动极限的发展,是现代物理理论的基石[2-3],欧美的经典力学教材中一般都会讲解[4],但国内力学专业的教学中鲜有涉及,一定程度上与相对论的主要概念比较抽象、与直觉相悖、难于教学等因素有关.洛伦兹变换在相对论力学中处于核心地位,可以通过多种途径导出[4-9].本文首先介绍了洛伦兹变换的一种典型的代数导出方式,然后利用闵可夫斯基时空图以完全几何的方式给出一种不同的更为直观的导出方式.这两种导出方式简洁明了,且互为补充,本文旨在由此引导力学专业的学生学习狭义相对论.

狭义相对论的出发点是相对性原理和光速不变原理两条基本假定.相对性原理即假定一切物理定律在所有惯性参考系中具有形式不变性,与观测者的运动速度无关.光速不变原理即假定光子在真空中以恒定速率c传播,与观测者的运动速度无关.由这两条基本假定即可导出洛伦兹变换,进而导出诸如动尺收缩、动钟变慢、质速关系及质能关系等相对论力学的全部重要结论.在低速运动时,洛伦兹变换可用伽利略变换来近似,相对论力学可用牛顿力学来近似[2-5].

现给定任意两个惯性参考系S(x,ct) 和S′(x′,ct′),并假定空间轴x和x′的正方向一致.惯性系S′相对于惯性系S以速率u沿空间轴x的正方向做匀速直线运动,且当t=t′=0时,x=x′=0.同一事件在两个惯性系S和S′中可以分别表示为E(xE,ctE)和E(x′E,ct′E),在下文中非特指某一事件时将省略下标.

根据相对性原理假定,若任意一个事件E(x,ct)在惯性系S中做匀速直线运动,则同一事件E(x′,ct′)在惯性系S′中仍做匀速直线运动,故二者之间存在线性映射关系

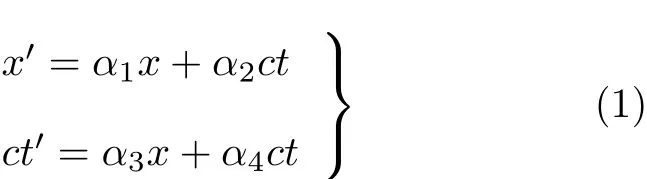
由于惯性系S′相对于惯性系S以速率u做匀速直线运动,也即式(1)定义的线性映射将x=ut映射为x′=0,代入式 (1)中的第 1式可得α2=-α1u/c.重新记α1=γ,且u/c=β(0≤β≤1),则可将式(1)中的第1式表示为

同时,相对于惯性系S′中的观测者,惯性系S以速率u沿空间轴x′的负方向做匀速直线运动,故由式(2)可得

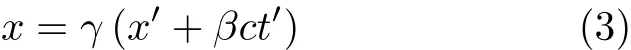
根据光速不变原理假定,光子在惯性系S中的运动轨迹为x=ct,在惯性系S′中的运动轨迹为x′=ct′,二者互为映射,分别代入式(2)和式(3)得

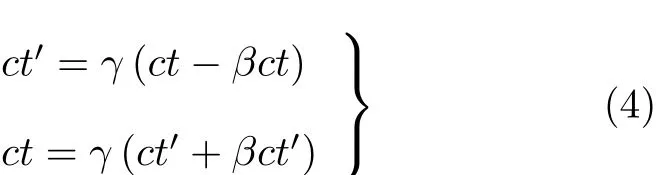
将式(4)中的第1式代入第2式,且空间轴x和x′的正方向一致这一条件决定了γ不能取负值,于是得到

文献中通常将γ称为膨胀系数[2].

再将式(2)代入式(3),并考虑到式(5)给出的γ与β之间的关系式,可以直接导出

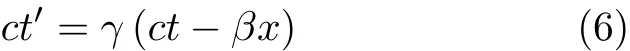
也即在式(1)的第2式中α3=-γβ,α4=γ.

至此,将式(5)代入式(2)和式(6),便得到了以速率u做相对运动的两个惯性参考系S(x,ct)和S′(x′,ct′)之间的线性映射关系式

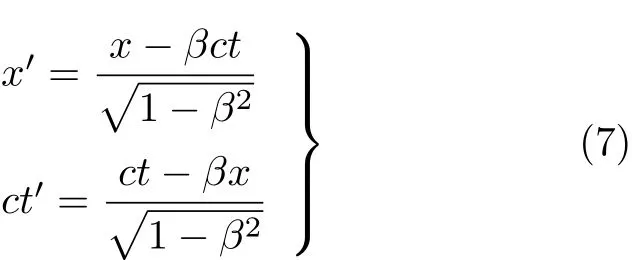
这就是洛伦兹变换(Lorentz transformation),其中β为惯性系S′相对于惯性系S的运动速率u与光速c之比.在式 (7)的变换式中,惯性参考系S(x,ct)的空间轴x与时间轴ct处于完全对称的位置.当u≪c时,式(7)可用伽利略相对性变换来近似,即

此时,惯性系S的空间轴x与时间轴t的位置就不再具有对称性了.

由式(7)中的第2式和式(8)中的第2式可知,相对论力学相对于牛顿力学的革新,关键在于不再采用绝对同时性假定,而假定同时(simultaneity)也具有相对性,即对于在一个惯性参考系中不同地点同时发生的两个事件,在另一个做相对运动的惯性参考系中观测,二者就不再是同时发生的了.

由式(7)的洛伦兹变换可知,在两个惯性系S和S′中分别观测同一事件E时,其时空坐标满足条件

此式蕴含着相对论时空的一个重要不变量,即闵可夫斯基距离测度.欧氏空间中的距离测度在相对论时空中不再适用.另外,式(7)的雅各比行列式的值等于1,即

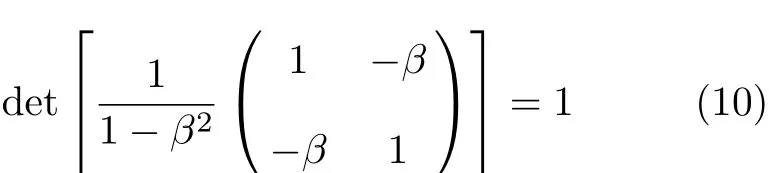
也即做相对运动的两个惯性参考系之间的洛伦兹变换是保面积的.

由式(7)可知,洛伦兹变换将惯性系S中的运动轨迹x=βct和ct=βx分别映射为惯性系S′中的x′=0和ct′=0.若将惯性参考系S(x,ct)的空间轴x和时间轴ct用平面内的两条互相垂直的坐标轴来表示,则光子的运动轨迹沿着各象限的角平分线,而惯性参考系S′(x′,ct′)的空间轴x′=0和时间轴ct′=0则关于光子的运动轨迹对称.此即为闵可夫斯基时空图(图1).

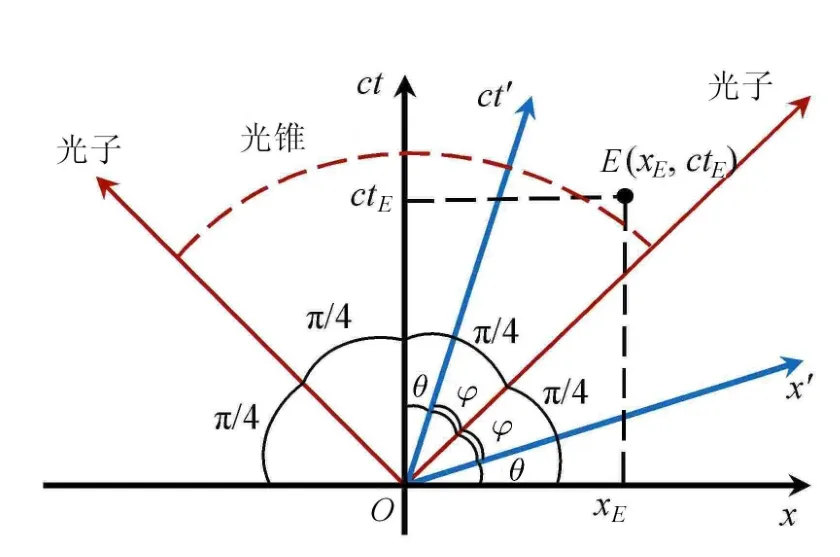
图1 闵可夫斯基时空图与光锥

在闵可夫斯基时空图中,因果律决定了可能事件E(xE,ctE)只能发生在以光子的运动轨迹为边界且以ct为轴的光锥内(图1).匀速直线运动的轨迹是位于光锥内的一条直线,如惯性系S′的时间轴ct′即为在惯性系S中观测到的惯性系S′的运动轨迹.

闵可夫斯基时空图为相对论运动学的讨论提供了一种非常直观简明的方式.但就我们所知,文献中尚未见到如何从闵可夫斯基时空图出发利用几何方式导出式(7)中的洛伦兹变换,此即为我们在下文中的主要工作.

在图2所示的闵可夫斯基时空图中,惯性系S的空间轴x和时间轴ct互相垂直,作菱形OADB.在图3所示的闵可夫斯基时空图中,惯性系S′的空间轴x′和时间轴ct′互相垂直,则菱形OADB相应变换为正方形O′A′D′B′.那么,图2中等腰三角形OAD内的任意一个事件E(xE,ctE)总与图3中等腰直角三角形O′A′D′中的一个事件E(x′E,ct′E)对应,故可认为二者的面积相等,表示为

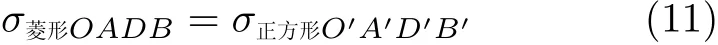
也即假定惯性参考系S(x,ct)和S′(x′,ct′)之间的线性变换是保面积的.这是我们以几何方式导出洛伦兹变换的出发点.

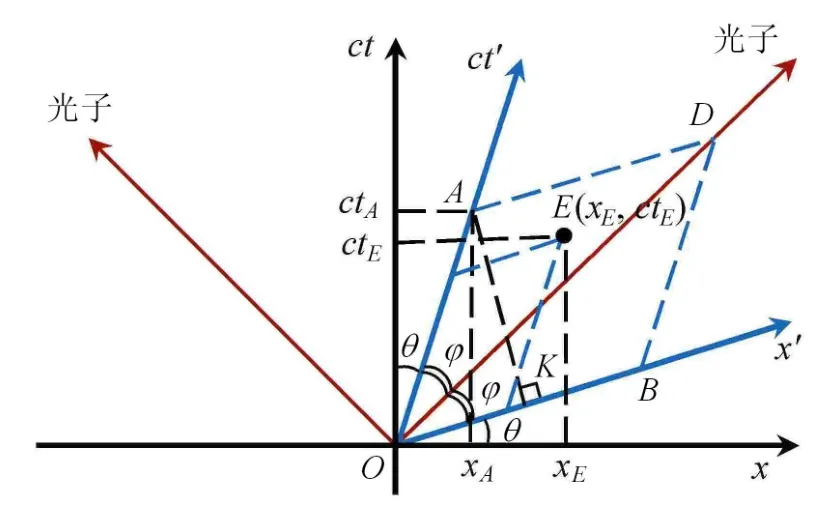
图2 闵可夫斯基时空图与菱形OADB

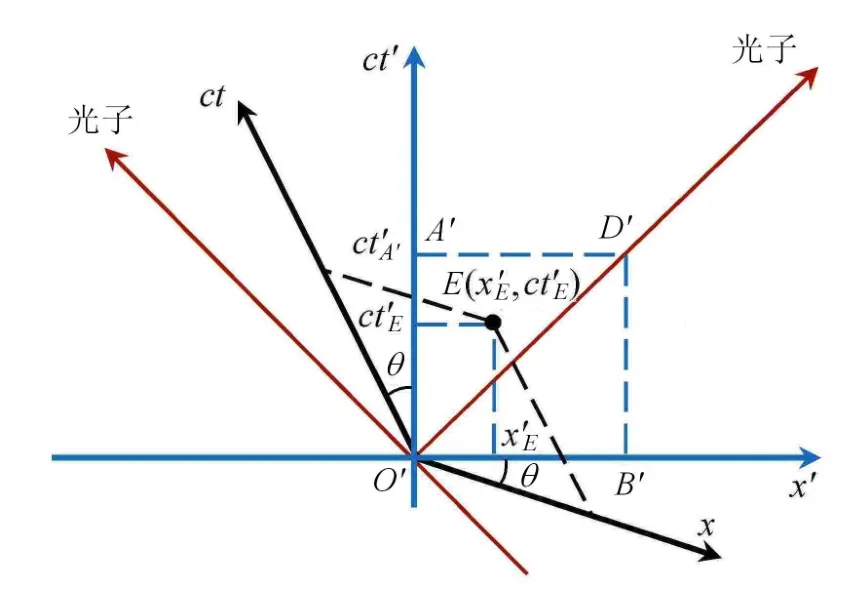
图3 闵可夫斯基时空图与正方形O′A′D′B′

在图2所示的闵可夫斯基时空图中,作AK垂直于OB,则菱形OADB的面积

设事件A在惯性系S中可以表示为A(xA,ctA),则由图2中的几何关系及运动学关系xA=utA显然可得

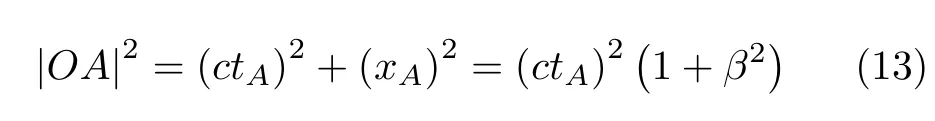
和

再由式(14)通过三角关系可得

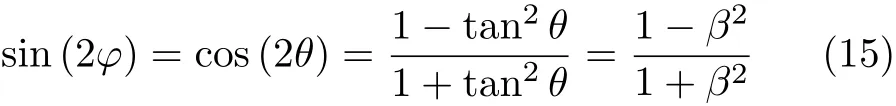
将式(13)和式(15)代入式(12)中,得到在图2所示的闵可夫斯基时空图中菱形OADB的面积

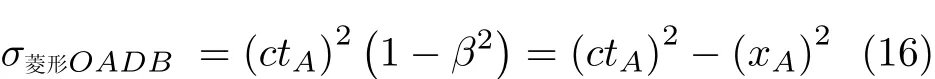
而在图 3所示的闵可夫斯基时空图中,正方形O′A′D′B′的面积显然为

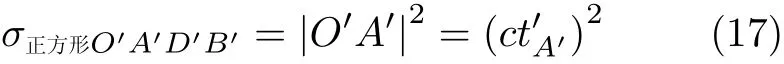
于是由式(11)可知

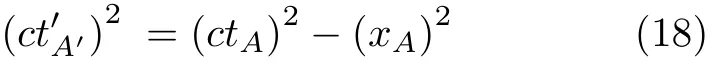
此式对于在惯性系S′中观测时静止于原点O′处的任意事件A′(0,ct′A′)均成立,也即式 (18)为式 (9)的特例.从由式(12)导出式(18)的过程我们可以非常直观地看出,式(9)中的闵可夫斯基距离测度与式(10)中洛仑兹变换的保面积性是完全等价的.

设事件E在惯性系S和S′中可以分别表示为E(x,ct)和E(x′,ct′).由图4可知,惯性系S′中的同时线EA与惯性系S中的空间轴x的夹角也为θ,并注意到运动学关系xA=utA,则

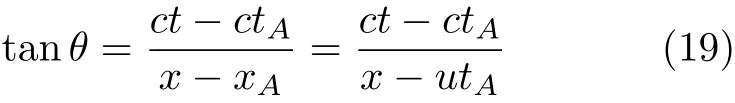
结合式(14)中已知的关系式tanθ=β,可以解得

又由式(18)及xA=utA可知

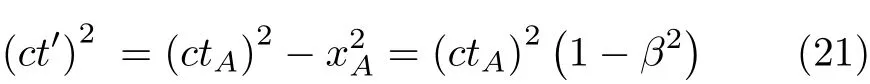
将式(20)代入式(21),便导出了

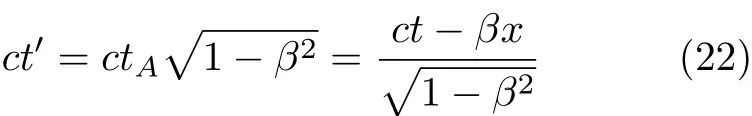
此即为式(7)中洛伦兹变换的第2式.

图4 闵可夫斯基时空图与事件E

再注意到图4中惯性系S′中的同地线EG与惯性系S中的时间轴ct的夹角也为θ,由几何关系还可知

于是有

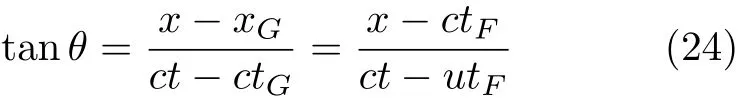
同样结合式(14)中的tanθ=β,可以得到

又由式(18)及运动学关系xF=utF可得

将式(25)代入式(26),便导出了

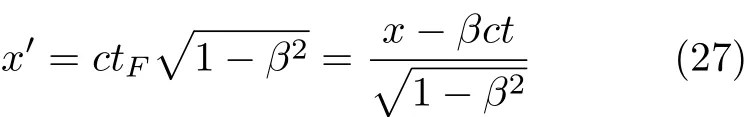
此即为式(7)中洛伦兹变换的第1式.

至此,我们便通过几何的方式导出了由式 (22)和式(27)表示的洛伦兹变换,其中起关键作用的是式(18)蕴含的相对论时空中的闵可夫斯基距离测度.

由图4可知,事件E(x,ct)在惯性系S中的速率为v=x/t,同一事件E(x′,ct′)在惯性系S′中的速率为v′=x′/t′.将式(27)与式(22)相比可得

再将u/c=β代入其中即可得

此即为相对论运动学中同一事件在不同惯性参考系中运动速率之间的关系式.当u≪c时,式(29)即可用牛顿力学中同一动点在不同惯性参考系中运动速率之间的关系式来近似,即

由式(29)可知,当v=c时,v′=c,即光子在所有惯性参考系中的速率保持不变,这就是作为狭义相对论出发点的两个基本假设之一.值得一提的是,不少工作指出,光速不变原理假定对于导出洛伦兹变换并不是必要的[6-9].任何非伽利略时空线性变换必然要求存在一个速率上限,以此为基础导出的广义洛伦兹变换使得相对论的理论基础更为稳固,即使将来发现超光速粒子的存在,相对论中以光速不变原理假定为前提导出的相关结论经适当调整后仍然成立[8-9].

洛伦兹变换在狭义相对论中处于核心地位,可用其将相对性原理假定更具体地表述为：一切物理定律的方程式在洛伦兹变换下具有形式不变性[2].由洛伦兹变换出发,便可导出诸如动尺收缩、动钟变慢、质速关系及质能关系等相对论力学的全部重要结论.同样也可以利用闵可夫斯基时空图从几何的角度为这些重要结论给出更为直观的解释[10].

从本文以几何方式导出洛伦兹变换的过程可以清楚地看出,狭义相对论仍然假定空间是平直、均匀和各向同性的,时间是均匀流逝的,而牛顿力学是相对论力学在低速运动极限的近似.但牛顿万有引力公式在洛伦兹变换下不具有形式不变性,爱因斯坦为解决这个困难建立起来的广义相对论则是一种弯曲时空引力理论[3-5],该理论预言的引力波(gravitational waves)于整整100年后的2015年9月14日第一次被科学家直接探测到[11].

综上所述,本文利用闵可夫斯基时空图从几何的角度导出了洛伦兹变换,与其代数导出互为补充,有利于学习者从更直观的角度理解狭义相对论的平直时空假定和非欧距离测度等概念,以及相对论力学相对于牛顿力学的关键革新,即不再采用绝对同时性假定,而是利用光速不变性定义了同时的相对性.本文在导出洛伦兹变换的过程中只应用了基本的线性代数和平面几何知识,希望能以这种简洁明了的方式引导力学专业的学生学习狭义相对论.

1 钱学森．我对今日力学的认识．力学与实践,1995,17(4)：1-1

2 张元仲．从牛顿力学到狭义相对论．力学与实践,2005,27(4)：1-7

3 张元仲．广义相对论的产生与发展．力学进展,2002,32(4)：495-504

4 Goldstein H,Poole C.Safko G.Classical Mechanics(3rd edn).San Francisco：Addison-Wesley,2001

5 Einstein A.Relativity：The Special and the General Theory.New York：Pi Press,2005

6 Dunstan DJ.Derivation of special relativity from Maxwell and Newton.Phil Trans R Soc A,2008,366：1861-1865

7 Levy-Leblond JM.One more derivation of the Lorentz transformation.Am J Phys,1976,44：271-277

8 Lee AR,Kalotas TM.Lorentz transformations from the fi rst postulate.Am J Phys,1975,43：434-437

9 戴又善．狭义相对论与运动速度上限．北京大学学报(自然科学版),2013,49(3)：356-364

10 杨志万．闵氏时空图在相对论教学中的应用．大学物理,2016, 35(2)：27-29

11 Abbott BP,et al.Observation of gravitational waves from a binary black hole merger.Phys Rev Lett,2016,116：061102

(责任编辑：胡 漫)

O412.1

A

10.6052/1000-0879-16-125

2016-04-13收到第1稿，2016-06-05收到修改稿.

1)河北大学优秀博士引进人才项目(2014-304)和国家“973计划”项目(2012CB821200)资助.

2)邓魁英，博士，副教授，主要研究方向为复杂系统动力学与控制.E-mail：RossDeng@pku.edu.cn

3)楚天广，博士，教授，主要研究方向为复杂系统动力学与控制.E-mail：chutg@pku.edu.cn

邓魁英,楚天广.洛伦兹变换的几何导出.力学与实践,2017,39(1)：82-86

Deng Kuiying,Chu Tianguang.Geometric derivation of the Lorentz transformation.Mechanics in Engineering,2017, 39(1)：82-86