大型飞机气动载荷向有限元节点等效分配的方法

张建刚 孙仁俊 唐长红

(中国航空工业集团公司第一飞机设计研究院，西安710089)

大型飞机气动载荷向有限元节点等效分配的方法

张建刚1)孙仁俊 唐长红

(中国航空工业集团公司第一飞机设计研究院，西安710089)

将气动载荷分配到有限元节点上是工程实际中的一项重要而繁琐的工作.对于二维的翼面气动载荷，根据原始的气动压力点的压力值，采用样条曲面拟合的方法，拟合得到翼面压力分布曲面，由该曲面得到有限元节点上的压力值，再在有限元模型单元上积分得到有限元节点载荷供强度设计使用.大型飞机具有复杂的增升装置，增升装置的气动载荷可能是三维的，对于三维的翼面载荷，直接在气动网格上积分得到气动载荷的小块集中力，然后按照沿某一方向投影的方法，找到该集中力作用的单元，最后按照二次规划的方法，将其分配到有限元节点上.

气动载荷,有限元节点,薄板样条

在飞机的结构强度设计中，气动载荷是非常重要的设计输入.在国内的航空院所里，气动载荷由载荷专业计算，结构强度专业将该载荷施加在有限元模型上作为输入进行下一步的设计.为了确保载荷输入的准确性，一方面载荷专业要努力使其计算结果更准确，另一方面，强度专业也要确保将气动载荷正确地施加在计算模型上.在工程中，将气动载荷等效分配到有限元节点上，是一项非常繁琐但又很重要的工作.而目前航空航天行业广泛使用的强度计算软件如MSC.Patran/Nastran,Abaqus等，对于不均匀面载荷加载还不能自动实现.如果人工手动地对节点进行加载，满足不了工程实际的要求，因为实际的有限元模型具有大量的节点和工况.为了解决这一难题，出现了很多的算法.

国外相关研究常见于气动弹性专业计算，气弹计算每一迭代步需要将气动载荷施加在结构节点上：首先在气动网格上积分得到气动载荷集中力，然后根据虚功原理，用样条插值矩阵将空气动力网格上的气动力变换为结构网格点上的等效值[1-3].目前国内航空领域常用的算法是“多点排”方法[4]，该方法以应变能最小及静力等效为约束条件，将每一个气动载荷分配到若干个有限元节点上.王专利[5]、徐建新等[6]通过计算证明了该方法的正确性.高尚君等[7]提出了基于弹簧-悬臂梁模型最小变形能的气动载荷分配方法，解决了气动点与部分有限元点重合而导致的难以求解的问题.这些算法能有效解决工程实际中的一些问题，但也还存在着需要改进的地方.首先，载荷分配的起点是积分后气动载荷的集中力.现代大型飞机翼面结构复杂，气动分区和结构分区往往不一致，直接在气动网格上积分成集中载荷有可能会跨区域传递载荷，导致传力路线不真实；其次,这些方法分配载荷时人为地指定了一些节点去分配相应的气动载荷，也可能导致传力路线的不真实，实际上应该充分利用有限元模型的单元和节点信息，遵循就近分配的原则以保证载荷传递的正确；最后，分配的载荷都假设为二维载荷，这对翼面盒段等扁平结构是适用的，但对现代大型飞机的增升装置及整流罩、雷达罩等三维气动面则显得较为牵强.

现代的大型飞机，比如大型运输机，为了良好的气动及起降性能，大多都布置有前缘缝翼、后缘多缝襟翼等复杂的增升装置.这些装置导致了大型飞机的气动载荷分布极为复杂，并且这些翼面本身的结构也较为复杂，传力路径复杂.强度设计专业必须保证将这些气动载荷以最小的代价，真实、准确地施加到结构有限元模型上，这是强度设计的首要条件，也是飞机精细化设计的必然要求.

本文以工程实际需要为出发点，研究了如何准确、快速地将气动载荷分配至有限元节点上，以供同行借鉴参考.

1 气动载荷的提供形式及翼面结构的分类

载荷专业给出的气动载荷一般形式是：根据试验或理论计算给出一系列离散点上的压力分布及翼面的总载、总矩.这些压力点和有限元模型节点是不重合的.

根据翼面的结构及其受力特点，可以将其大致分为两类：一类是翼面盒段等比较扁平的结构，这类结构主要承受垂直于弦平面的气动载荷，另外两个方向上的气动载荷相比而言都是小量，并且在这两个方向上翼面的刚度又很大，因此可以忽略掉这两个方向的气动载荷而不会引入较大的误差，因此可认为这一类翼面载荷的分布是沿展向和弦向的二维分布.另一类是前缘缝翼、后缘襟翼等曲率较大的翼面，这类翼面有两个以上方向的载荷具有相同的数量级，因此不能忽略任何一个分量，必须按照空间分布的三维载荷来对待.并且这类翼面上的气动载荷变化梯度大，给出的气动载荷的网格较二维的更为细密.

本文使用的载荷分配的基本思想是：对于二维载荷，根据已知气动点上的压力值，通过薄板样条插值函数，拟合出压力分布曲面，由该曲面得到每一个有限元节点上的压力值，再在单元上对压力进行积分，得到有限元节点上的载荷.插值方法采用航空航天工程中广泛使用的薄板样条曲面插值.对于三维载荷，直接在气动网格上进行积分得到集中力，然后遵照就近分配的原则分配到有限元模型上.

2 薄板样条插值函数

在分配载荷之前需要由气动点的压力值求出有限元节点上的压力值，本文采用薄板样条插值函数[8].设在N维欧氏空间内域D上有n个向量(每个向量代表一个节点坐标)及其对应的函数值，即已知

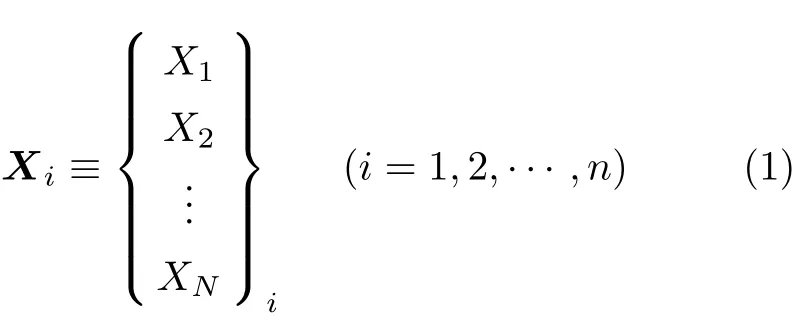
设向量X的函数W=W(X)(称为真实函数)是单值连续的，则对D上的任一向量Xk(称为插值点)来说，必有一个且只有一个确定的函数Wk与之对应.由于在插值问题中真实函数是不知道的，任一向量Xk所对应的函数值无法直接求出.为此，必须利用已知条件(节点信息)构成一个逼近函数，用它来代替真实函数，借以计算任一向量Xk所对应的函数之近似值.在这里，逼近函数的形式如下

式(2)中的待定系数由无穷远处的边界条件及n个已知节点函数值来确定

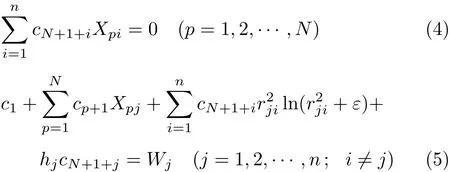
将上述方程组写成矩阵形式如下

记为

式中S为待定系数组成的向量；f为已知函数值和0组成的向量；bji=r2jiln(r2ji+ε)；m=N+1+n.

式(6)是一个线性代数方程组，对其求解即可得到式(2)中的各待定系数，进而得到逼近函数.对于任一待求节点，将节点坐标代入式 (2)即可求得对应的函数值.

3 二维载荷的分配方法

二维载荷分配方法适用于机翼盒段等扁平翼面，载荷方向垂直于机翼的弦平面.气动专业提供的载荷压力分布是一系列离散点上的压力，这里的压力指的是当地静压减去来流静压后的剩余量，也就是压力系数和速压的乘积.在式(6)中，令N=2，根据气动点的坐标构造出左边的A矩阵，根据已知点的压力值构造向量f，求解方程得到向量S，代入式(2)后得到有限元点上的压力值.图1给出了某机翼的已知压力值和插值得到的压力值的比较.图中的x和y坐标是沿着机翼展向和弦向的坐标，z坐标是压力.

由图1可以看出，插值后的压力曲面和插值前的压力曲面吻合程度很好，可以由有限元节点上的压力积分得到节点的集中力.分配气动载荷的单元一般是模型表面的单元，大多数是四边形单元，还有少量的三角形单元.对于三角形单元，3个节点坐标

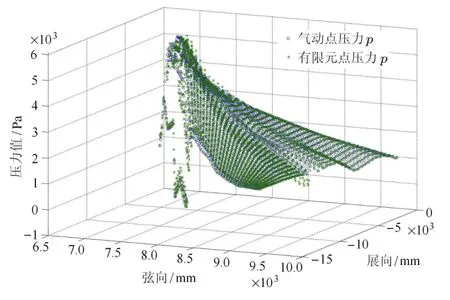
图1 气动点上的压力值和插值后有限元点上的压力值

为(xi,yi),i=1,2,3,假设压力分布在单元上呈平面分布，即

根据已知节点的压力值即可求出式(8)中的常数A,B和C.

假设三角形三个节点上分到的载荷是fi,i= 1,2,3，则有

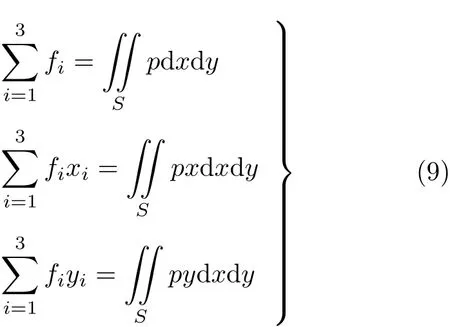
式(9)中的积分区域S是三角形的表面，经过推导可以得到

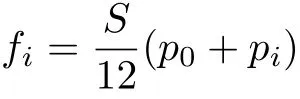
式中，p0=p1+p2+p3,p1,p2和p3是三角形三个节点上的压力值；S为三角形面积.

由以上方程组即可求解得到三角形节点的集中载荷.四边形单元可以化为两个三角形单元，再做如上的处理.

4 三维载荷的分配方法

三维载荷的分配方法理论上可以和二维的处理方法类似，即根据已知点的压力值采用薄板样条函数插值出有限元节点处的压力值，然后在单元上积分即可得到集中载荷.但是在工程实际中，承受三维载荷的翼面往往压力梯度较大，气动网格密集，相比二维载荷,气动点的数目大为增加.一块翼面往往布置有上万个气动点，这时如果仍然进行插值运算，会导致计算量急剧增大.在个人计算机上求解一个工况的时间以小时计，实际的工况数又成百上千，这种做法在工程实际中不现实.如果在气动点上挑选一部分点插值，无形中又会降低载荷的精度.

为了解决这一问题，权衡利弊后采用如下做法：在气动网格上直接积分得到气动单元上的小块集中力，再将这些力等效到有限元节点上.有了小块集中力之后，向有限元节点等效分配载荷之前需要先准确找到该力作用的单元.一个简便可行的方是：沿着某一个方向(一般可选气动单元平面法向量绝对值最大的分量方向)，将集中载荷的作用点向翼面结构投影，找到分配载荷的单元.假设沿着z向投影，某一个四边形单元的4个节点坐标为(xi,yi),i=1,2,3,4，则集中力作用点在四边形投影坐标为(x,y)，如图2所示.

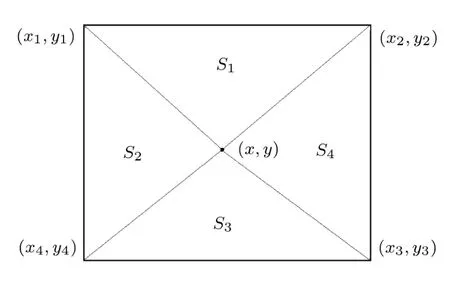
图2 集中力作用点向四边形投影示意图

假设四边形面积是S，载荷作用点的投影点和四边形4个节点连成4个三角形，若则认为载荷点投影到了四边形单元内部，则应该将该集中载荷分到这个四边形的节点上.三角形投影方法类似.

将集中载荷分配到三角形单元可以按照静力等效原则直接分配.对于四边形单元，因为约束方程的个数少于自变量的个数，存在多种解.根据应变能最小原理，应变能近似正比于4个力的平方和，可以按照优化理论中的二次规划方法进行分配.比如需要分配z方向的气动载荷Fz，载荷作用点坐标是(X,Y)，假设四边形4个节点分配到的载荷和节点坐标分别为fzi和(xi,yi)，i=1,2,3,4，则问题等效为以下二次规划问题[9]

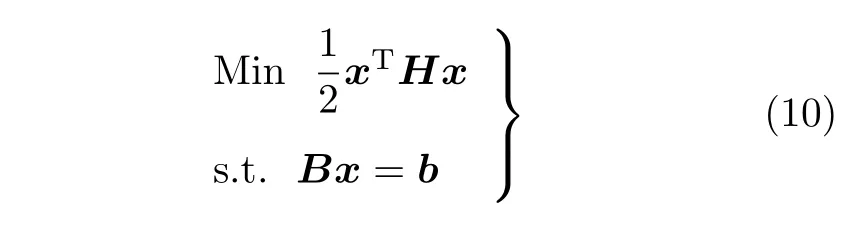
其中，H是4阶单位矩阵

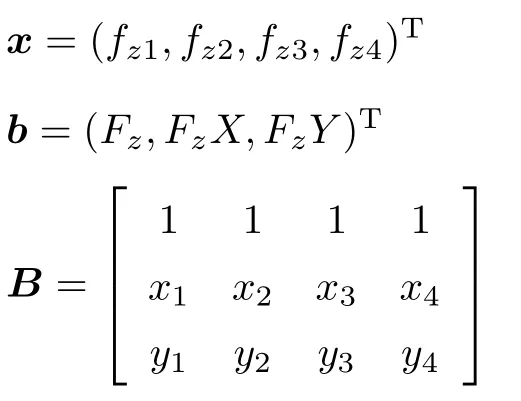
式 (10)中的目标函数的意义是 4个力的平方和最小.首先定义Lagrange函数

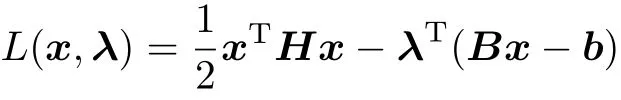
令∇xL(x,λ)=0及∇λL(x,λ)=0.

由此得到方程组

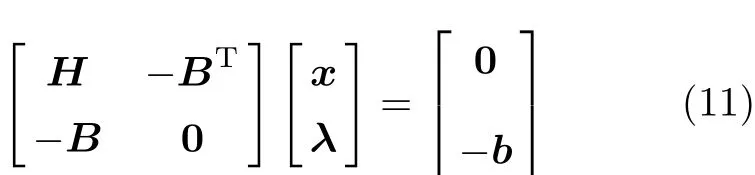
求解式(11)即可得到各个节点上分配到的z方向的载荷.x和y方向的载荷分配方法完全相同.图3～图5是按照以上方法分配的几个飞机部件的载荷.

图3 某大型运输机前缘缝翼载荷分配结果

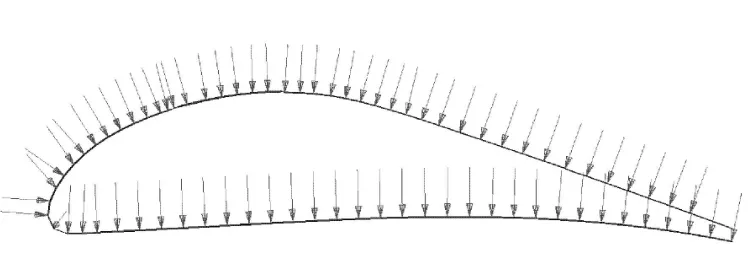
图4 某大型运输机后缘襟翼载荷分配结果

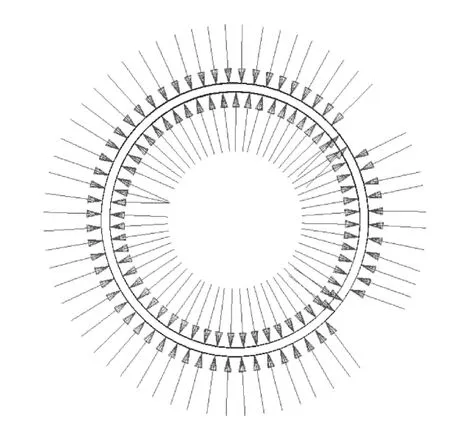
图5 某飞机喷管载荷分配结果

5 结论

(1)根据以往的工程应用的实际情况，二维载荷按照以上做法求得的整个翼面的总载荷可能和气动专业测力测矩得到的结果略有差异，对于大的载荷工况(往往是翼面本身的设计情况)误差一般在1%以内；对于小载荷工况(这些工况可能是别的部件的设计情况，为了全机平衡，该翼面上的载荷可能是配平载荷，非翼面本身的设计情况)，误差略大一些，最大不超过5%.为了保证全机求解时的平衡，可将上述载荷按线性化略加修正即可.

(2)对于三维载荷，按照该方法处理后，气动载荷基本上垂直于当地翼面，如果有限元网格和气动网格的疏密程度及外形、边界完全一致，则处理后的气动载荷完全垂直于翼面，这也证明了方法的正确性.

(3)该方法数学理论清晰，编程简单.通过以往工程型号的验证，证明可以有效地解决工程实际中的问题.

1 Prananta BB,Veul RPG,Boelens OJ.Manoeuvre-loads computations using CFD-based static aeroelastic simulations for multiple store conf i gurations.27th International Congress of the Aeronautical Sciences,Nice,France,2010

2 Johannes KSD,Mostafa MA,Yasser MM,et al.Static aeroelastic stif f ness optimization of a forward swept composite wing with CFD correct aero loads.International Forum on Aeroelasticity and Structural Dynamic,Saint Petersburg Russia,2015

3 Rodden WP,Johnson EH.MacNeal-Schwendler Corporation. MSC.Nastran Version 68,Aeroelastic Analysis’s Guide.MacNeal-Schwendler Corp,Santa Ana,CA,2004

4 解思适.飞机设计手册第9册载荷、强度和刚度.北京：航空工业出版社，2001

5 王专利.翼面结构有限元模型节点气动载荷计算.洪都科技，2007,(1)：7-14

6 徐建新,王彪.方向舵静强度试验载荷等效计算研究.装备制造技术，2013,(1)：14-16

7 高尚君，于哲峰，汪海.基于弹簧-悬臂梁模型最小变形能的气动载荷分配方法.飞机设计，2013，(6)：1-4

8 赵永辉.气动弹性力学与控制.北京：科学出版社，2007

9 蒋宝林.优化理论与应用.北京：清华大学出版社,2006

(责任编辑：刘希国)

THE METHOD OF TRANSFERRING AERODYNAMIC LOAD TO FEM
NODES FOR LARGE AIRPLANE

ZHANG Jiangang1)SUN Renjun TANG Changhong
(The First Aircraft Institute of the Aviation Industry Corporation of China，Xi’an 710089，China)

Transferring the aerodynamic load to FEM(f i nite element method)nodes is a hard work but is very important.In order to transfer the two-dimensional aerodynamic load,a thin plate spline surface of the pressure is constructed according to the existing pressure on the aerodynamic nodes.Then the pressure on the FEM nodes can be computed.At last the concentrated force on the FEM Nodes can be obtained by integration of the pressure on the FEM elements.The large airplane often has complicated high-lift devices and their aerodynamic load may be three-dimensional.For the three-dimensional aerodynamic load,with the integration of the pressure on the aerodynamic webs,the concentrated force on the aerodynamic nodes can be obtained, and these forces can be transferred to the FEM nodes using the quadratic program method.

aerodynamic load,FEM(f i nite element method)nodes,thin plate spline

V211.41

A

10.6052/1000-0879-16-170

2016-05-13收到第1稿，2016-07-18收到修改稿.

1)张建刚，硕士，高级工程师，主要从事飞机强度及载荷设计.E-mail：155246438@qq.com

张建刚,孙仁俊,唐长红.大型飞机气动载荷向有限元节点等效分配的方法.力学与实践,2017,39(1)：25-29

Zhang Jiangang,Sun Renjun,Tang Changhong.The method of transferring aerodynamic load to FEM nodes for large airplane.Mechanics in Engineering,2017,39(1)：25-29