近断层地震作用下钢筋混凝土连续梁桥地震易损性分析1)

刘 强 王妙芳 严通梅

(集美大学工程技术学院，福建厦门361021)

近断层地震作用下钢筋混凝土连续梁桥地震易损性分析1)

刘 强2)王妙芳 严通梅

(集美大学工程技术学院，福建厦门361021)

考虑桥墩、支座构件及主梁的碰撞损伤指标，对钢筋混凝土连续梁桥进行了地震易损性分析.综合考虑了结构参数的不确定性，从太平洋地震工程研究(Pacif i c earthquake engineering research,PEER)数据库中随机选取了20条近场地震记录，得到大量的随机地震-结构样本.结合不同破坏状态下的桥梁损伤指标，根据结构的能力与需求得到了桥梁各构件及整体桥梁结构的地震易损性曲线.从概率意义上判断在强烈地震作用下桥梁结构所处的破坏状态，为今后在役的同类型桥梁震害预测提供了参考.

钢筋混凝土连续梁桥,近场地震,地震易损性分析,损伤指标,桥墩

近几年，人们注意到，近断层地震动明显的长周期速度和位移脉冲运动可能对隔震建筑或桥梁等长周期结构的抗震性能和设计带来不利影响[1-3].基于性能的桥梁抗震设计理论关注结构在多性能水准下的概率抗震能力，其中增量动力分析方法是近年来发展起来的一种用于评价结构抗震性能的动力参数分析方法[4-5].目前国内外学者对数值分析方法的研究大多集中在对地震烈度或地震动峰值加速度上，没有考虑近、远场地震动选取的不同；也少见同时考虑地震动随机性及结构参数随机性,对结构进行地震易损性分析、抗震性能评估与震害评价的研究[6-7].

中、长跨度的钢筋混凝土连续梁桥在我国高速公路中是比较常见的桥型，且大都在高烈度地震区域大量建设，很可能遭受非平稳特性很强的近断层脉冲地震动作用.历次地震灾害统计资料表明此类桥梁在近断层地震作用下，会发生支座脱落、伸缩缝处的移位和墩梁相对位移过大以及主梁碰撞引发的落梁等较严重的震害问题.为此，本文将结合工程实际，以中、长跨度钢筋混凝土连续梁桥为对象，考虑最易发生破坏的桥墩、支座以及主梁的碰撞构件，对在近场地震作用下桥梁局部损伤构件及整体结构系统进行增量动力分析，分别获得相应的地震易损性曲线.为中、大跨度桥梁结构的抗震性能评估提供理论依据.

1 地震易损性分析方法

结构的地震易损性是指给定地震动某一强度值时，结构的破坏超过某一规定的概率.根据地震易损性的定义，对于桥梁的易损性可以表达为[8]

式中，FR(a)为地震易损性；P[·]为结构的破坏超过某一规定的概率 (失效概率)；EDP为工程需求参数，LS表示某一指定结构破坏状态，IM表示地震动强度系数；fR|IM[r|a]是IM=a时，结构或构件的EDP达到或超过某一指定结构(或构件)破坏状态的条件概率密度(即破坏超越概率).

假定EDP和IM之间服从对数正态分布关系，则结构或构件的需求参数均值为[9]

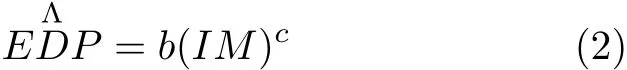
其中，系数b和c为IM和EDP参数回归分析后得到的系数.

进一步计算结构达到或超过破坏状态LS的地震易损性FR(a)，通过统计方法进行曲线拟合，得到光滑的“地震易损性曲线”，其方程的表达式为[10]

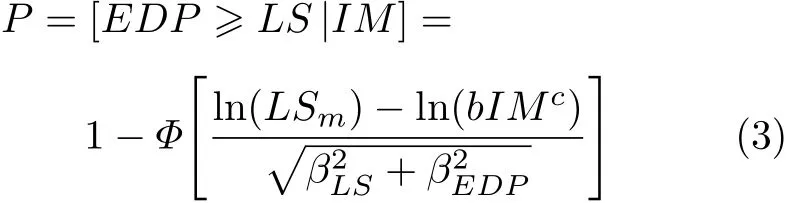
式中Φ为标准正态分布累积密度函数，LSm为破坏状态下的对数正态分布平均值.βLS,βEPD分别为结构能力、需求的对数标准差，本文取βLS=0.6.地震易损性分析可以评估桥梁结构或构件在某一特定的地震烈度作用下，结构遭受损伤状态的概率.

2 桥梁模型及随机地震动-结构样本确定

2.1 桥梁结构模型

本文研究对象为一座六等跨钢筋混凝土连续梁桥，总长度为120m，桥型布置如图1所示.桥梁上部结构为6m×20m现浇混凝土箱型梁，梁高1.3m，采用C40号混凝土.下部结构为钢筋混凝土圆形墩柱，采用C30号混凝土，其中①、⑤号墩为双柱式桥墩，桥墩直径为1.3m，墩高8m，②、③、④号墩为变截面的单柱式桥墩，墩高为8m，直径为1.5m的圆形桥墩.主梁与桥墩墩顶之间采用两种抗震球形支座连接(固定支座与活动支座).在两岸台口设置伸缩缝.桥墩基础材料为C30混凝土.该地区抗震设防烈度为8°，场地类别为Ⅱ类.本文利用OpenSees软件建立桥梁结构的弹塑性有限元动力分析模型，在进行非线性时程计算分析时，仅考虑沿桥纵向地震动输入时结构的地震响应.

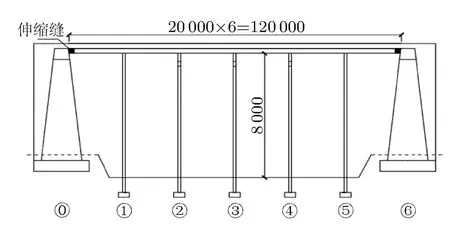
图1 桥梁结构模型

2.2 近场地震记录的选取

目前，地震动输入有人工拟合和实际地震记录两种，但是人工生成的地震动是建立在规范规定的标准反应谱基础之上，仅仅能体现地震动反应谱的均值特性，不能反映地震动的随机性.本文选用实际的近场地震波记录，并考虑地震波输入的随机性，研究资料表明，10～20条地震记录能够达到一定精度.为此本文从太平洋地震工程研究中心新一代地震记录数据库中，根据桥梁所处的场地条件和震级，随机选取断层距小于10km且存在明显速度脉冲效应的近场地震记录20条，其基本特征为：(1)断层距变化范围：0～10km；(2)矩震级变化范围：6.5～6.9；(3)vs30变化范围：260～510m/s；(4)存在明显的速度脉冲.各地震波的加速度反应谱及其均值反应谱见图2.本桥一阶自振周期为0.954s，所选近场地震动记录与均值反应谱吻合较好.

图2 近场地震动反应谱及均值反应谱

2.3 桥梁结构参数敏感性分析及随机地震动-结构样本

本文取固定桥墩(②号墩)为研究对象，以墩底的曲率延性作为评价指标，改变每组的参数，对比不同参数样本与原始模型分析结果的差异，并进行归一化处理，得到了地面运动峰值加速度PGA=1.0g时各结构参数敏感性，如图3所示.从图中可以看出，钢筋屈服强度、上部结构质量、支座摩擦系数、混凝土抗压强度这几个结构参数变量曲线的斜率较大，表明桥梁结构对于地震响应较为敏感.因此采用拉丁超立方抽样法 LHS(Latin hypercube sampling)对4个主要参数进行随机组合形成100个分析的桥梁结构样本.最终，再将桥梁结构样本与选择的地震波记录进行组合生成随机地震-结构分析样本.

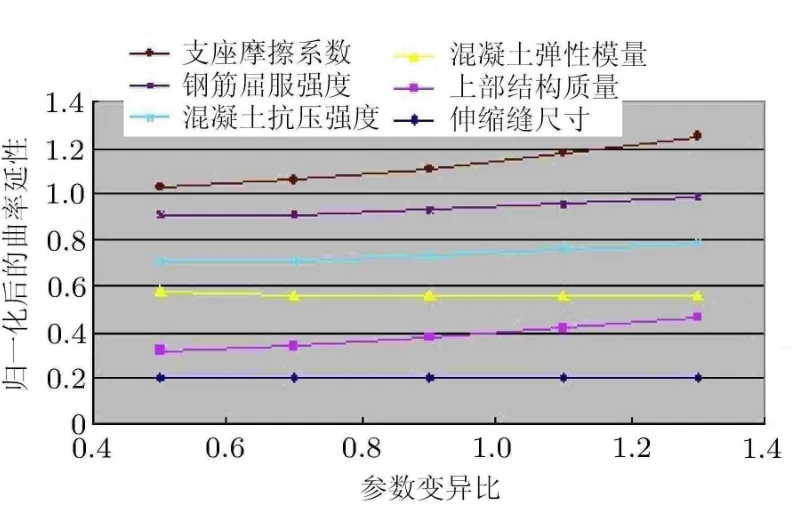
图3 地震动(PGA=1.0g)作用下各结构参数的敏感性

3 桥梁系统结构的地震易损性分析

3.1 损伤指标的确定

本文破坏状态的定义采用灾害损失评估系统HAZUS中定义的方法，将破坏等级分为无损伤、轻微破坏、严重破坏以及倒塌4种，通过截面M-φ关系确定各损伤状态对应的曲率，以此作为评判结构损伤的依据[11-13].为此从桥梁结构的桥墩的破坏，活动支座破坏以及主梁的碰撞三个方面定义桥梁的破坏状态，并以此来确定其相应的损伤指标.

3.1.1 桥墩

不同破坏状态下桥墩的损伤指标可以通过截面的弯矩曲率关系来确定.震害经验也表明，在地震作用下，桥墩底部一般首先失效破坏.因此以桥墩底部截面曲率定义破坏状态，桥墩各级损伤状态及损伤指标描述，如表1所示.

表1 桥墩损伤状态及损伤指标描述

3.1.2 活动支座

对桥梁结构抗震分析表明：固定支座一般能够满足抗震强度要求，而活动支座在强烈地震作用下可能会发生过大位移而导致失稳、主梁下落等破坏.在算例中，支座采用减震球形支座，在顺桥方向设计为活动支座.由于篇幅有限，本文只对(②号)活动支座进行易损性评价.在分析中考虑支座性能的变异性，当墩顶活动支座最大容许位移达到200mm时即认为发生失效，表2给出了不同损伤状态下活动支座变形率的定义.

表2 支座损伤指标描述(单位：mm)

3.1.3 主梁梁端与桥台碰撞

本文假定主梁梁端与桥台之间伸缩缝宽度Gap=100mm，在分析中综合考虑温度的变化以及材料的变异性对伸缩缝宽度的影响，在近断层地震作用下，当主梁梁端相对位移达到或者超过100±10mm时，就认为发生了碰撞.

3.2 桥梁构件易损性分析

通过100个桥梁-地震样本的时程分析，得到构件的最大响应值(桥墩塑性铰最大截面曲率、墩顶支座最大位移、梁端最大位移),然后建立各个极限破坏状态下需求能力比µ与PGA的对应关系，得到100个相应的离散点，通过对数回归分析得到拟合结果.各构件在不同破坏状态下的需求能力比µ与地震加速度峰值PGA的关系可以表示为[9]

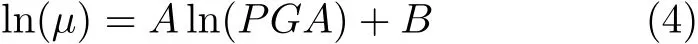
其中，µ为结构的需求能力比；A和B为回归系数，通过最小二乘法得到.

由式(1)和式(3)结合3.1节中损伤指标的定义，可以得到在不同损伤状态下桥墩、活动支座以及主梁梁端与桥台之间发生碰撞的超越概率及易损性曲线,分别如图4～图6所示.

从图4中可以看出：在多遇地震作用下(PGA= 0.11g时)，②号桥墩出现轻微破坏的概率是20%；出现中等破坏的概率是 6%；在罕遇地震作用下(PGA=0.51g时)，出现严重破坏的概率为68%，出现完全破坏的概率为25%.当破坏的超越概率为50%时，桥墩出现轻微破坏、中等破坏、严重破坏和完全破坏对应的PGA平均值分别为 0.13g,0.17g, 0.45g和 0.64g.分析表明：在多遇地震作用下桥墩会出现轻微破坏和中等破坏，而严重破坏与倒塌破坏只有在罕遇地震作用下才会发生，主要是由于桥墩能够承受较大的力，体现了桥梁构件的延性设计需求.

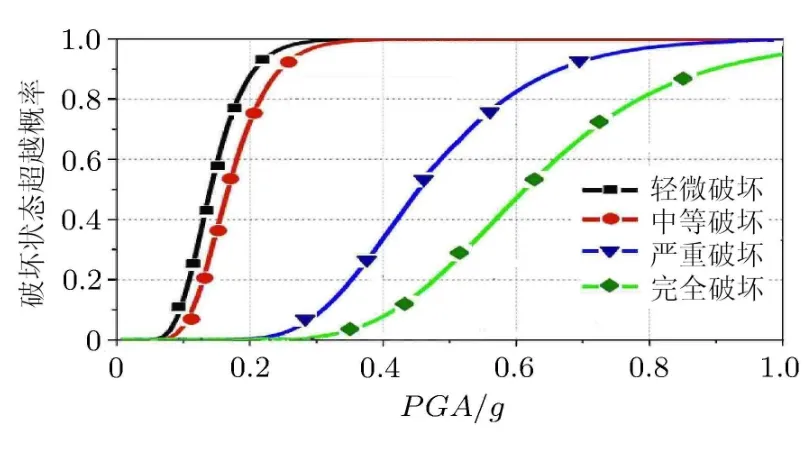
图4 ②号桥墩破坏的易损性曲线

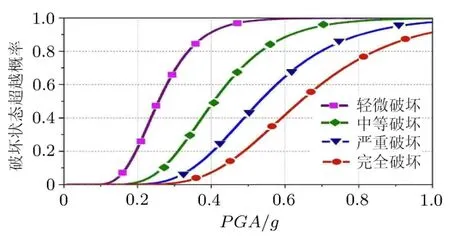
图5 支座的易损性曲线

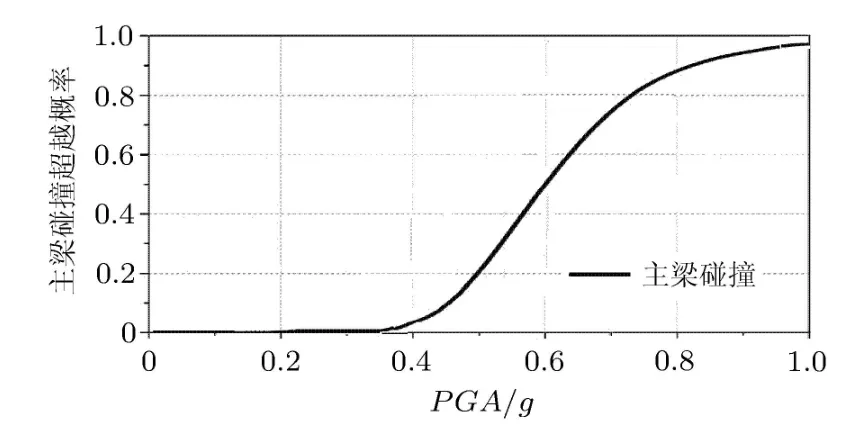
图6 主梁与桥台之间碰撞的易损性曲线

图5 中可以看出：在多遇地震作用下(PGA= 0.11g时)，支座不容易发生破坏，但是在罕遇地震作用下(PGA=0.51g时)，支座发生轻微破坏、中等破坏、严重破坏和完全破坏的概率分别为97%,75%, 41%,23%.从图 6可以看出：在多遇地震作用下(PGA=0.11g时)，主梁梁端与桥台不会发生碰撞现象；但是在罕遇地震作用下(PGA=0.51g时)，主梁梁端与桥台发生碰撞的概率为20%左右.

3.3 基于可靠性理论的桥梁整体结构系统易损性分析

对于桥梁整体结构失效概率的评价，需要考虑桥梁各个构件的易损性评价.可以利用1阶可靠度理论，估计各个损伤状态下结构的失效概率[6]

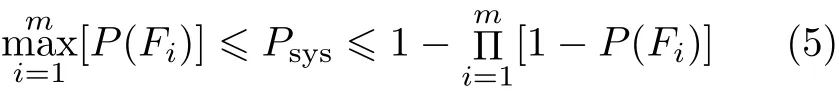
P(Fi)表示第i损伤状态下的失效概率(超越概率)；Psys为桥梁系统在各个损伤状态的失效概率 (超越概率)；m为桥梁系统构件数量.

由于一阶可靠度理论没有考虑结构不同损伤状态下的失效模式之间的联系.而对于多跨连续梁桥，3.2节中对桥梁各构件的易损性分析评价表明，桥梁整体结构的安全主要是由桥墩和支座控制的.因此，需要考虑两种主要破坏损伤状态下 (桥墩的破坏和支座失效)结构失效模式之间的相关性.本文采用2阶可靠度理论，考虑不同损伤状态下失效模式之间的联系，来估计各个损伤状态下结构的失效概率区间[6]

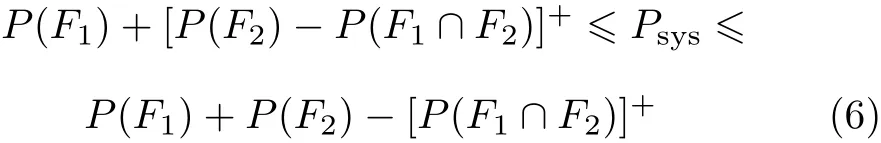
其中[]+=max(,0),P(F1∩F2)表示两种损伤状态下结构失效破坏模式同时发生的超越概率.由式(3)可以分别计算两种失效状态的概率，两种失效模式交集的概率可以通过对两元正态密度函数双重积分得到.进一步计算得到桥梁整体结构的失效概率(超越概率)[6]

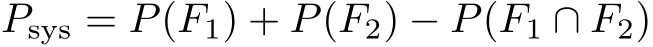
由式(5)和式(7)计算得到两种桥梁整体结构的失效易损性曲线，如图7所示.从图中可以看出：基于一阶可靠度理论得出的整体结构的易损性曲线，可以用来评价桥梁整体结构在地震作用下的失效概率区间范围，在罕遇地震作用(PGA=0.51g)下，桥梁整体结构的失效概率(超越概率)介于21%～30%范围之间，同时桥梁整体结构的失效概率的上界易损性曲线与活动支座失效的易损性曲线几乎是相重合的.基于二阶可靠度理论得出的整体结构的易损性曲线，在罕遇地震作用(PGA=0.51)下，桥梁整体结构的失效概率为21%.但是不管是基于一阶还是二阶可靠度理论进行易损性分析时，在多遇地震作用(PGA=0.11g)下，桥墩和支座都不会发生破坏或者失效，可能比较容易发生轻微破坏或者中等破坏；而在罕遇地震作用(PGA=0.51g)下，桥墩发生完全破坏和支座失效的超越概率分别是10%和22%.这表明结构要进行多重抗震设防.

图7 基于可靠理论的桥梁整体结构易损性曲线

4 结 论

本文同时考虑近场地震动随机性及结构参数随机性,对混凝土连续梁桥进行不同破坏状态下的增量动力分析.主要得到以下结论：

(1)考虑了桥墩、支座构件及主梁的碰撞损伤，分别得到了各构件(桥墩、支座、碰撞)的易损性曲线.分析表明：对于多跨连续梁桥，主梁梁端与桥台之间碰撞对于整体结构的破坏概率相对比较小，而桥墩破坏概率和活动支座的失效概率都比较大，更容易发生极限状态破坏.因此桥梁整体结构的安全主要是由桥墩和支座控制的.

(2)综合考虑桥墩破坏以及支座失效两种模式之间的相关性，根据可靠度理论得到了桥梁整体结构的易损性曲线.桥梁整体结构易损性曲线显示出桥梁结构要进行多重抗震设防.相对于一阶可靠度理论，采用二阶可靠度理论分析得出的桥梁整体结构的失效具有更小的概率区间，基于二阶可靠度理论的评价较为合理、更加安全可靠.

1 Jangid RS,Kelly JM.Base isolation for near-fault motions.Earthquake Engineering and Structural Dynamics,2001, 30(5)：691-707

2 Loh CH,Wan S,Liao WI.Ef f ects of hysteretic model on seismic demands：consideration of near-fault ground motions.The Structural Design of Tall Buildings,2002,11：155-169

3 赵风新,韦韬.近断层速度脉冲对钢筋混凝土框架结构地震反应的影响.工程力学,2005,25(10)：150-193

4 马宏伟,聂振华.桥梁安全监测最新研究进展与思考.力学与实践,2015,37(2)：161-170

5 李刚,程耿东.基于性能的结构抗震设计——理论、方法与应用.北京：科学出版社,2004

6 葛胜锦,熊治华,翟敏刚等.中小跨径混凝土连续梁桥地震易损性研究.公路交通科技，2013,30(7)：60-65

7 李立峰,黄佳梅,吴文朋等．基于IDA的高墩大跨桥梁抗震性能评估.地震工程与工程振动,2012,3(1)：68-77

8 吴巧云，朱宏平，樊剑.基于性能的钢筋混凝土框架结构地震易损性分析.工程力学,2012,19(9)：117-123

9 Barbieri N,Honorato de Souza O Jr,Barbieri R.Dynamic analysis of transmission line cables.Part I-linear theory.Mechanical Systems and Signal Processing,2004,18：659-669

10 姜维.连续桥梁的地震易损性分析.[硕士论文].武汉：华中科技大学,2012

11 Mander JB,Priestley MJN,Park R.Observed stress-strain behavior of conf i ned concrete.Journal of Structural Engineering,1988,114(8)：1827-1849

12 FEMA 356.Prestandard and commentary for seismic rehabilitation of buildings.Washington DC：American Society of Civil Engineers,2000

13 JTG/TB02-01-2008公路桥梁抗震设计细则.北京：中国建筑工业出版社,2008

(责任编辑：刘希国)

SEISMIC FRAGILITY OF THE RC CONTINUOUS GIRDER BRIDGE UNDER NEAR-FAULT GROUND MOTIONS1)

LIU Qiang2)WANG MiaofangYAN Tongmei
(College of Engineering Technology,Jimei University,Xiamen 361021,Fujian,China)

The seismic fragility of a RC(reinforced concrete)continuous girder bridge is analyzed,with consideration of damages of bridge piers,bearing components and the collision of the main beam.In view of the structural parameter randomness of the bridge structure,20 near-fault ground motions are selected from the PEER(Pacif i c Earthquake Engineering Research database),and a large number of random structure samples are established.Using the bridge damage index under dif f erent damage states,the fragility curves of the bridge components and the bridge system are obtained based on the structure of the capacity and the demand.According to the actual seismic demand of similar as-built bridges,the damage states can be obtained in the sense of probability,and provide a reference for future seismic damage predictions.

RC(reinforced concrete)continuous girder bridge,near-fault ground motions,seismic fragility analysis,damage index,pier

TU311.3

A

10.6052/1000-0879-16-205

2016-06-20收到第1稿，2016-10-31收到修改稿.

1)福建省自然科学基金(2016J01242)、福建教育厅自然科学基金(JA13188)和福建省大学生创新创业基金(201610390069)资助.

2)刘强，教授，博士，主要从事地震工程、工程抗震与减震控制研究.E-mail：liutanq007@aliyun.com

刘强,王妙芳,严通梅.近断层地震作用下钢筋混凝土连续梁桥地震易损性分析.力学与实践,2017,39(1)：40-44

Liu Qiang,Wang Miaofang,Yan Tongmei.Seismic fragility of the RC continuous girder bridge under near-fault ground motions.Mechanics in Engineering,2017,39(1)：40-44