载人登月转移轨道偏差传播分析与中途修正方法概述1)
李海阳 贺波勇 曹鹏飞
(国防科学技术大学航天科学与工程学院,长沙410073)
专题综述
载人登月转移轨道偏差传播分析与中途修正方法概述1)
李海阳2)贺波勇 曹鹏飞
(国防科学技术大学航天科学与工程学院,长沙410073)

李海阳,1972年生,力学学科教授,兼任载人航天工程轨道专家组专家、湖南省力学学会副理事长.长期从事载人航天系统分析与仿真领域科研工作.在计算结构力学、载人飞船逃逸与应急救生、交会对接轨道动力学与控制、“嫦娥工程”等方面开展了大量深入系统的基础研究,作为技术负责人组织开发了多个大型仿真系统,成功应用于载人航天工程等国家和军队重大任务.获军队科技进步一等奖2项、二等奖6项,2011年获“中国载人航天工程突出贡献奖”,发表科技论文100余篇,其中SCI数据库收录30篇,获批国家专利10项,软件著作权8项.
载人登月转移轨道是指地月转移轨道和月地返回轨道,其上飞行器飞行时间长、动力学模型复杂、非线性强且变系数.因此,工程任务中偏差不可避免,对偏差的控制直接影响任务执行的效果甚至成败.在概述载人登月转移轨道研究基础上,总结了偏差传播分析方法、最优中途修正策略及中途修正瞄准算法.最后,对我国未来载人登月转移轨道中途修正提出一些建议.
载人登月,转移轨道,偏差传播分析,中途修正
引言
20世纪50-60年代,美国和苏联为了争夺世界霸权,在航天领域展开了激烈的竞争.美国在1962年7月11日,确定了Apollo登月计划方案,并在1969年7月20日,用Apollo-11飞船将航天员送上了月球[1].苏联也在1964年8月3日提出了N1-L3载人登月计划,但由于N1火箭几次发射失败,该计划以失败告终[2].21世纪以来,世界范围内掀起了月球探测的第二轮热潮.以美国[3]、俄罗斯[4]、欧空局[5]、日本[6]、印度[7]为首的世界航天强国或组织,先后提出了自己未来20~40年的探月计划,不约而同地将载人登月作为探月的目标.2007年1月,中国科学院空间科学与应用研究中心学术委员会成功举行了“载人登月科学问题”专题学术讨论会,会议讨论了中国在载人登月问题上的基本思路和系统概念,为后来载人登月预先研究提供了积淀,各方机构正在积极有序地进行该方面预先研究工作[8].
目前提出或采用过的地月空间转移轨道大致可以分为4类:(1)大推力化学发动机直接快速转移, (2)利用地月系 L1点间接过渡方式,(3)利用日地系与地月系不变流形相交的弱稳定边界转移方法, (4)小推力转移方式[9].载人登月转移轨道指载人飞船往返于地月之间的轨道,与无人月球探测器转移轨道相比,载人登月转移轨道除满足天体力学、运动学自然规律、测控通讯等必要条件外,还必须考虑航天员生保能力及安全返回地球的任务中止能力.快速转移方案又可分为霍曼转移、双椭圆转移、自由返回轨道、混合轨道、Belbruno-Miller轨道、地月循环轨道转移方案、定向环调相转移等[10].
自20世纪60年代Apollo工程起,载人登月轨道优化设计成为月球及深空探测领域的热门问题,该问题可以归结为一类带有状态约束和控制约束的非线性最优控制问题.由于高精度动力学模型非线性强、星历求解系数和摄动项多等特点,出现了多种简化动力学模型和不同约束处理的求解方法,郑爱武等[11]对传统自由返回轨道、混合轨道及其约束处理、问题求解做了比较系统的论述.宝音贺西等[12]对载人登月多段自由返回轨道、地球和月球附近交会对接及全月面到达问题的研究做了现状分析和展望.陈海萍[13]、郗晓宁[14]对任务中止轨道问题做了详细的研究论述.
转移轨道优化问题是航天器轨迹优化理论和方法在载人登月具体任务中的应用[15].贺波勇[10]的研究表明,双二体假设圆锥曲线拼接模型和多圆锥截线模型是比较接近高精度动力学模型的简化动力学模型.其中,双二体假设动力学模型在实际优化问题中有多种适应性修改.黄文德[16]实现了该模型在传统转移轨道优化中的具体应用.Penzo[17]提出了多圆锥截线法,考虑地球非球形摄动影响及轨道预报校正,精度较双二体假设模型有所提高.彭祺擘等[18]和张磊等[19]分别提出了串行优化和多级迭代插值求解高精度动力学模型下转移轨道优化方法.
Kizner等[20]在Apollo工程时期指出,做好标称轨道设计同时,偏差传播分析与轨道修正控制工作对于飞行任务的各个阶段都是非常重要的.本文在概述了载人登月转移轨道研究现状基础上,重点概述了偏差传播分析方法、最优中途修正策略及中途修正瞄准算法.
1 偏差传播分析方法
1.1 Monte-Carlo打靶统计
载人登月转移轨道具有航天器飞行时间长、动力学模型复杂、非线性强且变系数的特点,是典型的非线性系统[21].非线性系统可以分为非本质非线性和本质非线性两类,前者能够用小偏差线性化方法进行线性化处理,后者不能用小偏差线性化方法处理,如混沌系统等.对于非线性系统本质不清楚的问题,通常使用Monte-Carlo打靶统计方法获得初步认识.在地月转移轨道问题中,何巍等[22]在研究低能耗地月转移轨道中途修正问题时,采用Monte-Carlo统计方法,仿真计算了各种误差情况下,低能耗地月转移轨道误差传播和中途修正终端误差精度.张磊等[23]在研究月地转移轨道中途修正问题中,采用 Monte-Carlo统计方法,计算统计了月地转移轨道偏差传播和再入参数及落点位置精度.贺波勇[10]参考“嫦娥一号”卫星地月转移轨道入轨偏差[24],设置入轨位置偏差3σr=5km,速度偏差3σv=5m/s,以一条地月自由返回轨道为例,Monte-Carlo打靶1000次统计结果显示:入轨点协方差传播至近月点的增益约为106,约有17%概率撞月,近月点如果不制动,返回地球再入点协方差的增益约为109.该工作定量描述了载人登月转移轨道非线性程度,间接证明了标称地月转移轨道在工程实用中需要中途修正的必要性.
1.2 无迹变换的协方差分析
基于无迹变换的协方差分析法 (unscented transform covariance analysis method,UTCAM),主要借鉴UKF(unscented Kalman f i lter)的均值和协方差更新思想.无迹变换是一种计算随机变量经过非线性变换后的统计特性方法,基于近似非线性函数的概率密度分布比近似其函数更容易这一事实,无迹变换的基本思想是用一组确定的离散采样点(σ点)来近似状态变量的分布,再让这些σ点随非线性系统变换,统计变换后的σ点集的统计信息[25].黄海兵[26]采用无迹变换分析了空间站调相偏差特性,并与商业软件STK的结果进行了对比验证,证明了该方法步骤明确,操作简单,计算快速等优点.文献[10]采用无迹变换方法分析了载人登月转移轨道偏差传播问题,结果与STK-HPOP-Covariance协方差分析模块计算结果吻合.
1.3 标称轨迹真线性化方法
线性系统具有叠加原理、Laplace变换、Fourier变换等成熟理论基础.研究非线性系统偏差传播时,首先想到的是真线性化协方差分析方法,对于非本质非线性系统,真线性化方法具有较强的工程实用性.Uesugi等[27]和孙宝忱等[28]研究表明,在精度要求不高的情况下,可以用地球中心引力场二体轨道解析方法计算偏差传播矩阵,结果与数值积分方法基本吻合.这是因为地月转移轨道实际上绝大部分未进入月球影响区,按照近地卫星摄动理论,将月球和太阳引力等其他作用力看成摄动力或者忽略,可以用解析方法得到一定精度的偏差协方差矩阵,这种方法仅适用于进入地月转移轨道不久的飞行器.贺波勇等[21]在研究载人登月转移轨道偏差传播机理时,基于文献[29-31]关于飞行器在地月空间受力分析结论,以标称地月转移轨道数据在每个积分点进行真线性化Taylor展开、连乘,求解偏差传播矩阵,分析了一条自由返回轨道地月转移段的摄动力角色变化及偏差二阶微分方程系数大小变化,揭示了转移轨道偏差传播机理,也解释了文献[28]中协方差分析方法仅近地段精度可信的原因.彭祺擘等[32]利用真线性化思想,研究了会合坐标系中地月转移自由返回轨道的偏差在绕月后急剧增益及平面内偏差椭圆变化特性.
2 最优中途修正策略
2.1 传统中途修正策略
地月转移轨道受到的摄动力复杂,且量级随飞船空间位置变化巨大.一次中途修正后的残差沿轨道传播相当长的时间仍有可能超出任务精度要求.如何确定最优修正次数和修正时刻以使燃料消耗尽可能少和终端偏差满足要求是20世纪60年代的热点研究问题.中途修正策略可以根据是否严格要求终端时间分为两大类:FTA(f i xed time of arrival)和VTA(variable time of arrival),FTA对终端时刻要求较高,对中途修正次数和能量消耗不追求最优,而VTA适合终端时刻不太严格的任务,要求修正次数尽可能少,能量消耗最优.比较典型的中途修正策略有方差比(variance ratio)策略,动态规划(dynamic programming)策略和间距比(spacing ratio)策略.随着智能进化算法的发展,国内学者将其用在航天器转移轨道中途修正策略中.
2.1.1 方差比策略
Battin[33]的方差比策略是一种次优中途修正策略,其基本思想是事先指定一定常比例,通过比较中途修正后估计方差和不确定性因素估计方差之比与该定常比例大小,产生中途修正策略.该策略需要工程人员结合具体转移轨道和先验知识给出这一定常缩小比例.
2.1.2 动态规划策略
Pfeiffer[34]的动态规划策略是一种使目标函数最小的策略确定方法,目标函数一般包括燃料消耗和终端状态偏差等.不同目标参数权值需要动态调整.郗晓宁等[35]以一条地月转移轨道为例,初制导以速度控制关机,总飞行时间为74小时,演示了动态规划策略在第一次中途制导和第二次中途制导时机确定中的应用.
2.1.3 间距比策略
Breakwell[36]的间距比策略的思想是尽快进行首次中途修正,以较小的燃料消耗代价大幅减小入轨偏差,以后各次修正时机的选择是按照修正效果与前一次修正效果的比值为常数这一条件确定的,直至满足误差要求,不再进行修正.间距比策略用数学语言描述为:尽快进行初次修正,然后选择修正时刻为t1,t2,…,tN,N为不定数,满足设定条件

式中,Δvn为施加速度增量的大小;E表示数学期望,Breakwell得出如下公式
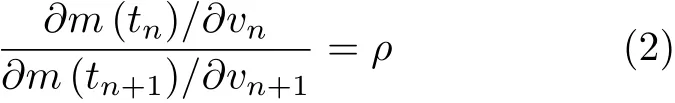
其中,ρ为某一常数;m为某一目标参数.间距比策略简单易行,得到了广泛应用[37-40].
2.2 进化算法求解策略
随着计算机硬件能力的跨越式发展,智能进化算法在工程决策和优化问题中发挥的作用日益增大.用智能进化算法求解中途修正策略问题的核心思想是将多目标多约束决策问题转化为多参数多目标优化问题,采用不同的算法步骤和多次迭代搜索计算,得到Pareto最优解集,再根据具体任务和一定技术经验选择一个修正策略.
卢山等[41]基于蚁群算法研究了转移轨道中途修正问题的最优修正时机.王蒙一等[42]研究了多目标进化算法在航天器转移轨道中途修正中的应用问题.张利宾等[43]研究了NSGA-II算法在火箭上面级中途修正问题中的应用.贺波勇[10]考虑地面测控弧段约束,采用NSGA-II算法求解了地月转移中途修正残差与终端误差两个优化目标Pareto前沿.
3 中途修正瞄准算法
地月转移轨道中途修正算法按照历史发展顺序,可以大致分为三类:一是20世纪大多数航天任务采用的基于二体轨道理论的摄动制导算法;二是基于显式制导思想的迭代算法,具有精度高,修正次数少等优点,也是目前工程中使用的方法;三是基于优化算法的瞄准算法,工程中未见成熟应用.
3.1 摄动制导瞄准算法
摄动制导瞄准算法是将轨道方程局部线性化,采用微分校正思想迭代收敛,算法步骤简单,收敛情况取决于线性化近似程度[44],常见于早期弹道导弹制导控制问题中[45].胡少春等[46]将摄动制导思想应用于日晕轨道中途修正问题.罗宗富等[47]将摄动思想应用于双月旁转向轨道中途修正问题.Kizner等[20,48]发现在目标星B平面参数与轨道状态量的偏差量之间存在比较好的线性关系,这大大提升了摄动制导算法在工程中的精度.谷立祥等[49]利用B平面设计地月转移轨道,本质是摄动制导迭代收敛.高飞等[50]应用B平面参数求解了火星转移轨道中途修正问题.
3.2 显式制导瞄准算法
显式制导算法一般通过二体轨道或其他比较简单的解析算法来与实际轨道比较,获取补偿速度,如此迭代多次,直到求解的中途修正脉冲满足要求即可.这种算法有很多种,在月球探测和火星探测任务中常用.20世纪 60年代以 Breakwell等[51],Stern等[52]学者的方法较典型,21世纪产生了精度和效率都大幅提升的算法,以Robert等[53],周文艳等[54]学者的方法较典型.郗晓宁等[35]在研究地月转移轨道中途修正时给出了一种以月球影响区为瞄准点的显式制导算法,简单易实现.胡军等[55-56]在我国探月工程月地返回轨道中途修正问题中实现了预报显式制导算法.
3.3 基于优化算法的瞄准方法
如果把中途修正速度脉冲当作优化参数,将轨道终端状态当作优化目标,中途修正瞄准问题可以归为非线性规划问题.用于地月转移轨道中途修正制导的优化算法可以分为两类:一类是智能进化算法,一类是局部收敛算法.
3.3.1 智能进化算法
智能进化算法是模拟自然界生物、物理、数学等现象,以随机搜索和大概率统计收敛原理达到全局收敛的成效,不依赖初值,效率较低.因具体问题不同出现了名目繁多、各种因地制宜的改进、改良和结合版本[10].谷立祥等[49]使用遗传算法和B平面参数求解地月转移轨道中途修正问题,卢山等[57]基于自适应模拟退火算法求解转移轨道.
3.3.2 局部收敛算法
局部收敛算法是一门古老的学科,基本的进退法、黄金分割法、Newton梯度法等,需要初值,收敛解为局部最优解.目前比较流行的算法有序列二次规划算法、内点罚函数法、信赖域反馈等,贺波勇等[58]比较了这3种方法在求解月地返回轨道中途修正时的优劣,得出内点罚函数法具有一定优势的结论,原因是该算法采用黄金分割法,不需要计算梯度信息等参数,并结合某工程任务开发了相关软件[10].
4 结论与建议
载人登月工程是一项技术含量高、复杂度大的大科学工程,具有极高的风险性,而中途修正直接关系到任务执行精度.本文概述了国内外载人登月转移轨道研究方法及相关的研究成果,总结了转移轨道偏差传播分析方法、最优中途修正策略及中途修正瞄准算法等研究工作现状.总的来说,目前对于载人登月转移轨道中途修正问题的研究考虑的工程实际约束还比较简单,一味地追求速度增量最优(燃料最少)并不贴合实际需求.从实际计算结果来看[10,59],载人登月中途修正瞄准速度增量(燃料消耗)与初始偏差、测量偏差、执行偏差等工程实际情况有关,但在测控区间内变化不大,一般在几米每秒至十几米每秒量级变化.建议:
(1)对载人登月工程轨道偏差进行具体分析、对工程约束进行充分论证,以便确定合理的中途修正策略和预留速度增量;
(2)对偏差修正和故障预案进行一体化设计,确定两者的边界和判断准则;
(3)通过地面测控中心提高修正瞄准指令精度,减少中途修正次数.最优时机要综合考虑任务窗口,测控约束和航天员生物钟等因素,在预留速度增量容许情况下,将修正轨控时机避开航天员休息时段.
1 水天.永远的辉煌 ——“阿波罗”登月回顾.中国国家天文,2008,12:92-97
2 哈维.苏联/俄罗斯探月历程.邓宁丰译.北京:中国宇航出版社,2009
3 President Bush GW.The vision for space exploration. 2004.http://history.nasa.gov/vision_for_space_exploration. pdf
4 魏雯.2006-2030年俄罗斯载人航天发展构想.中国航天,2007, 9:30-36
5 韩鸿硕,蒋宇平.各国登月计划及载人登月的目的与可行性简析.中国航天,2008,9:30-33
6 尚小桦,何继伟.日本 JAXA-2025规划及其航天发展的新动向.中国航天,2006,3:24-28
7 管春磊,周鹏,强静.国外载人登月发展趋势研究.国际太空, 2009,4:22-28
8 王赤,孙丽琳.展望中国人的登月梦想:“载人登月科学问题”专题学术讨论会成功举行.科学通报,2007,3:739-740
9 彭祺擘.考虑应急返回能力的载人登月轨道优化设计及特性分析.[博士论文].长沙:国防科学技术大学研究生院,2012
10 贺波勇.载人登月转移轨道偏差传播分析与中途修正方法研究. [博士论文].长沙:国防科学技术大学研究生院,2013
11 郑爱武,周建平.载人登月轨道设计方法及其约束条件概述.载人航天,2012,18(1):48-54
12 宝音贺西,李京阳.载人登月轨道研究综述.力学与实践,2015, 37(6):665-673
13 陈海萍.载人登月任务中止轨道特性分析.[博士论文].长沙:国防科学技术大学研究生院,2009
14 郗晓宁.载人登月任务中止轨道问题综述.中国科学技术科学, 2011,41(5):537-544
15 唐国金,罗亚中,雍恩米.航天器轨迹优化理论、方法及应用.北京:科学出版社,2012
16 黄文德.载人登月中止轨道的特性分析与优化设计.[博士论文].长沙:国防科学技术大学研究生院,2011
17 Penzo PA.Computing earth orbitness eff ects on lunar and interplanetary trajectory.AIAA 70-0097,1970
18 彭祺擘,沈红新,李海阳.载人登月自由返回轨道设计及特性分析.中国科学技术科学,2012,42(3):333-341
19 张磊,谢剑峰,唐歌实.绕月自由返回飞行任务的轨道设计方法.宇航学报,2014,35(12):1388-1395
20 Kizner W.A method of describing miss distance for lunar and interplanetary trajectories.Planetary and Space Science,1961,7:125-131
21 贺波勇,李海阳,张波.载人登月转移轨道偏差传播机理分析与稳健性设计.物理学报,2013,62(19):190505-1-8
22 何巍,徐世杰.地-月低能耗转移轨道中途修正问题研究.航天控制,2007,25(5):22-27
23 张磊,于登云,张熇.月地转移轨道中途修正方法及策略.航天器工程,2012,21(3):18-22
24 杨维廉,周文艳.嫦娥一号卫星地月转移轨道中途修正分析.空间控制技术与应用,2008,34(6):3-7
25 潘泉,杨峰,叶亮等.一类非线性滤波器——UKF综述.控制与决策,2005,20(5):481-489
26 黄海兵.空间站交会对接的若干动力学与控制问题.[博士论文].长沙:国防科学技术大学研究生院,2012
27 Uesugi KK,Ishiii JN.Geotail lauch window expansion and trajectory correction strategies:analysis and flight results. The 5th International Space Conference of Pacif i c-Basin Societies,Shanghai,1993
28 孙宝忱,荣思远.向月飞行轨道误差分析.导弹与航天运载技术, 2006,286(6):1-4
29 刘良栋,李果,潘科炎等.航天器轨道动力学与控制.北京:中国宇航出版社,2001
30 周文艳,杨维廉.月球探测器转移轨道的中途修正.宇航学报, 2004,25(1):89-92
31 郑爱武,周建平.直接再入大气的月地返回窗口搜索策略.航空学报,2014,35(8):2243-2250
32 彭祺擘,贺波勇,张海联.地月转移自由返回轨道偏差传播分析.深空探测学报,2016,3(1):56-60
33 Battin RH.Astronautical Guidance.New York:Mc Graw-Hill Book Company,1964
34 Pfeif f er CG.A dynamic analysis of multiple guidance correction of a trajectory.AIAA Journal,1965,3(9):1674-1681
35 郗晓宁,曾国强,任萱等.月球探测器轨道设计.中国北京:国防工业出版社,2001
36 Breakwell JV.Fuel requirements for crude interplanetary guidance.Advance in Astronautical Science,1960,5:53-65
37 Esposito BP,Bollman GW,Cangahuala AL.Navigating mars observer:lauch through encounter and response to space craft’s pre-encounter anomaly.AAS/AIAA Space Flight Mechanics Meeting,Pasadena,1993
38 Thurman SW,Vincenti MP.Guidance and navigation for the mars pethf i nd mission.Acta Astronautica,1995,35:545-554
39 Kawaguchi J,Matsuo H.Low-thrust f l yby guidance and an extended optimal spacing rule.Journal of Guidance, Control and Dynamics,1996,19(2):347-354
40 倪彦硕,施伟璜,杨洪伟等.利用Breakwell间距比法制定行星际探测中途修真策略.深空探测学报,2016,3(1):83-89
41 卢山,段佳佳,徐世杰.基于蚁群算法的转移轨道中途修正问题研究.系统仿真学报,2009,21(14):4400-4404
42 王蒙一,江涌.多目标进化算法在航天器转移轨道中途修正中的应用.航天控制,2009,27(5):52-57
43 张利宾,史晓宁,崔乃刚.基于NSGA-II算法的上面级转移轨道中途修正时机优化.控制与决策,2011,26(9):1382-1385
44 田野,张洪波,吴杰.基于轨道方程线性化的中段飞行轨道修正方法.飞行力学,2011,29(3);68-71
45 程国采.弹道导弹制导方法与最优控制.长沙:国防科技大学出版社,1987
46 胡少春,孙承启,刘一武.日晕轨道卫星的转移轨道中途修正研究.空间控制技术与应用,2012,38(5):21-26
47 罗宗富,孟云鹤,汤国建.双月旁转向轨道的修正方法研究.力学学报,2011,43(2):408-416
48 Kizner W.Some orbital elements useful in space trajectory calculations.Technical Report No.AD0263968,Jet Propulsion Labortory,1960
49谷立祥,刘竹生.使用遗传算法和 B平面参数进行月球探测器地月转移轨道设计.导弹与航天运载技术,2003,263(3):1-5
50高飞,苏宪程. 火星探测转移轨道中途修正分析.宇航学报, 2010,31(11):2530-2535
51Breakwell JV,Lars FH,Martin AK.Guidance phenomena for a mars mission.AAS Symposium on Exploration of Mars,Denver,1963
52Stern RG,Potter JE.Optimization of mid-course velocity corrections//Aseltine JA ed.Peaceful Uses of Autoination in Outspace.New York:Springer,1966
53Robert HB,Dennis V,Byrnes DJ,et al.Earth-mars transportation opportunities:promising options for interplanetary transportation.Battin Astrodynamics Conference, San Diego,CA,2000
54周文艳,杨维廉.月球探测器转移轨道的中途修正.宇航学报, 2004,25(1):89-92
55胡军,周亮.基于显式制导的月地返回轨道中途修正研究.中国空间科学技术,2013,5:7-14
56周亮,胡军.基于分段瞄准点预报显式制导的月地返回轨道中途修正研究.空间控制技术与应用,2013,39(4):1-6
57卢山,陈统,徐世杰.基于自适应模拟退火遗传算法的最优Lambert转移.北京航空航天大学学报,2007,33(10):1197-1195
58贺波勇,彭祺擘,李海阳.基于优化算法的月地返回轨道中途制导方法.中国宇航学会深空探测技术专业委员会第九届学术年会,杭州,2012
59Berry RL.Launch window and trans-lunar,lunar orbit, and trans-earth trajectory planning and control for the Apollo-11 lunar landing mission.AIAA 8th Aerospace Sciences Meeting,New York,1970
(责任编辑:胡 漫)
TRANSFER ORBIT DEVIATION PROPAGATION ANALYSIS AND MID-COURSE CORRECTION FOR HUMAN LUNAR MISSION1)
LI Haiyang2)HE Boyong CAO Pengfei
(College of Aerospace Science and Engineering,National University of Defense Technology,Changsha 410073,China)
The transfer orbit for the human lunar mission means that between the trans-lunar orbit and the trans-earth orbit,and it has the characteristics of long f l ight time,complex dynamics model,and strong nonlinear and variable coefficients.The controllability of the inevitable deviation af f ects the result of the task execution,even the success or the failure of the engineering task directly.This paper reviews the studies of the transfer orbit of human lunar mission,the analysis method of the deviation propagation,the mid-course correction optimal strategy and the mid-course correction aiming algorithm.At last,some suggestions are madefor the mid-course correction of the Chinese human lunar mission in the future.
human lunar mission,transfer orbit,deviation propagation analysis,mid-course correction
V412.4
A
10.6052/1000-0879-16-291
2016-09-07收到第1稿,2016-11-15收到修改稿.
1)国家自然科学基金(11372345,11402295)和国家重点基础研究发展计划(2013CB733100)资助项目.
2)李海阳,教授,博士生导师,研究方向为载人航天任务分析与仿真.E-mail:lihaiyang@nudt.edu.cn
李海阳,贺波勇,曹鹏飞.载人登月转移轨道偏差传播分析与中途修正方法概述.力学与实践,2017,39(1):1-6
Li Haiyang,He Boyong,Cao Pengfei.Transfer orbit deviation propagation analysis and mid-course correction for human lunar mission.Mechanics in Engineering,2017,39(1):1-6

