木材I/II复合型断裂破坏研究进展1)

赵艳华 李 征 常建梅†

∗(大连理工大学,海岸和近海工程国家重点实验室，辽宁大连116024)†(内蒙古大学交通学院，呼和浩特010070)

木材I/II复合型断裂破坏研究进展1)

赵艳华∗,2)李 征∗常建梅∗,†

∗(大连理工大学,海岸和近海工程国家重点实验室，辽宁大连116024)†(内蒙古大学交通学院，呼和浩特010070)

复合型应力状态是木材断裂破坏的主要受力模式，本文从复合断裂模型和试验方法两个方面回顾了木材复合断裂研究的发展历程.在介绍了木材复合断裂的经验模型和物理模型后，通过一组试验数据进行了这些断裂模型的比较，总结了各自的特点.同时，总结了确定这些模型而进行的各类试验方法，主要是I/II复合断裂模式，即断裂模式I和断裂模式II均存在的情况.最后阐述了木材复合断裂研究中的一些问题,并对今后的研究方向提出了建议.

木材,断裂力学,复合型断裂,应力强度因子,能量释放率

引言

木材是最为古老的结构材料，其历史可以追溯到金字塔时代.目前混凝土是建筑业中的主流材料，但随着公众对生态环境的日渐关注，可再生建筑材料将是日后建筑材料的发展趋势.在这种大环境下，木材凭借其易获性、质轻强高、良好的耐久性和工作性、在生长加工和使用上的简便性以及吸能、隔热、隔电的优点，在现代结构中得到了广泛的应用，不仅可用于商店、办公楼和住宅楼等民用建筑，在大跨桥梁和体育馆屋顶上也可见到木材的身影.木材的广泛使用与人类认识木材性能的过程紧密相关.传统的木结构设计基于材料的强度准则[1-3]，结果偏于保守.考虑到木材容易沿着纤维方向断裂，研究人员尝试将断裂力学应用于木材.1964年Porter首先利用能量平衡原理确定了美国白松的断裂参数[4]，开启了木材的断裂力学研究.其后各国研究人员进行了木材的基本断裂模式研究，即张开I型和滑移II型，而且研究成果主要集中在断裂韧度的确定方面.实际结构中的木材一般处于复合断裂模式，即基本断裂模式 I型、II型和 III型的不同组合，其中以 I/II复合型最为常见.木材的复合型断裂研究进展缓慢，研究成果相对有限，其原因与木材的内部结构密切相关.在微观层次上木材胞壁可视为纤维增强复合材料：晶胞纤维构成增强相，半纤维素和木质素为基体.从细观层次上看，木材是细胞结构，由截面为六边形的棱柱体细胞壁和气孔组成.而微观组成纤维的分布决定了平行于纤维方向的材料强度大于垂直于纤维方向的强度.在宏观层次上木材可视为树皮、边材和心材组成的复合材料.由于木材在生长过程中形成同心年轮，木材的力学性能呈现出近似的轴对称性.如果试件切割位置远离髓心，可忽略年轮的曲率影响.当坐标轴分别取为纤维方向L，径向R和切向T时，可将木材视为正交各向异性材料.

线弹性断裂力学范围内的经典复合断裂准则，如最大周向应力(maximum tangential stress,MTS)准则[5]、最大能量释放率(GE)准则[6]和最小应变能(S)准则[7],在运用于各向同性材料时取得了很大的成功，即能准确地预测开裂角度和开裂条件，但在应用于木材时却遇到了障碍.举例来说，对于II型加载条件，根据MTS准则得到的开裂角度与初始裂纹的夹角为-70.5°，可在木材试验中，开裂总是沿着纤维方向，与初始裂纹的方向无关.因此木材复合型断裂研究的一个主要内容就是建立适用的断裂准则.另一研究重点就是寻求可靠方便的几何形式，原因仍是木材的各向异性特征.因为裂纹尖端的断裂参数不仅与试件尺寸和施加的外载荷相关，还与材料的各个方向的弹性性能相关.用于木材复合型断裂研究的几何试件应使裂纹尖端的断裂参数易于确定.另外，试件的断裂还应能较方便地实现从I型经过复合型再到II型的完整过渡.木材复合型断裂的研究历史就是围绕这两个方面开展的，下面逐一介绍.

1 木材复合型断裂准则

对于正交各向异性的木材而言，其中裂纹的扩展可出现如图1所示的8类方式[8]，每类用一对字母表示，其中第一个字母表示裂纹面的法向，第二个字母表示裂纹扩展方向.由于年轮包含的密度梯度影响，径向裂纹扩展可能向着髓心也可能背离髓心，为区别起见，用“+”表示远离髓心，而“-”表示靠近髓心.

图1 木材的弹性主轴及裂纹扩展模式

与各向同性材料不同，在复合型加载条件下木材裂缝的扩展方向为纤维方向，因此木材复合型断裂不需要解决裂缝扩展方向问题，只需要建立断裂发生的条件即可.断裂准则的建立主要分两种渠道：一种是由试验结果拟合得到，一种是建立物理模型.这两类渠道得到的断裂准则可用统一的公式表示

其中，KI和KII分别为裂纹尖端I型和II型对应的应力强度因子.

1.1 试验拟合准则

在木材复合型断裂研究的早期阶段，主要采用数据拟合的经验公式.Wu[9]在1967年利用巴沙木I/II复合型试验(RL或TL)给出了以下经验公式

其中，KIc和KIIc为断裂I型和II型的断裂韧度.由于裂纹方向与弹性主轴方向L一致，而且采用了较大尺寸的板，因此KI和KII可以按照各向同性材料的无限大板应力强度因子公式计算.

Leicester[10]在 1974年根据松树的试验结果给出了比较保守的断裂准则

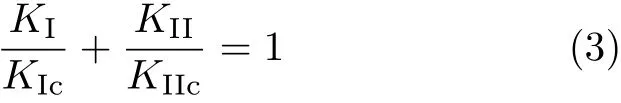
Williams等[11]在1976年通过楝树和欧洲赤松单边裂纹的TL模式试验，认为II型断裂对复合型断裂没有影响，即复合型断裂准则为

由于试验中KII/KI的比例最大约为3.5，因此式(4)有一定的局限性，不具有普遍型.

Hunt等[12]在1982年对波罗的海红木RL模式的复合断裂数据采用最小二乘法处理给出了复合断裂准则

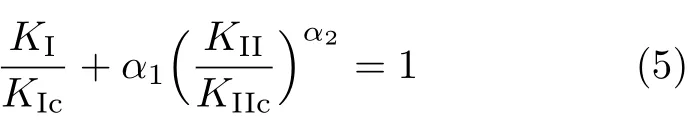
其中，α1和α2为拟合常数，与树种和裂纹方向相关.

Mall等[13]在1983年对东方红杉进行了TL模式的复合断裂试验，裂纹与外加载荷有一角度构成了I/II复合型断裂方式，裂纹尖端的KI和KII由有限元计算得到的节点位移根据文献[14]的方法得到.结果发现试验数据用式(2)可以很好地拟合.

1.2 物理模型准则

从20世纪80年代后期开始，木材复合型断裂研究不再单纯地依靠试验进行数据拟合，而是从理论上建立物理模型.Buczek等[15]在1985年用正应力比准则预测了各向异性材料的裂纹扩展角度.此模型认为在离裂纹尖端距离为r0的平面Φ上正应力为σΦΦ，平面Φ上的抗拉强度为TΦΦ，则裂纹扩展所在的平面为比值R(r0,Φ)最大的平面，其中

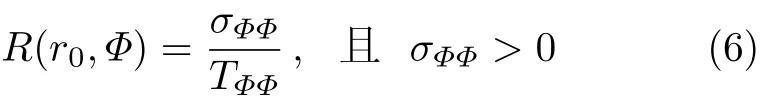
TΦΦ为裂纹可能扩展方向与纤维方向夹角β的椭圆函数，即

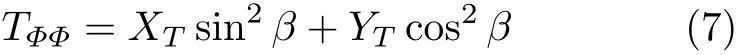
其中，XT为裂纹方向与纤维方向一致时的材料抗拉强度，而YT为裂纹方向与纤维方向垂直时对应的材料抗拉强度.

与最小应变能密度准则的比较证实正应力比准则可以用于各向同性材料裂纹的扩展角度预测.对于各向同性材料，TΦΦ=XT=YT为材料的抗拉强度，式(6)表达的复合型断裂准则退化为最大周向应力准则，即MTS准则[5].对于各向异性材料，正应力比准则再次证实了裂纹将沿着纤维方向扩展.但如果忽略TΦΦ的各向异性，还按照MTS准则预测，则裂纹扩展角度偏离原来裂纹平面50°，与试验结果不符.因此TΦΦ的加入可认为是各向异性特征对MTS准则的修正.

木材复合型裂纹断裂准则与裂纹尖端的应力场紧密相关，因此这里列出正交各向异性材料裂纹尖端的应力解，用于以下分析.如图2所示

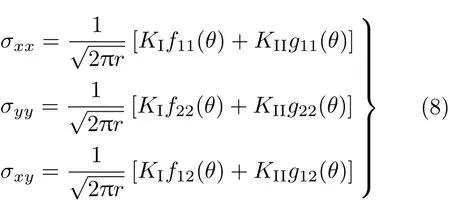
其中，无量纲参数fij和gij(i,j=1,2)与材料弹性常数相关，具体可参考文献[16].

和应力相对应的应变为

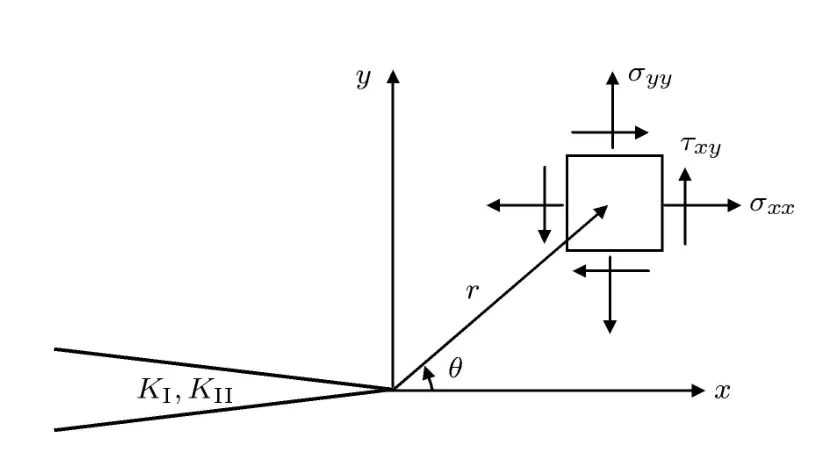
图2 裂纹尖端应力分布

其中，Ckl即为平面应力状态下的柔度系数；对于平面应变，其柔度为

如果将传统的最大能量释放率准则 (GE准则)[6]和最小应变能密度准则(S准则)[7]用于木材，在假定裂纹扩展方向即为纤维方向的基础上，木材复合型断裂准则分别为

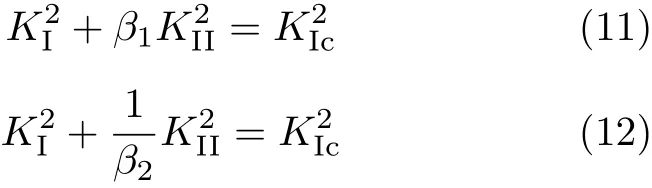
其中，材料常数β1和β2为

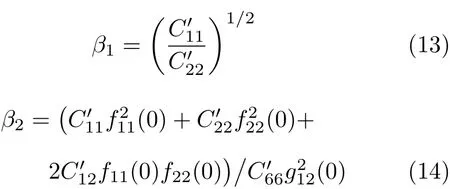
考虑到在纤维方向上，当只有KII存在时，周向应力为0.因此最大周向应力准则MTS不适合各向异性材料.Jernkvist基于平面内最大主应力建立木材复合型断裂准则[16-17]，即离裂纹一定距离的最大主应力达到临界值.在纤维方向上主应力有局部最大值，因此可合理假定裂纹扩展方向为纤维方向，而不是最大主应力方向.

根据裂缝尖端前沿的最大主应力可得复合型裂纹扩展条件为

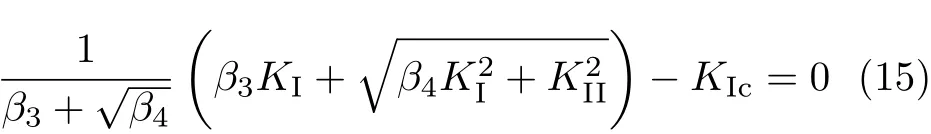
其中

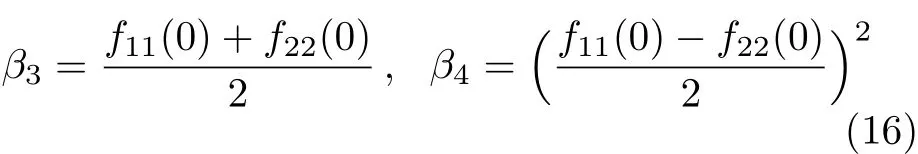
文献[16]同时采用最大能量释放率准则和最小应变能密度准则与最大主应力准则进行了比较，试验数据采用波罗的海红木的RL模式[12]和东方红杉的TL模式[13]，结论是GE准则和S准则过于保守.但与东方红杉的TL模式试验数据比，最大主应力准则也有些保守.

式(15)和式(16)不仅适用于裂纹方向平行于纤维L方向的情况，也适用于裂纹方向垂直于L方向的情况，即LT或LR.只不过对于后者，由于裂纹扩展仍沿着L方向，在垂直于初始裂纹的方向上将出现分支裂纹(如图3所示)，因此式(15)中的KI和KII应采用分支裂纹尖端的应力强度因子代替，即

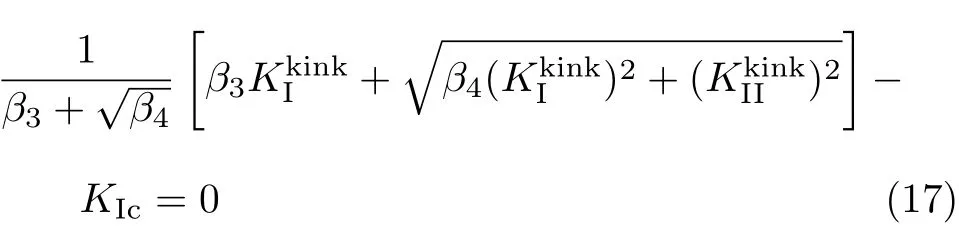
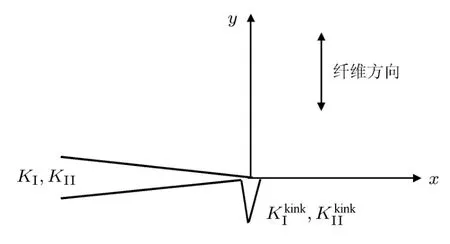
图3 垂直于纤维方向裂纹的扩展

当分支裂纹长度远小于试件平面内尺寸时，分支裂纹尖端的应力强度因子与主裂纹尖端的应力强度因子KI和KII的关系为

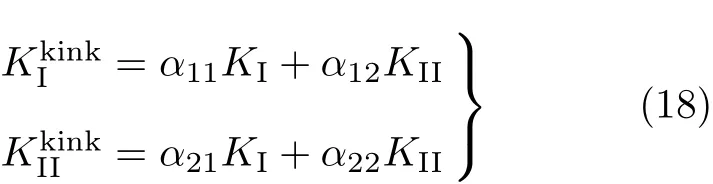
其中，αij(i,j=1,2)是木材材料的弹性常数.对于各向同性材料而言，分支裂纹裂尖的应力强度因子是主裂纹尖端应力强度因子和分支裂纹与主裂纹夹角的函数.

根据对试验结果的观察和分析，Jernkvist用一个概念模型定性解释了木材I型和I/II复合型裂纹扩展的不同(如图4).其中，I型裂纹是沿着管胞壁进行，所需能量较小，而I/II复合型裂纹由于尖端最大主应力的方向不一定是沿着纤维方向，因此I/II复合型裂纹扩展不仅包括管胞壁的分离，还有众多微裂纹跨过胞壁进行汇聚的过程，所需的能量比纯I型大，而且断裂面也不如纯I型光滑.

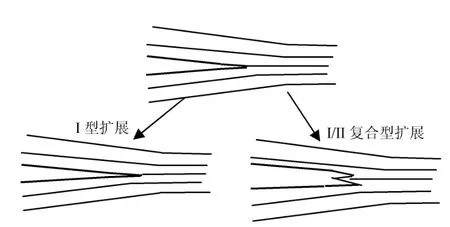
图4 纤维方向裂纹扩展的概念模型

Jernkvist在进行试验研究其最大主应力准则时，发现LR模式的挪威松双悬臂梁结果偏于保守，Jernkvist将其归结为裂纹尖端的T应力影响.T应力是裂纹尖端平行于裂纹方向的应力分量，是一个常量.线弹性断裂力学由于只考虑应力强度因子所在的奇异项，一般忽略T应力.但当T应力相比应力强度因子大于某一程度后，T应力将对裂纹扩展方向和条件产生明显的影响，尤其是对于II型裂纹扩展[18-20].而T应力对各向异性材料断裂的影响却鲜有涉及.Jernkvist是较早考虑T应力对木材断裂影响的研究人员.

断裂力学中一般将裂纹处理为理想的数学裂纹，即没有厚度.荷兰学者Put认为这样处理不能正确反映裂纹特性，建议将裂纹处理为扁平椭圆.另外，木材可视为纤维增强基体的复合材料，对于各向同性的基体而言，Put[21]采用了应力型复合断裂模型

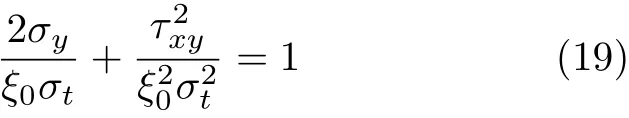
其中，σy和τxy分别为作用在椭圆裂纹的应力边界条件，σt为切向应力临界值.而ξ0为椭圆坐标系下裂纹边界几何条件.有趣的现象是式(19)恰好为Wu提出的经验式(2)提供了理论支持.

值得注意的是式(19)是针对各向同性的基体材料，若将其转化为正交异性应力，则需通过Airy应力函数进行，式(19)变为

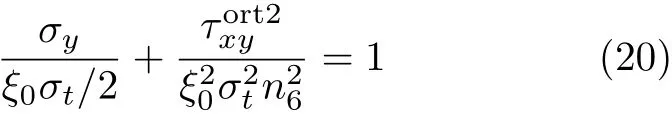
其中，n6为材料系数，与各项异性材料的柔度相关，见文献[21].

2008年,Romanowicz等[22]结合非局部应力准则和微裂纹损伤模型用于木材，建立了木材复合型断裂准则.以RL模式为例，非局部应力断裂准则为

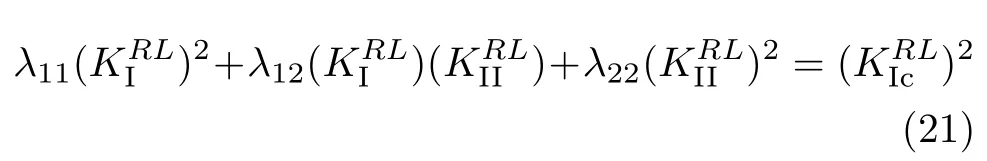
其中，λ11,λ12和λ22是裂纹预制方向与L方向夹角的三角函数，具体表达式见文献[22].对于裂纹方向本身就是L方向，则式(21)简化为

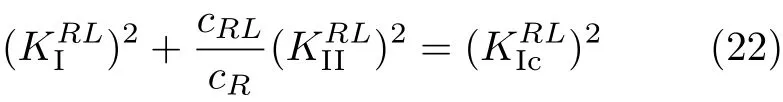
其中，cRL和cR分别表示起裂平面上滑移和张开方向的柔度，根据微裂纹密度和实际尺寸计算[23].亦可假定开裂必通过KIRcL和KIRIcL点，因此

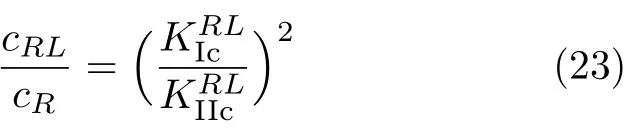
非局部应力断裂准则与先前的木材复合型断裂准则相比，一个进步就是考虑了裂纹初始方向与L方向成一角度时的复合断裂问题.而且文献[17]试验结果再次证实了GE准则和S准则的保守性，以及最大主应力准则对断裂韧度的高估性.但是非局部应力断裂准则需要II型断裂韧度，这个参数的试验结果带有很大的不确定性，与试验方法，试件几何形式以及T应力效应都有很大的关系[18-21].

2010年,Gowhari-Anaraki等[24-25]认为先前建立的大部分木材复合断裂模型在以下3个方面存在缺陷：

(1)没有考虑断裂过程区的能量消耗；

(2)没有考虑裂纹方向与纤维方向不同的情况；

(3)没有考虑裂纹尖端T应力的影响.

在最大能量释放率基础上同时考虑以上因素，Gowhari-Anaraki等提出以下木材复合型断裂准则

式(24)与最大能量释放率GE准则式(11)形式一样，但考虑到断裂过程区能量损耗，ρ应采用损伤区的柔度，即

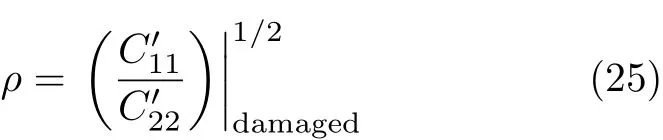
Gowhari-Anaraki等[26]建立了损伤区的解析模型，给出了ρ的解析公式

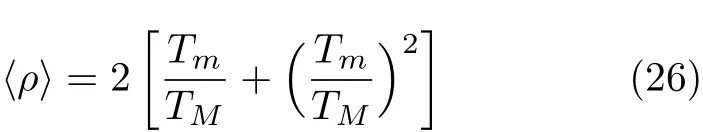
其中，三角括号代表平均值，因为ρ与坐标轴与木材纤维L方向的夹角有关；TM和Tm分别为平行和垂直纤维方向的强度，与式(7)中的XT和YT含义一致.

对于初始裂纹方向不再沿着纤维方向L时，断裂准则形式仍为式(24)，但是应力强度因子应采用分支裂纹，因为裂纹扩展方向总是纤维方向

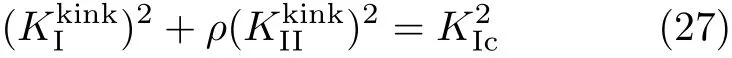
其中，分支裂纹尖端的应力强度因子KIkink和KIkIink按式(28)计算

式中，αij(i,j=1,2)是木材材料的弹性常数，与式(18)相同；bi(i=1,2)是材料柔度系数的函数；akink为分支裂纹长度；而T则为平行于裂纹尖端的应力常数.实际上早在1965年Sih确定各向异性材料裂纹尖端的应力场时就含有此常数项，文献[27]指出其值与几何形式和加载方式相关.

Gowhari-Anaraki等提出的这个模型认为作为平行于裂纹方向的应力，T应力对裂纹方向平行于L方向的复合裂纹开裂和扩展没有影响，但对初始裂纹与L纤维方向有夹角的情况则应考虑.

在2013年Fakoor等[28]考虑到各向同性材料最大剪应力破坏面，提出了木材复合型断裂的最大剪应力准则，即裂纹扩展方向由相对剪应力大小达到最大值确定，而裂纹扩展条件为此方向上的剪应力达到临界值.相对剪应力根据式(29)确定

其中，τ(r0,Φ)为距裂纹尖端距离为r0扩展面方向为Φ处的剪应力，T(Φ)为此扩展面的强度大小，根据式(7)确定[29].根据最大剪应力假定，木材复合型断裂发生条件为

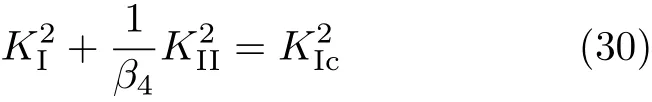
其中，β4系数的定义与式(16)相同.对于初始裂纹方向与L不一致的情况，采用支裂纹模型计算裂纹尖端的应力强度因子，计算同式(18).

本文选取文献[17]挪威松RL模式的断裂试验数据进行了各个模型的比较，见图5所示.

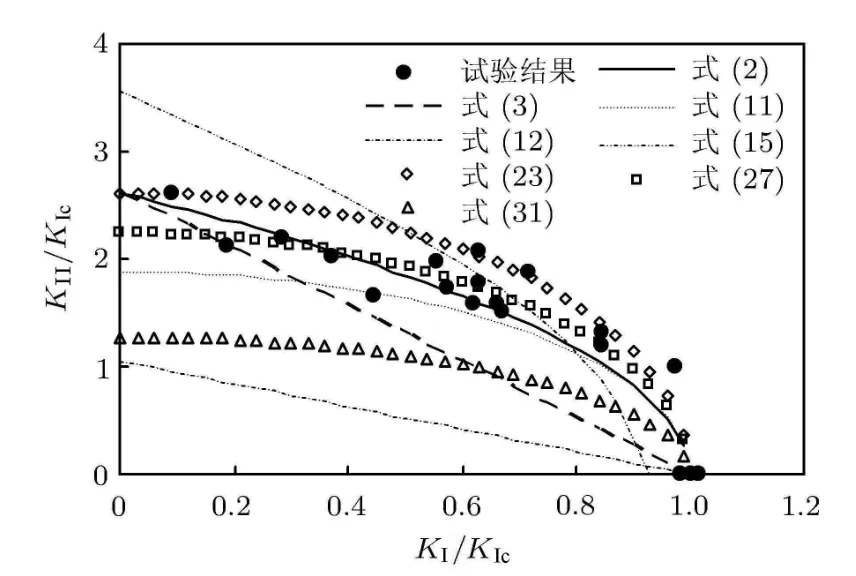
图5 各类模型与试验结果的比较[17]

通过对挪威云杉试验数据[17]的比较，发现经验公式中的线性关系式(3)、最大能量释放率准则式(11)、应变能密度因子准则式(12)以及最大剪应力准则式 (31)比较保守；而最大主应力准则式 (15)则高估了试验数据；Wu[9]提出的抛物线经验公式(2)、非局部应力准则式 (23)以及考虑损伤区的式(27)与试验数据吻合得较好.当然，以上结论都是在与文献[17]提供的试验数据进行比较后得出，不代表对其他试验也具有相同的结论.

以上介绍的木材采用的复合型断裂准则基本以应力强度因子作为断裂参数，其计算大部分采用有限元方法.对某些特殊的几何试件，可以通过简单的梁理论得到能量释放率G的解析表达式，而无需进行复杂的有限元计算.de Moura等[30]采用能量释放率G作为断裂参数，则其断裂准则可采用

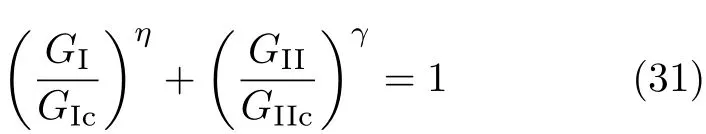
其中，GIc和GIIc分别为I型、II型裂纹对应的临界能量释放率，也称为断裂韧度；GI和GII分别为I/II复合型裂纹中 I型和 II型分量对应的能量释放率.对于线性关系，η=γ=1；对于二次关系，η=γ=2.

能量释放率G型断裂准则还可采用[31]

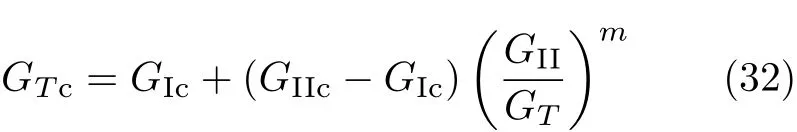
其中，GT为I/II复合型裂纹对应的总能量释放率，GTc为GT的临界值,m为半经验指数.

通过对葡萄牙海滨松RL模式的复合断裂试验，线性关系能较好地解释试验结果.

以上的能量释放率G准则对应的临界状态实际包括了木材的裂纹扩展过程，为区分起裂和扩展，日本学者Yoshihara[32]提出了以下木材复合断裂准则

2 木材复合型断裂试验

2.1 木材I型和II型断裂韧度的试验确定

在木材复合型断裂准则中至少需要确定KIc，一些断裂准则还需要确定KIIc.因此断裂试验就涉及到这两个断裂韧度的确定.双悬臂梁DCB(double cantilever beam)或锥形双悬臂梁 TDCB(tapered double cantilever beam)是目前对于木材I型断裂韧度KIc确定常用的方法[34-36]，日本工业标准(Japanese Industrial Standard,JIS)规定了DCB方法测试纤维增强材料断裂韧度的标准[37].对于II型断裂，可采用紧凑受剪试件CS(compact shear)，如图6(a)所示[13,38-39]，这种试件是1977年提出的用于各向同性材料的[40].但计算发现I型断裂占II型的10%，因此CS试件不能认为是纯II型断裂.

端部缺口受弯ENF(end-notched flexure)试件是1977年Barrett等[41]提出的试件形式，也是目前研究木材 II型断裂试验常用的试件形式[42-44]. ENF是在受弯构件中性轴处预制裂纹，因为在中性轴处，剪应力存在而正应力为零，保证裂纹尖端处于II型状态，而且这种试件的应力强度因子有明确的数学公式表示.但这种试件缺点是,由于裂纹有闭合的趋势，从而上下裂纹面受到摩擦力的影响.如果为避免摩擦力影响而在裂缝面处放置金属滚轴的话，则可能受到I型裂纹的影响.

1982年，Hunt等[12]提出采用复合断裂模式试验测定KIIc，如图6(b)所示.这种模式的优点是裂纹尖端应力强度因子与外载荷的关系已知，无需有限元计算；另外，比较容易实现纯I和纯II型加载.

2008年日本学者Yoshihara[45]提出了四点弯曲缺口梁试件，如图6(c)所示.在缺口平面内，只有剪应力存在，弯矩为零，而且避免了ENF试件存在的问题.其实，用于测试KIc和KIIc的试验方法还有很多，但考虑到本文主要是针对复合型裂纹，而大部分木材复合断裂准则KIIc不是必要的断裂参数，因为我们主要介绍木材复合型断裂试验方法，即KI和KII同时存在的情况.

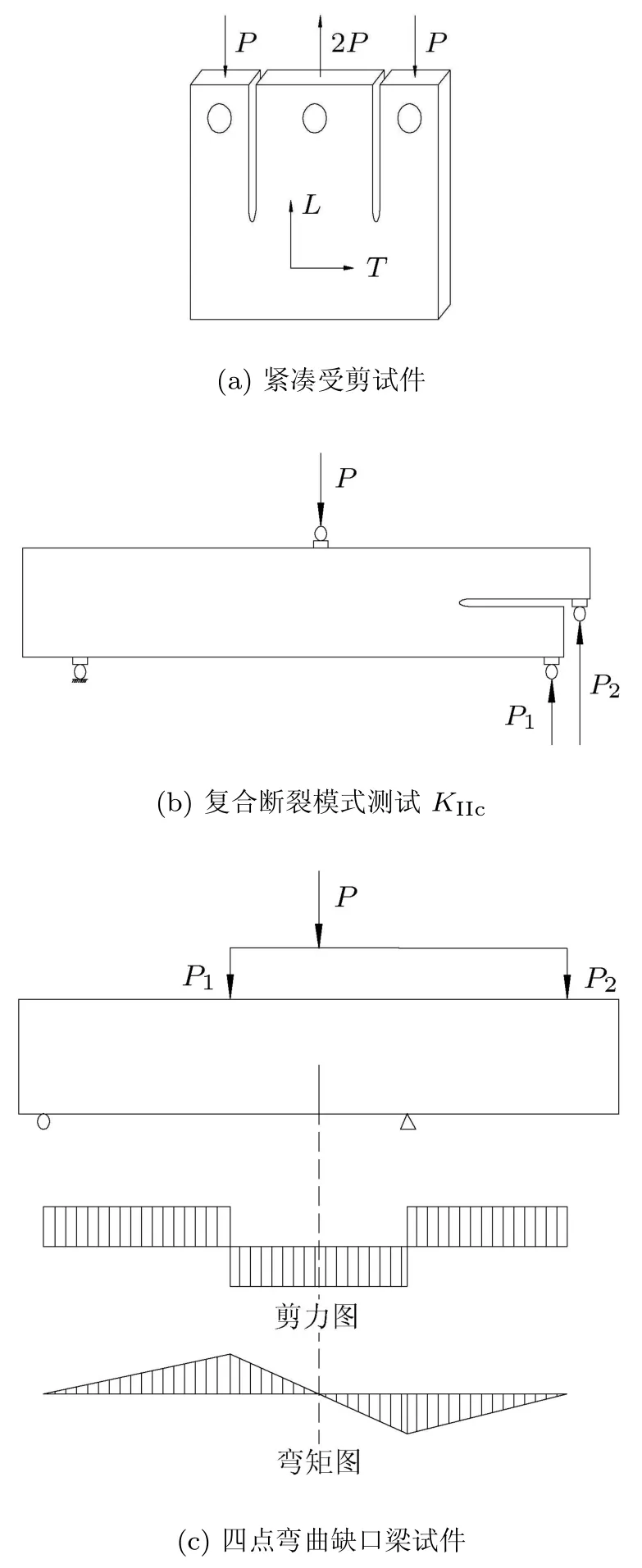
图6 不同试件测试KIIc

2.2 木材复合型断裂试验方法

虽然研究人员进行了很多木材的复合断裂研究，但到目前为止还没有一个较为统一的模式.这里我们选取几类常见的几何形式介绍.

Wu[9]在 1967年研究巴沙木 I/II复合型试验时采用了自重测试装置模拟无限尺寸大板的中心裂纹，实现 I型、II型以及复合型加载.对于无限大板，由于初始裂纹方向与L方向一致，因此裂纹尖端的应力强度因子计算公式直接采用各向同性材料的.

木材复合断裂试验亦可采用单边裂纹，裂纹初始方向与加载方向有一定的角度，保证裂纹尖端的复合断裂，如图 7(a)所示. 文献 [11,13,17]采用单边裂纹试件进行了复合断裂试验.这种试件裂纹尖端的应力强度因子计算需通过有限元实现，另外KII/KI的比例范围有限.比如文献[11]采用最大角度θ=75°时，KII/KI=3.5，而文献[13]采用最大角度θ=85°时，KII/KI=2.35.对于文献[17]，最大角度取θ=45°时，KII/KI的值还不超过1.因此单边裂纹不能得到完整的KI-KII曲线，或者说仅由单边裂纹断裂试件得到的结论具有局限性.因此文献[13]还采用了中心裂纹试件来弥补单边裂纹试件的不足，如图7(b)所示.在中心裂纹最大角度θ=85°时，有限元计算可得KII/KI=7.27.

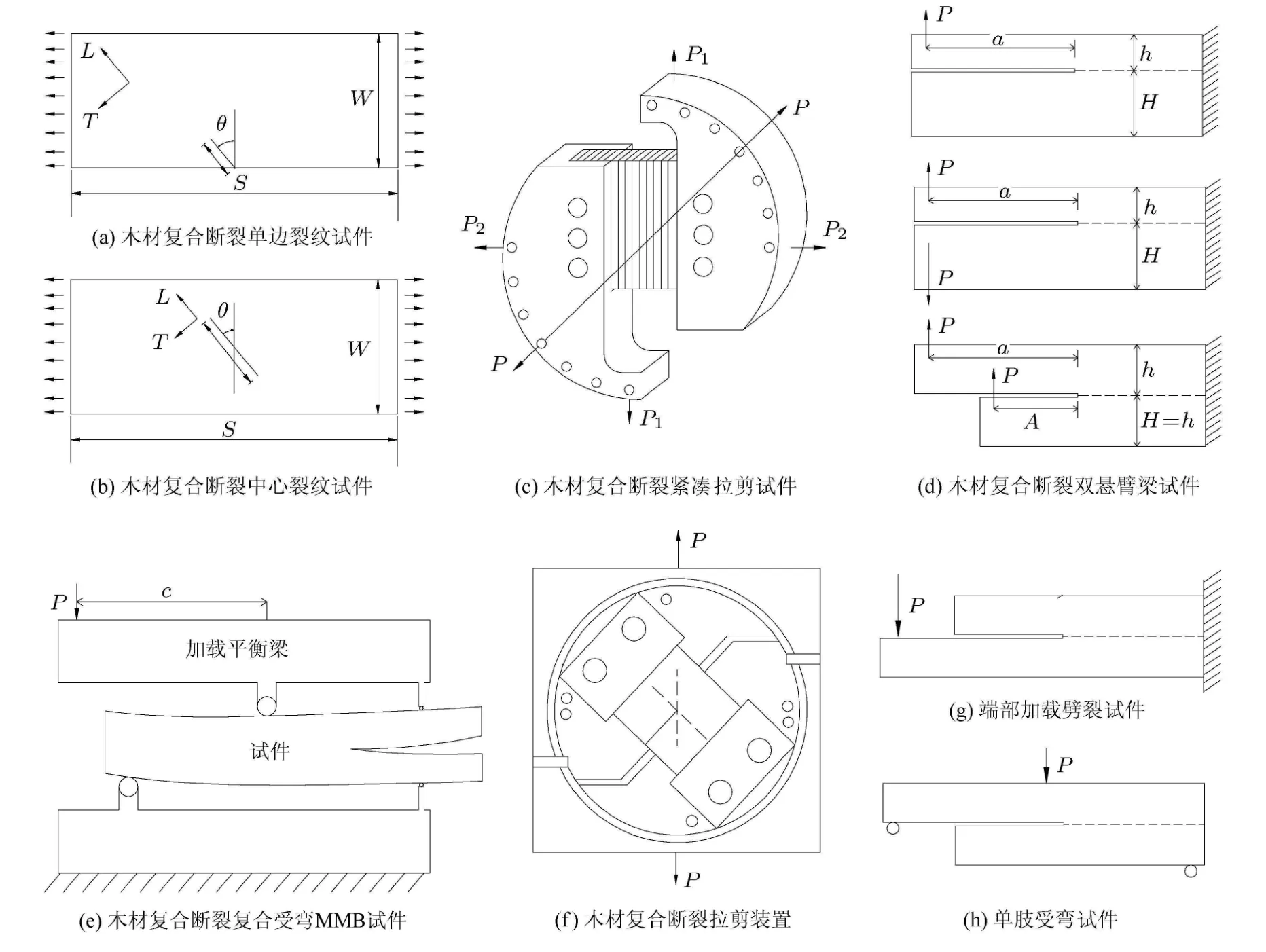
图7 木材复合型断裂试验方法

1989年 Valentin等[46]提出了紧凑拉剪试件CTS(compact tension shear)用于木材复合断裂试验，见图 7(c).通过改变载荷与纤维方向夹角可以实现不同的KI与KII组合.这种试件的优势是可以轻松满足纯I、纯II和复合型断裂条件，而且在纯II型状态下，I型的影响小于1%,可以忽略；另外,裂纹的制作相对容易.但应注意的是，由于这种试件对材料参数比较敏感，因此对每组正交材料的常数都要进行应力强度因子校正.

早在1992年Bao等[47]提出采用双悬臂梁进行正交材料的复合断裂.2001年Jernkvist[17]进行挪威松复合断裂时采用了双悬臂梁DCB试件，如图7(d)所示.通过变化h/H的相对大小实现KII/KI比例较小的情况；通过变化a/A实现较大KII/KI比例的情况.双悬臂梁的一个优势是裂纹尖端的应力强度因子不用通过有限元计算，通过简单的梁理论就可推导出来.另外DCB可实现纯I和纯II型断裂.但DCB试件裂纹尖端的T应力数值较大，其影响不能忽略.

2001年 Tschegg等[48]提出了楔入劈拉试件用于木材复合断裂试验，原理与混凝土的楔入劈拉试验相同，但是通过不对称的楔入装置实现I/II复合断裂，并通过较大角度的楔入装置实现大比例的KII/KI的效果.

复合受弯MMB(mixed-mode bending)试件最初用于复合材料的分层试验[49]. 2007年有学者采用复合受弯 MMB[49]试件研究了木材的复合断裂[30,50-51]，如图7(e)所示.日本学者Yoshihara[32]也用MMB试件研究了木材复合起裂和扩展条件.这类试件的3个优势：(1)较容易实现KII/KI不同比例情况；(2)结合了适用I型的DCB和II型的ENF试件的优势，裂纹尖端的应力强度因子可以用简单梁理论推导；(3)可以实现裂纹的稳定扩展.

2008年Romanowicz等[22]为验证非局部应力断裂准则时，采用了文献[52]提出的复合拉剪加载装置，如图7(f)所示.实际上这个加载与Valentin和Caumes在1989年提出的紧凑拉剪CTS试件原理一致，只不过这类试件初始裂纹方向与纤维L方向的夹角也随着变化.另外，为避免边界的约束效应，在加载装置和测试试件之间进行了改进，在试件两端粘贴了一定长度的试件材料，其纤维方向与受拉方向平行.另外，与CTS原理一致的还有Arcan加载装置也可用于木材复合断裂试验[53-54].

2009年 Oliveira等[55]讨论了端部加载劈裂ELS(end loaded split)试件和单肢受弯SLB(singleleg bending)试件，如图7(g)和图7(h)所示.虽然两类试件产生的KII/KI比例有限，但与MMB试件相比，两类试件操作简单，试验设备也不复杂.如SLB和常规三点弯曲梁设置是相同的，而ELS只需要一个夹持固定装置.另外，裂纹尖端的应力强度因子等断裂参数也可直接推导，无需复杂的有限元计算.

3 结论和展望

我国对木材断裂行为研究起步晚，北京林业大学的鹿振友[56]在 1988年首次发表了介绍木材断裂力学在国外研究进展的文章，其后高校以及科研机构在木材断裂方面进行了一些基础的研究工作[57-59].安徽农业大学的邵卓平比较系统地研究了木材的断裂行为，并在2012年出版了专著《植物材料(木、竹)断裂力学》[60]，将其十多年的研究成果汇聚成册，为推广断裂力学在木材上的应用提供了理论依据.但总体说来，我国木材断裂力学的研究还主要集中在I型裂纹，包括顺纹和横纹扩展，而对木材复合型裂纹的研究还基本属于空白.复合型裂纹是木材实际断裂过程中出现的真实受力状态，因此本文的介绍希望能帮助研究同行了解国外在木材复合型断裂的研究现状，对以后的研究方向和重点提供一些思考.

(1)虽然木材裂纹扩展可能有8种模式，但由于各个方向强度以及断裂韧度的巨大差别，有些裂纹模式几乎不出现，比如LR和LT.即使有跨过纤维的裂纹，在扩展时也会沿着纤维方向.因此木材复合型断裂研究更多地集中在RL或者TL模式上.

(2)木材I/II复合型裂纹扩展基本都沿着纤维方向，因此不需要预测裂纹扩展角度，而只需建立复合型裂纹扩展的条件.这点与各向同性材料是不同的.

(3)除I/II复合型外，木材复合型断裂还可能出现I/III,II/III或者三者同时存在.对这几种情况研究得很少.在2008年有研究人员采用拉扭圆柱体试件进行了云杉和山毛榉的I/III复合型断裂研究[61].

(4)在计算木材断裂韧度时，存在对极限载荷的定义问题.早期的断裂模型将木材处理为线弹性材料，即最大载荷对应线弹性破坏极值点.但有些研究人员认为木材是类似混凝土的准脆性材料，其裂纹的扩展要经过稳定扩展阶段，因此起裂载荷对应线弹性极限点，而最大载荷对应裂纹不稳定扩展.据此，木材的复合型断裂破坏面也分为起裂阶段和裂纹扩展阶段.

(5)木材复合型断裂主要集中在KI＞0的情况，但在实际工程中木材可能会处于压剪状态，即裂纹闭合的情况.由于裂纹闭合会存在裂纹面间的摩擦力，对II型断裂有影响.另外，负的应力强度因子是否存在，物理意义如何解释，这些都是我们今后应该解决的问题.

(6)裂缝尖端T应力的影响还没有引起足够的认识.在各向同性材料中，当T应力与应力强度因子比较大时，将对裂纹扩展方向和扩展条件产生明显的影响.而对各向异性材料研究成果较少.在文献[62]中，Su和Sun采用分形有限元方法计算了各向异性材料裂纹尖端的应力强度因子和T应力.具体到木材而言，T应力对裂纹扩展的影响还需进一步研究.

(7)在各向同性材料中，对于四点弯曲缺口梁，在弯矩为零的缺口平面内，存在I型开裂的模式[63].对于各向异性的木材是否存在这种问题，值得进一步思考.

(8)本文主要介绍原木的复合型断裂，而胶合木作为主要的工业木产品，其断裂研究还处于起步阶段.胶合木的断裂破坏可能发生在层内，原理同原木.但也可能发生在胶合木的层间，断裂就要复杂一些，胶合木的层间断裂是我们目前正在从事的研究工作.

1 European Committee for Standardization.EN 1995-1-1 Design of Timber Structures.Part 1-1：general rules and rules for buildings.Brussels：European Committee for Standardization(CEN),2004

2 CSA 086-01 Engineering Design of Wood.Toronto：Canadian Standard Association(CSA),2001

3 GB50005-2003木结构设计规范.北京：中国建筑工业出版社, 2003

4 Porter AW.On the mechanics of fracture in wood.Forest Products Journal,1964,14(8)：325-331

5 Erdogan F,Sih GC.On the crack extension in plates under plane loading and transverse shear.Journal of Basic Engineering,1963,85(5)：19-27

6 Nuismer RJ.An energy release rate criterion for mixed mode fracture.International Journal of Fracture,1975, 11(12)：245-250

7 Sih GC.Strain-energy-density factor applied to mixed mode crack problems.International Journal of Fracture, 1974,10(3)：305-321

8 Ashby MF,Easterling KE,Harrysson R,et al.The fracture and toughness of woods.Proceedings of the Royal Society of London A,1985,398：261-280

9 Wu EM.Application of fracture mechanics to anisotropic plates.Journal of Applied Mechanics,1967,34(4)：967-974

10 Leicester RH.Application of linear fracture mechanics in the design of timber structures. Conference Australian Fractured Group 23,Melbourne,Australian,1974

11 WilliamsJG,BirchMW.Mixed modefracturein anisotropic media.Cracks and Fracture STP601,American Society for Testing and Materials,Philadelphia,USA, 1976

12 Hunt DG,Croager WP.Mode II fracture toughness of wood measured by a mixed-mode test method.Journal of Materials Science Letter,1982,1：77-79

13 Mall S,Murphy JF,Shottafer JE.Criterion for mixed mode fracture in wood.Journal of Engineering Mechanics,1983, 109(3)：680-690

14 Chan SK,Tuba IS,Wilson WK.On the f i nite element method in linear fracture mechanics.Engineering Fracture Mechanics,1970,2(1)：77-85

15 Buczek MB,Herakovich CT.A normal stress criterion for crack extension direction in orthotropic composite materials.Journal of Composite Materials,1985,19：544-553

16 Jernkvist LO.Fracture of wood under mixed mode loading I.Derivation of fracture criterion.Engineering Fracture Mechanics,2001,68：549-563

17 Jernkvist LO.Fracture of wood under mixed mode loading II.Experimental investigation of Picea abies.Engineering Fracture Mechanics,2001,68：565-576

18 赵艳华,陈晋,张华.T应力对I/II复合型裂纹扩展的影响.工程力学,2010,27(4)：5-12

19 Smith DG,Ayatollahi MR,Pavier MJ.On the consequences of T-stress in elastic brittle fracture.Proceedings of the Royal Society of London A,2006,462：2415-2437

20 Shahani AR,Tabatabaei SA.Ef f ect of T-stress on the fracture of a four point bend specimen.Materials and Design, 2009,30：2630-2635

21 van der Put TACM.A new fracture mechanics theory for orthotropic materials like wood.Engineering Fracture Mechanics,2007,74：771-781

22 Romanowicz M,Seweryn A.Verif i cation of a non-local stress criterion for mixed mode fracture in wood.Engineering Fracture Mechanics,2008,75：3141-3160

23 Mroz Z,Seweryn A.Non-local failure and damage evolution rule：application to a dilatant crack model.Journal de Physique IV,1998,8：257-268

24 Gowhari-Anaraki AR,Fakoor M.Mixed mode fracture criterion for wood based on a reinforcement microcrack damage model.Materials Science and Engineering A,2010, 527：7184-7191

25 Gowhari-Anaraki AR,Fakoor M.General mixed mode I/II fracture criterion for wood considering T-stress ef f ects.Materials and Design,2010,31：4461-4469

26 Gowhari-Anaraki AR,Fakoor M.A new mixed-mode fracture criterion for orthotropic materials,based on strength properties.The Journal of Strain Analysis for Engineering Design,2011,46：33-44

27 Yuan FG.Fracture behavior of a stitched wrap-knit carbon fabric composite.NASA/TM-2001-210868,Washington,DC,2001

28 Fakoor M,Raf i ee R.Fracture investigation of wood under mixed mode I/II loading based on the maximum shear stress criterion.Strength of Materials,2013,45(3)：378-385

29 Bodig J,Jayne BA.Mechanics of Wood and Wood Composite.New York：Van Nostrand Reinhold Company,1982

30 de Moura MFSF,Oliveira JMQ,Morais JJL,et al.Mixedmode I/II wood fracture characterization using the mixedmode bending test.Engineering Fracture Mechanics,2010, 77：144-152

31 Benzeggagh ML,Kenane M.Measurement of mixedmode delamination fracture toughness of unidirectional glass/eposy composites with mixed-mode bending apparatus.Composites Science Technology,1996,56：439-449

32 Yoshihara H.Initiation and propagation fracture toughness of solid wood under mixed mode I/II condition examed by mixed-mode bending test.Engineering Fracture Mechanics,2013,104：1-15

33 Kossakowski PG.Mixed mode I/II fracture toughness of pine wood.Archives of Civil Engineering,2009,5(2)：199-227

34 de Moura MFSF,Morais JJL,Dourado N.A new data reduction scheme for mode I wood fracture characterizationusing the double cantilever beam test.Engineering Fracture Mechanics,2008,75：3852-3865

35 Yoshihara H,Kawamura T.Mode I fracture toughness estimation of wood by DCB test.Composites:Part A,2006, 37：2105-2113

36 Coureau J,Morel S,Durado N.Cohesive zone model and quasibrittle failure of wood：a new light on the adapted specimen geometries for fracture tests.Engineering Fracture Mechanics,2013,109：328-340

37 JIS K7086-93.Testing Method for Interlaminar Fracture Toughness of Carbon Fibre Reinforced Plastics.Tokyo：Japanese Industrial Standards Group,1998

38 Valentin GH,Morlier P.Toughness of timber：experimental determination ofKIc,KIIcandJc.5th International Conference of Fracture,Paper 249,Cannes,France,1981

39 Cramer SM,Pugel AD.Compact shear specimen for wood mode II fracture investigation.International Journal of Fracture,1987,35：163-174

40 Chisholm DB,Jones DL.An analytical and experimental stress analysis of a practical model II fracture test specimen.Experimental Mechanics,1977,1(1)：7-13

41 Barrett JD,Foschi RO.Mode II stress-intensity factors for cracked wood beams.Engineering Fracture Mechanics,1977,9：371-378

42 Yoshihara H.Mode II initiation fracture toughness analysis for wood obtained by 3-ENF test.Composites Science and Technology,2005,65：2198-2207

43 Yoshihara H.Theoretical analysis of 4-ENF tests for mode II fracturing in wood by f i nite element method.Engineering Fracture Mechanics,2008,75：290-296

44 Yoshihara H,Satho A.Shear and crack tip deformation correction for the double cantilever beam and three-point-endnotched specimens for mode I and mode II fracture toughness measurement of wood.Engineering Fracture Mechanics,2009,76：335-346.

45 Yoshihara H.Mode II fracture mechanics properties of wood measured by the asymmetric four-point bending test using a single-edge-notched specimen.Engineering Fracture Mechanics,2008,75：4727-4739

46 Valentin G,Caumes P.Crack propagation in mixed mode in wood：a new specimen.Wood Science Technology,1989, 23：43-53

47 Bao G,Ho S,Suo Z,et al.The role of material orthotropy in fracture specimens for composites.International Journal of Solids Structures,1992,29(9)：1105-1116

48 Tschegg EK,Reiterer A,Pleschberger T,et al.Mixed mode fracture energy of sprucewood.Journal of Materials Science,2001,36：3531-3537

49 Reeder JR,Crews JH.Mixed-mode bending method for delamination testing.American Institute of Aeronautics and Astronautics Journal,1990,28(7)：1270-1276

50 Oliveira JMQ,de Moura MFSF,Morais JJL.Numerical analysis of the MMB test for mixed-mode I/II wood fracture.Composite Science Technology,2007,67：1764-1771

51 de Moura MFSF,Oliveira JMQ,Morais JJL,et al.Mixedmode(I+II)fracture characterization of wood bonded joints.Construction and Building Materials,2011,25：1956-1962

52 Seweryn A,Poskrobko S,Mr´o Z.Brittle fracture in plane elements with sharp notches under mixed mode loading.Journal of Engineering Mechanics,1997,123：535-543

53 M´eit´e M,Dubois F,Pop O,et al.Mixed mode fracture properties characterization for wood by digital images correlation and f i nite element method coupling.Engineering Fracture Mechanics,2013,105：86-100

54 Pop O,Moutou-Pitti R,Dubois F.Mixed-mode crack growth in wood.Pro Ligno,2012,8(3)：12-18

55 Oliveira JMQ,de Moura MFSF,Morais JJL.Application of the end loaded split and single-leg bending tests to the mixed-mode fracture characterization of wood.Holzforschung,2009,63：597-602

56 鹿振友.断裂力学在木材加工上的应用.北京林业大学学报, 1988,10(3)：49-56

57 范文英,徐虹,龚蒙.木材断裂韧性KIc测定方法的研究.南京林业大学学报,1993,17(3)：80-82

58 孙艳玲,鹿振友.用有限元计算水曲柳裂纹尖端应力强度因子.北京林业大学学报,1999,21(3)：53-57

59 田振农，张乐文.木材的宏观力学模型及断裂机理.北京林业大学学报,2010,32(2)：153-156

60 邵卓平.植物材料(木、竹)断裂力学.北京：科学出版社,2012

61 Loidl D,Tschegg EK,Stanzl-Tschegg SE.Fracturing of wood under superimposed tension and torsion.Wood Science Technology,2008,42：61-74

62 Su RKL,Sun HY.A brief note on elasticT-stress for centred crack in anistropic plate.International Journal of Fracture,2005,131(1)：53-58

63 He MY,Hutchinson JW.Asymmetric four-point crack specimen.Journal of Applied Mechanics,2000,67：207-209

(责任编辑：胡 漫)

A STATE-OF-THE-ART REVIEW OF FAILURE OF WOOD UNDER I/II MIXED MODE FRACTURE1)

ZHAO Yanhua∗,2)LI Zheng∗CHANG Jianmei∗,†
∗(State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116024,Liaoning,China)
†(Transportation Institute,Inner Mongolia University,Hohhot 010070,China)

For the design and the safety assessment of wood structures,an adequate knowledge of wood fracture behavior is important.Due to the complexity in its structure,wood is naturally anisotropic in the macroscopic scale,which makes it more difficult to study wood failure based on fracture mechanics than to study isotropic materials.Therefore,only fractures of pure mode I and pure mode II were given a considerable attention. Wood structural members are,however,often subject to the mixed mode fracture in reality,and the mixed mode fracture is now one of hot topics in the fracture studies.This paper gives a literature review on the wood mixed fracture from two aspects：the fracture criterion and the testing method.After an introduction of some empirical and physical models to predict the mixed mode fracture failure of wood,a comparison is made among these models using the test data in the literature.Various test methods are reviewed,with focus on fractures of mode I and mode II combined.Some issues for future studies are highlighted.

wood,fracture mechanics,mixed mode fracture,stress intensity factor,energy release rate

O346.1,TU502

A

10.6052/1000-0879-15-238

2015-10-09收到第1稿，2016-01-29收到修改稿.

1)中央高校基本科研业务费专项资金(DUT14LK38)和国家重点基础研究发展计划(2015CB057703)资助.

2)赵艳华，副教授，从事混凝土和木材断裂力学研究.E-mail：yanhuazh@dlut.edu.cn

赵艳华,李征,常建梅.木材I/II复合型断裂破坏研究进展.力学与实践,2017,39(1)：7-17

Zhao Yanhua,Li Zheng,Chang Jianmei.A state-of-the-art review of failure of wood under I/II mixed mode fracture.Mechanics in Engineering,2017,39(1)：7-17