砖砌体双参数单轴受压弹塑性损伤力学模型1)

牛力军 张文芳

(太原理工大学建筑与土木工程学院，太原030024)

砖砌体双参数单轴受压弹塑性损伤力学模型1)

牛力军2)张文芳3)

(太原理工大学建筑与土木工程学院，太原030024)

参考弹塑性损伤模型理论和相关试验数据，建立了砖砌体单轴单调受压和重复受压两种弹塑性损伤本构模型.在模型中采用抗压强度和峰值压应变双参数来调整形变曲线，从而实现了砖砌体单轴受压本构模型的精细化建立.模型不但与既有弹塑性模型相符，而且还符合受压延性与强度呈反向变化的试验结论.重复受压加-卸载路径建立在卸载线性假定的基础上，参考两组试验数据，得出了双线性抗压刚度劣化函数，并通过强度线性插值来调整劣化速率，从而建立了随强度改变的受压加-卸载损伤本构模型.

砖砌体，本构模型，损伤演变，重复载荷，数值模拟

引言

砌体结构是由块体和砂浆砌筑而成，其材料力学性能和损伤机理相当复杂，因而数值建模也较为困难.总的来说，对砌体建模的思路有两种，一种是分离式建模，一种是整体式建模.整体模型按照砌体的整体力学性能建立数值模型，该模型建模简单，所需计算资源较少，适用于整个结构的分析.目前对于砌体材料的整体模型有多种不同的研究方向，如考虑不同材料、不同组砌方式对弹塑性本构模型的敏感性研究[1]，采用弯矩-截面曲率模型来预测砌体受压行为[2].当采用整体模型时，砌体轴心受压本构关系是最基础的材料力学参数.现有的带损伤变量的砖砌体弹塑性受压本构模型较少，如将砌体全部细观单元破坏应变认为是一个均匀随机场，利用概率理论方法建立基于应变的损伤本构模型[3].大多数受压弹塑性模型不含损伤变量，仅采用单一的应力-应变函数表达，虽然可以反映材料的应力-应变关系，但是不能直接反映砖砌体的受压损伤状态，数值求解效率不高.砖砌体轴心受压除单调加载外，还存在往复加载情况，目前已有一些砖砌体试件的重复受压加卸载试验[4]，但是理论模型较少.本文根据损伤模型理论，建立了单调受压和重复受压两种本构模型.根据抗压强度、峰值压应变与损伤演变进程之间的逻辑关系，在本构模型中采用抗压强度和峰值压应变双参数来调整形变曲线，从而实现了砖砌体单轴受压本构模型的精细化建立.

1 弹塑性损伤模型简介

弹塑性损伤模型最早由Kachanov首先提出，经过发展衍生出多种表达形式，如式(1)和式(2)[5-6]

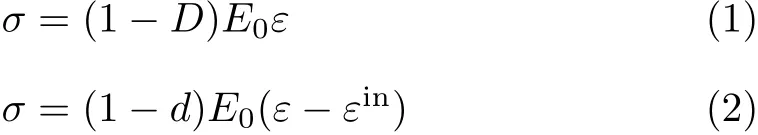
式中，E0为初始弹性模量；εin为非弹性应变,εin=.式(1)本构模型见图1所示，式中D定义为单轴受压损伤演化参数，物理意义为原点割线模量的退化率，该本构模型的特征是直接采用单标量的形式来表征刚度演化，物理意义清晰，应力表达简单.式(2)本构模型见图2所示，式中d定义为单轴受压损伤变量，假定卸载-再加载路径为直线，则损伤变量的物理意义为卸载路径斜率的退化率，该模型的特征是将总应变进行如下分解

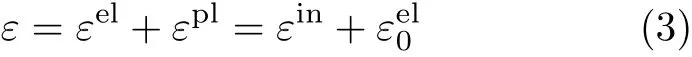
式中，εpl为塑性应变；εel为弹性应变；为卸载时按照初始弹性模量计算的应变.

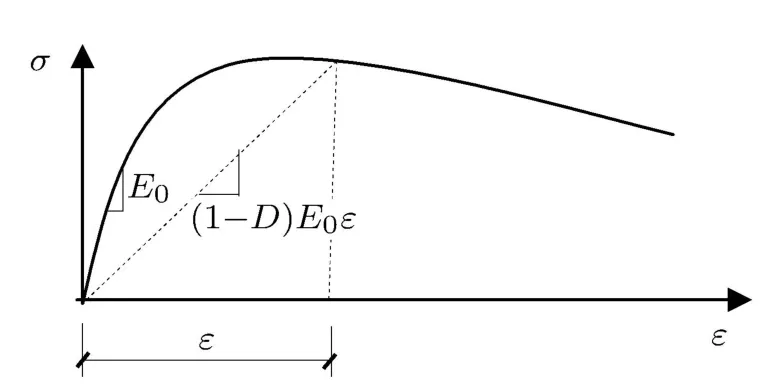
图1 式(1)应力-应变理论模型

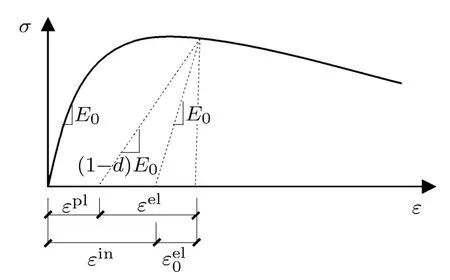
图2 式(2)应力-应变理论模型

式(2)本构模型将损伤演化和塑性变形解耦,不但可以提高数值算法的计算效率，易于求解结果的收敛，而且在应力-应变曲线中包含了卸载 -再加载的应力表达.在该模型的基础上发展出混凝土塑性损伤模型，它可以用来分析准脆性材料如混凝土、岩石和砂浆等，亦可用来分析砌体材料.

上述两种塑性损伤模型通过不同的损伤参数表征材料的力学性能劣化程度，力学机理明确，在数值求解方面优于传统的弹塑性模型.

2 单调受压弹塑性损伤模型

2.1 既有的砖砌体弹塑性本构模型

砖砌体轴压试验多采用 5皮砖棱柱体试件进行，如文献 [7]对 40组 5皮砖试件进行的轴压试验，其典型试验曲线见图3.图中Em和fm分别为砌体的弹性模量与抗压强度.大量的砖砌体轴压试验均表现出图3类似的形变特征，即随着砌体强度的改变，受压形变曲线显著变化，延性、峰值应变均与强度呈反向变化[8].

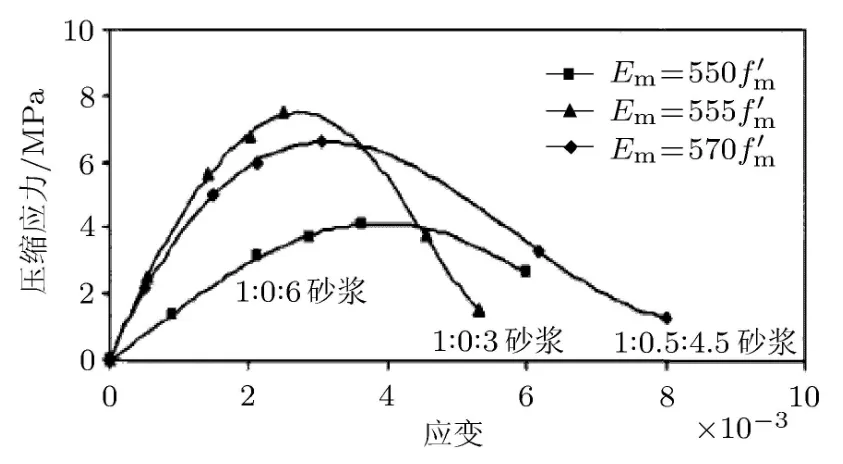
图3 文献[7]砖砌体轴压试验曲线

现有的砖砌体弹塑性模型多将峰值应力、峰值应变作为无量纲化阈值，构建统一的本构曲线，表1为几个不同函数类型的本构表达[9-10].

表1 砌体受压应力-应变关系表达式

上述表达式有指数函数、多项式和方程式分段等形式，除此之外，还有一些学者提出了直线型、对数函数型等形式.现有的砖砌体本构模型研究虽较多，但多数都是单标量弹塑性形式，不能反映材料的损伤演变特征，也不能反映不同强度、不同峰值应变时曲线形状变形特征.

2.2 单调受压弹塑性损伤模型

砖砌体轴心受压损伤在前期可认为是内部微观裂缝发展引起的,后期由于裂缝的贯通，依靠残余承压面和裂缝之间的咬合力来承担轴力，此时损伤模型可简化为几个裂缝间的独立小柱，其横截面积为残余承压面，裂缝面积为损伤面积.砌体轴心受压损伤过程,可采用Robotnov[11]经典损伤力学损伤演化参数.

式中，Ad为细观损伤单元面积，即砌体退出工作的横截面面积；A为无损砌体的横截面积.

采用式(4)定义损伤演化参数后，可采用式(1)建立砖砌体塑性损伤本构模型.损伤演化参数为式(1)应力表达中的控制指标，其取值是本构模型的关键.由于砖砌体与混凝土具有类似的受压本构曲线，本文参考既有混凝土损伤演化参数，通过与砖砌体曲线的对比，确定砖砌体该参数取值.文献[12]中的混凝土单轴受压损伤演化参数为

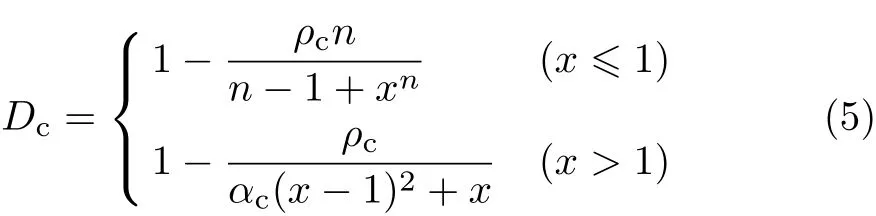
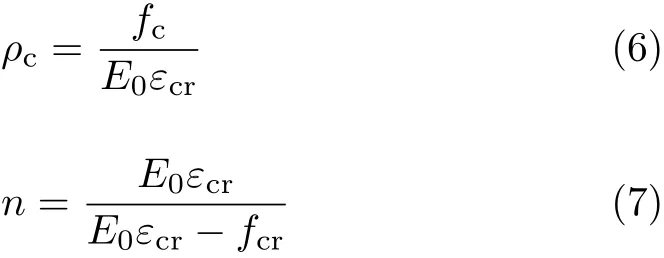
式中,Dc为混凝土单轴受压损伤演化参数,本文取其作为砖砌体损伤演化参数，即式(4)中D值；αc为混凝土单轴受压应力-应变曲线下降段参数值，取值见文献[12]；fcr为混凝土单轴抗压强度代表值，根据实际结构分析的需要选取；εcr为与单轴抗压强度fcr相应的混凝土峰值压应变.

上述公式中αc按低强度混凝土取0.74，峰值压应变取0.003，E0=1600fc，求解损伤演化参数D值，并代入式(1)得到的砖砌体受压本构曲线与表1曲线对比见图4，图4曲线区间参考其他文献取到 1.6ε0点.由图 4可知，采用式 (5)计算的损伤演化参数，按照式(1)得出的本构曲线与其他弹塑性模型曲线路径相符，说明低强度混凝土的损伤演化参数符合砖砌体轴心受压损伤演变特征，可采用其公式计算砖砌体D值.式(5)采用了强度与峰值压应变双变量来计算D值，强度越高，峰值压应变越小，刚度劣化则越快.砖砌体本构曲线在1.6ε0和0.5fc区间可假定为直线下降段，并假定0.5fc对应应变为nε0,其中n为实常数，经过与试验对比，本文建议取n=2.4.本构曲线过0.5fc应力点后，材料损伤受围压影响显著，可根据求解收敛性和边界条件等情况设置下降路径.按上述损伤模型模拟图3试验的理论曲线见图5.图5模拟曲线与图3试验曲线形态类似，符合强度、峰值压应变与损伤演变进程之间的逻辑关系，说明本文按式(1)建立的弹塑性损伤模型较表1单标量本构模型更为合理和适用.

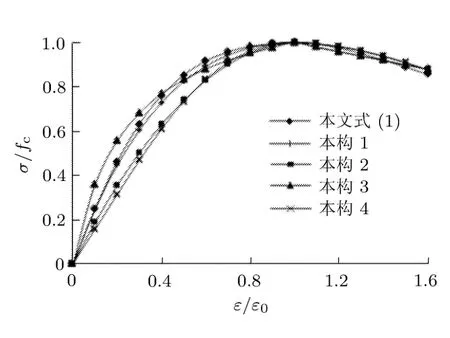
图4 损伤模型与其他弹塑性模型的对比图

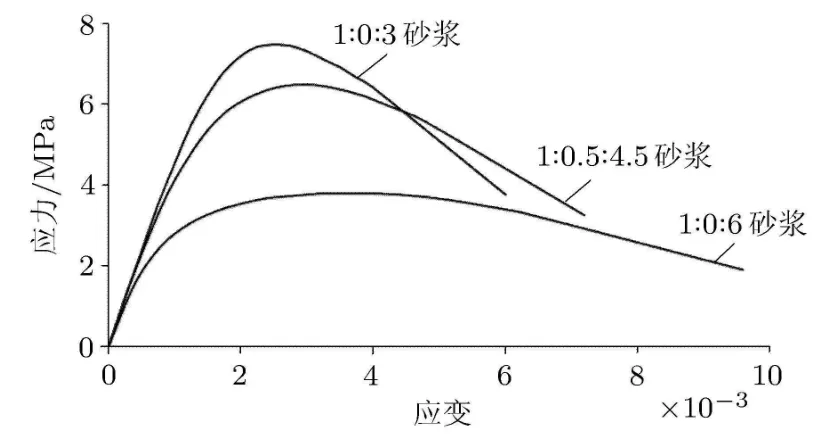
图5 损伤模型本构曲线

3 重复受压弹塑性损伤模型

3.1 棱柱体砖试件重复受压加卸载试验

无筋砌体重复受压加卸载试验数据较少，现以文献中两组轴心受压试验为依据，分析砖砌体轴压卸载刚度特征.两组试验分别采用黏土砖和灰砂砖，砂浆分别采用水泥砂浆和混合砂浆(水泥：石灰：砂为1：0.5：4).两组试验主要情况见表2[13-15].

重复加卸载试验曲线的外包线可认为与单轴受压本构曲线基本重合，文献[13]和文献[15]重复加卸载曲线的外包线有显著区别，也表现出强度与延性反向变化的特征.按照式(1)得到的两组试件本构模型见图6.图6曲线与试验外包线形状较为相符，再次验证了式(1)模型的适用性.

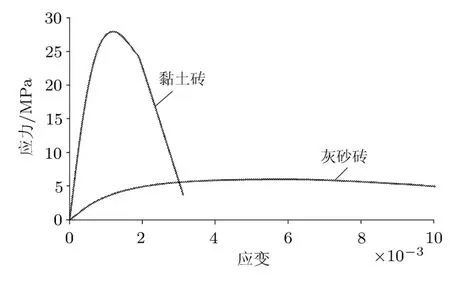
图6 损伤模型本构曲线

3.2 卸载路径与刚度劣化

式(2)弹塑性损伤模型包含重复加-卸载路径，其重复加-卸载路径为线性假定.基于表2两组试验数据，按照式(2)构建以无量纲化应变为自变量的卸载路径的本构关系，无量纲化应变仍采用峰值应变作为阈值.文献[15]已经给出了试验试件受压卸载刚度演变拟合函数，见式(9).本文根据文献[13]试验数据，也得出了相应的拟合函数，见图7.

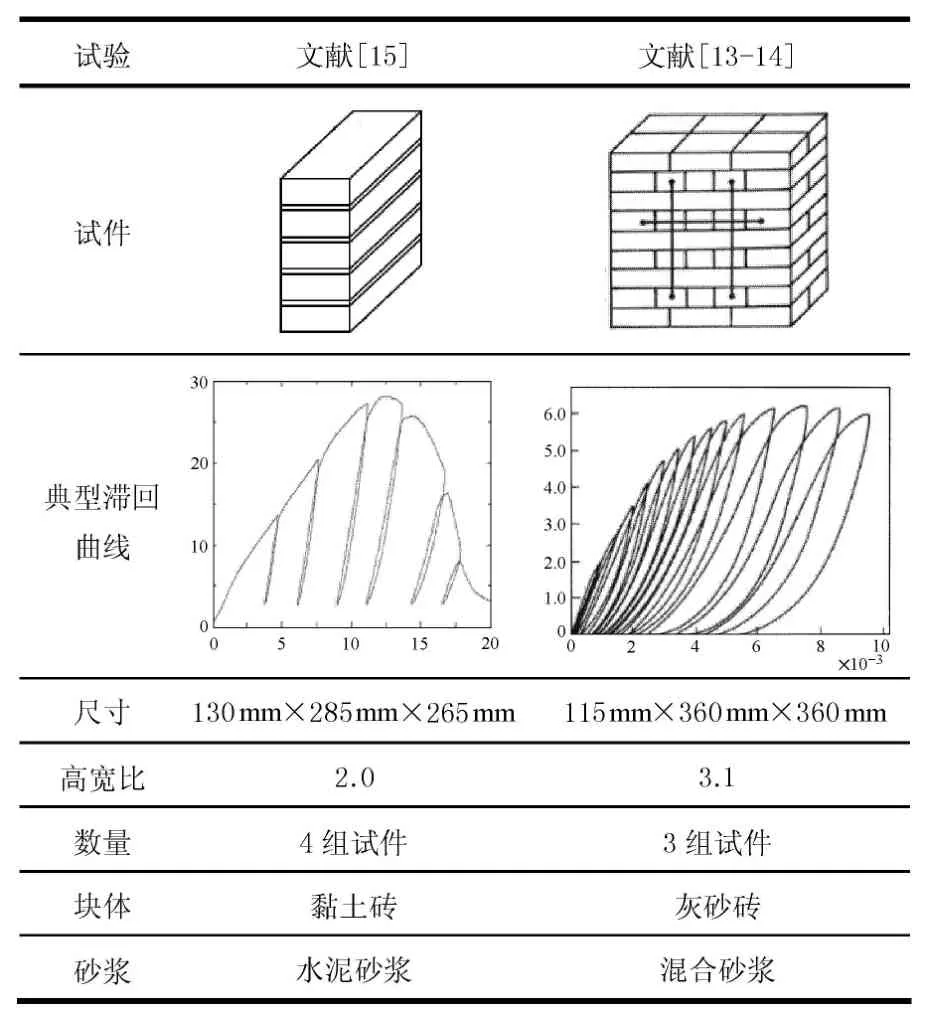
表2 重复受压加卸载试验表

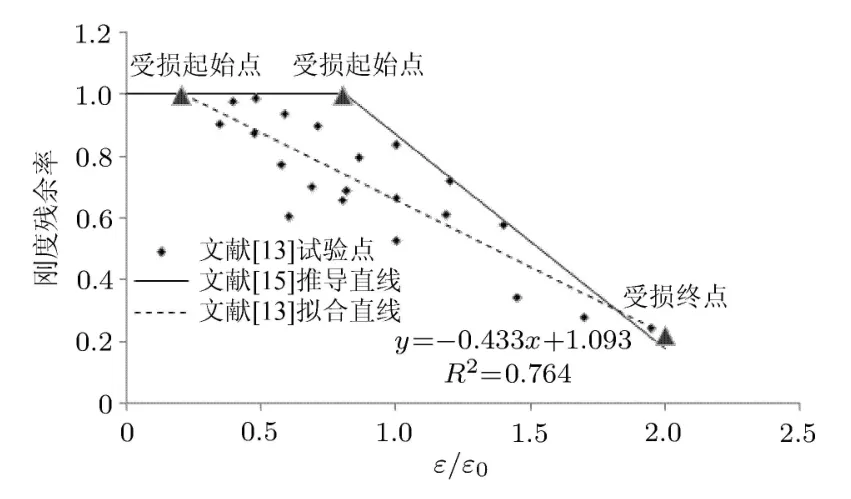
图7 刚度劣化拟合表达

由图7可知，砖砌体重复受压加-卸载刚度劣化可拟合为双线性，前期为无损阶段，两组试验受损起始点分别为0.2ε0和0.8ε0.损伤阶段均可拟合成线性函数，分别为式(8)和式(9).

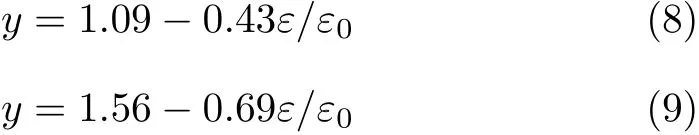
式中，y为重复加-卸载抗压刚度残余率.

砖砌体强度越高，则初始损伤对应无量纲化应变越大，且损伤后劣化速率快，受压脆性特征明显.当应变达到2ε0时，对应的刚度残余率均为0.2，刚度劣化已基本完成，在本构模型中可取该点作为受损终点.

3.3 式(2)弹塑性损伤模型

按照式(2)建立损伤模型时，损伤变量为

重复加-卸载抗压刚度残余率y按双线性取值，前期为无损阶段，受损起始点可按强度比例(6MPa～28MPa)在 0.2ε0和 0.8ε0之间线性内插.当受损终点取 (2ε0,0.2E0)时，则可根据受损起始点和受损终点建立刚度劣化线性函数.当强度小于6MPa时，y值可采取式(8)计算，当强度大于28MPa时，y值可采取式(9)计算.通过考虑强度和峰值压应变双变量对受损起始点和卸载抗压刚度劣化速率的影响，实现了砖砌体重复轴压本构模型的精细化建立.按照式 (2)重复轴压模型，采用ABAQUS数值程序中的混凝土塑性损伤模型对试验[13]的数值模拟见图 8，图中实线为试验曲线，虚线为模拟曲线.

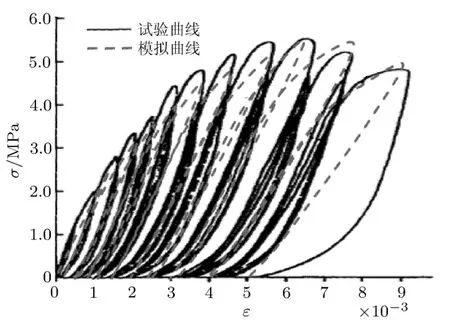
图8 重复轴压试验数值模拟结果

由图8可知，模拟曲线的捏拢性及卸载线性特征与试验有一定的区别，但加载外包线、卸载终点均与试验基本相符，说明该模型能够反映重复轴压力学行为特征，且建模实践发现采用损伤模型后滞回加载的计算效率有显著提高.

4 结 论

(1)本文采用抗压强度和峰值压应变作为损伤变量和损伤演化参数的双参数变量，分别构建了砖砌体单轴单调受压和重复受压弹塑性损伤模型，可以通过双参数的设置来调整两个本构模型的形变曲线，从而实现了材料模型的精细化建立.

(2)单调受压本构模型采用损伤演化参数控制损伤演化进程，该参数在 0～1.6ε0区间内分为上升段和下降段，均采用指数型函数表达；在1.6ε0～2.4ε0下降区间采用线性函数表达.单调本构模型不但与既有弹塑性本构模型相吻合，而且通过双参数的设置，体现了砖砌体强度越高，延性越低的材料力学特征.

(3)重复受压弹塑性损伤模型采用损伤变量控制卸载刚度，刚度劣化采用双线性函数表征.当强度在6MPa～28MPa区间时，受损起始点在0.2ε0～0.8ε0线性内插，从而调整了刚度劣化速率.数值模拟与试验曲线的对比表明，模拟曲线可基本反映材料的加-卸载形变特征.

1 Sousa R,Guedes J,Sousa H.Characterization of the uniaxial compression behaviour of unreinforced masonry-Sensitivity analysis based on a numerical and experimental approach.Archives of Civil and Mechanical Engineering, 2015,15(2)：532-547

2 Parisi F,Sabella G,Augenti N.Constitutive model selection for unreinforced masonry cross sections based on best-f i t analytical moment-curvature diagrams.Engineering Structures,2016,111：451-466

3 杨卫忠.砌体受压本构关系模型.建筑结构,2008,38(10)：80-82

4 Graziotti F,Rossi A,Mandirola M,et al.Experimental characterisation of calcium-silicate brick masonry for seismic Assessment.16th International Brick and Block Masonry Conference,Padova,Italy,2016

5 Kachanov LM.Time of the rupture process under creep conditions.Isv Akad Nauk SSR Otd Tekh Nauk,1958,8：26-31

6 Hibbitt K.ABAQUS user’s manuals version 6.3.Sorensen, Inc,2002

7 Kaushik HB,Rai DC,Jain SK.Stress-strain characteristics of clay brick masonry under uniaxial compression.Journal of Materials in Civil Engineering,2007,19(9)：728-739

8 秦士洪,倪校军,曹桓铭等.蒸压粉煤灰砖砌体应力-应变全曲线研究.建筑结构学报,2010,31(8)：94-100

9 刘桂秋.砌体结构基本受力性能的研究.[博士论文].湖南：湖南大学,2005

10 杨伟军,施楚贤.砌体受压本构关系研究成果的述评.四川建筑科学研究,1999,27(3)：52-55

11 Robotnov YN.Creep rupture. The 12th International Congress on Application Mechanics,Stanford,1968

12 GB20010-2010混凝土结构设计规范.北京：中国建筑工业出版社,2011

13 Naraine K,Sinha S.Behavior of brick masonry under cyclic compressive loading.Journal of Structural Engineering, 1989,115(6)：1432-1445

14 Naraine K,Sinha S.Cyclic behaviour of masonry in biaxial compression.Journal of Structural Engineering,1991, 117(5)：1336-1355

15 Oliveira DV.Mechanical characterization of stone and brick masonry. Report 00-Dec/E-4,Universidade do Minho, Departamento de Engenharia Civil,Guimar˜aes,Portugal, 2000

(责任编辑：刘希国)

UNIAXIAL COMPRESSION ELASTIC-PLASTIC DAMAGE MODEL WITH DOUBLE PARAMETERS OF BRICK MASONRY1)

NIU Lijun2)ZHANG Wenfang3)
(College of Architecture and Civil Engineering,Taiyuan University of Technology,Taiyuan 030024,China)

This paper presents a damage constitutive model for masonry subjected to axial monotonic and cyclic compressive loading,based on related theories and test results.In order to establish f i ne lever models,double parameters consisting of the peak compressive strain and the strength are adopted to adjust the deformation curve.The uni-axial model presented is consistent with the existing elastic-plastic models,and the mechanical property of masonry materials that a higher strength generally leads to a lower ductility.Assuming that a unloading path of the cyclic constitutive model is linear,a bilinear deterioration function of the unloading compressive stif f ness is established by utilizing two test results,and a linear interpolation of the compressive strength for the degradation rate that is permitted.

masonry,constitutive relationship,damage model,cyclic loading,simulation

TU313.3

A

10.6052/1000-0879-16-207

2016-06-21收到第1稿，2016-08-06收到修改稿.

1)国家自然科学基金(50978177)和山西省科技攻关项目(20110313026-3)资助.

2)牛力军，讲师，硕士，主要从事工程结构抗震研究.E-mail：niulijun@tyut.edu.cn

3)张文芳，教授，博士生导师，主要从事工程结构抗震减震设计理论与应用研究.E-mail：zhangwenfang@tyut.edu.cn

牛力军,张文芳.砖砌体双参数单轴受压弹塑性损伤力学模型.力学与实践,2017,39(1)：35-39

Niu Lijun,Zhang Wenfang.Uniaxial compression elastic-plastic damage model with double parameters of brick masonry.Mechanics in Engineering,2017,39(1)：35-39