基于改进遗传-单纯形混合算法的危险气体泄漏溯源分析*
何 宁,徐 波,孙恩吉
(1.公安部消防局,北京 100054;2.中国安全生产科学研究院,北京 100012)
0 引言
当发生危险气体泄漏事故后,首先需要了解泄漏点的位置及泄漏源强,这是制定应急方案的基础和依据之一。通常情况下,由于应急人员自身安全、地形、时间等限制因素,无法直接确定泄漏位置、测量泄漏源强,只能对有限的几个点位进行监测,因此,往往需要推算出可能的泄漏位置和泄漏源强。目前,有关气体泄漏反算的方法和模型,大致有2种思路:一种是基于概率统计学方法,利用大气扩散的数值分布规律,运用不同的算法进行统计分析,从而反演出泄漏源的位置或源强;另一种是基于优化理论方法,即构造合适的目标函数,计算目标函数的最优化解[1]。概率统计学方法方面,殷凤兰[2]在已知点源个数及其位置的前提下,应用最佳摄动量正则化算法对源强进行数值反演;文献[3]采用模式搜索法对气体泄漏源进行定位,而贝叶斯推理法则用于反算泄漏源参数;刘斌[4]发现,SO2浓度与其紫外光谱差分吸收度的综合统计量之间存在联系,可用一系列综合统计量对SO2浓度进行非线性标定。这类算法通常要依据经验对模型参数先行假设,需要大量的观测数据,并在此基础上进行统计分析和数值反演,不符合应急场合快速测量和定位的需求。优化理论方法,其关键在于构造目标函数,再利用遗传算法、单纯形算法、模式搜索算法、人工神经网络算法等不同方法,求解目标函数的最优解。在气体溯源方面,大部分学者选用气体浓度的理论计算值和实际观测值的对应关系作为目标函数,如骆蓓[5]、史阳[6]、吕袭蒙[7]等。在求解目标函数最优解方面,较多采用单纯型法[5-6]和遗传算法[7];张建文[8]则同时使用了遗传算法和单纯形法,即混合遗传-单纯形算法模型,既避免了遗传算法的“早熟问题”,又解决了单纯形法对初始值比较敏感的弊端,但计算速度慢;张久凤[9]则混合了单纯形法和粒子群算法;郑小平[10]利用模式搜索算法迭代优化,也得到一定的应用。遗传算法收敛速度较慢,单纯形法对初始值比较敏感,对于不同的初值单纯形法可能导致发散,或者产生混沌[11]。通过对遗传算法的选择算子进行改进,采用模拟旋转滚花轮(roulette)的算法,同时采取“优质基因保留”策略,可提高遗传算法的计算速度,称为改进遗传算法。本文即是针对以上算法方面的不足,将改进遗传算法和单纯形法结合起来,形成一种混合算法IGA-NM(Improved Genetic Algorithm -NelderMead),该算法既能快速收敛,又对初始值不敏感,能够解决遗传算法的早熟问题,更适用于应急响应场合的应用。
1 IGA-NM混合算法
1.1 改进遗传算法(IGA)
假设先期测量的n个点位的气体浓度监测值为FC(i),其中i=1,2,…,n;另外假设模型中还有M个未识别的点位浓度,则可定义目标函数如下:
(1)
式中:FL(i)为点位i的气体浓度理论值。
假设给定计算精度ε,则式(1)的最优解条件应满足:
φ≤ε
(2)
具体计算时,需要先对遗传算法种群进行初始化,并设定种群的随机取值范围、杂交率、变异率、种群大小、种群迭代次数等。
使用适应度来对个体进行评价,适应度定义如下:
(3)
式(3)中,T为一可调节常数;φ为指数的系数,取正数。
适应度高的个体有选择、杂交、变异3种操作。在操作之前,需要把每个个体进行二进制编码,每个个体即为1个二进制串,串中的每个编码即为1个基因。选择、杂交、变异操作完成之后,再把二进制编码还原。

“优质基因保留”策略则是,在选择过程中,尽可能保留适应度大的个体,剔除适应度小的个体。具体做法如下:
1)以每次迭代后适应度最大的个体,替代适应度最小的个体;
2)父代中适应度最大的个体,直接复制到下一代中,不参与杂交和变异。
杂交是选择2个二进制串,设定杂交概率Pc∈[0,1],随机变量ξ∈[0,1],若ξ>Pc,则这2个二进制串进行交叉操作,即相互交换部分基因(二进制编码)。交叉位置也是随机的。
生态园内北坑塘水面面积约为9 416 m2,南坑塘水面面积约为8 396m2,两处坑塘深度约2.5~3 m,容积约为3万m3,可收集区域内一年一遇最大24小时降雨(43 mm)径流 1.9万 m3。设计坑塘边坡不做硬性坡面防护工程,使用草皮及水生植物绿化护坡,边坡比为1∶3,部分动水位冲刷区采用鹅卵石码放,稳固岸坡。坑塘及周边可绿化面积约7 348 m2,坑塘常水位以下岸边浅水区种植菖蒲、水葱、千屈菜等水生植物,水体中种植荷花。坑塘周边设置花园广场,广场内设下凹式绿地、渗滤草沟等生态措施。
变异是选择1个二进制串,设定变异概率Pm∈[0,1],针对该串中的每个基因产生随机变量ξ∈[0,1],若ξ 经过杂交和变异的二进制串,将加入一个新的种群,直到满足式(3)要求,或超过设定的进化代数。 遗传算法在实现过程中,可能存在早熟现象。早熟即所求得的解为局部最优解,而不是全局最优解。单纯形法,可增强算法的全局搜索能力,以避免早熟。单纯形法有4种基本操作:反射(reflection)、扩展(expasion)、压缩(contraction)和收缩(shrink)。 假设以下特征点:最好点:best;次差点:soso;最差点:worst;反射点:r;扩展点:e;内压缩点:c1(center和worst之间);外压缩点:c2(center和r之间)。 单纯形法按照以下规则操作: 1)如果反射点值小于best,那么考虑扩展点e,选r和e中小者去替换worst。 2)如果反射点值小于soso,用r如替换worst。 3)非以上2种情况,考虑压缩点:①worst比r小,那么考虑c1,如果c1比worst小,选c1替换,否则考虑收缩;②r比worst小,那么考虑c2,如果c2比r小,选c2替换,否则考虑收缩。 当混合算法判断出现早熟时,可从种群(含有N个个体)中随机抽取M+1个个体(M为待优化的参数个数,M+1 应用IGA-NM混合算法,设计一套基于GIS的计算气体泄漏源强和位置的程序。程序采用Eclipse作为集成开发环境,使用Maven进行Java项目管理,用户只需在程序界面中设置大气稳定度(A,B,C,D,E,F)、风速(单位m/s)、地形(平原、郊区、城区)、已泄漏时间(单位s)等几个简单参数,并获取3个以上点位的监测浓度值(可直接在WebGIS上点选输入),即可反算气体泄漏位置和源强,并且在WebGIS上闪烁显示泄漏源位置。 由于遗传算法是一种近似优化算法,其每个解都是近似最优,因此每次计算结果可能都有细微差异。在实际应用场景中,对于同一工况条件,可重复计算多次,取其平均值。 为测试模型及程序的可靠性及适用性,在某化工园区进行了2次实验测试。实验1以某SO2排气口为泄漏点,稳定泄漏排放1 000 s后,在其下风向设置8个监测点;实验2以某废气排放口为泄漏点,稳定泄漏排放160 s后,在其下风向设置5个监测点。2次实验的工况条件如表1所示。 表1 实验工况条件Table 1 Experimental condition 实验1各监测点位置及测量浓度如表2所示。 表2 实验1各监测点位浓度Table 2 Monitoring site concentration of experiment I 实验2各监测点位置及测量浓度如表3所示。 表3 实验2各监测点位浓度Table 3 Monitoring site concentration of experiment II 图1 实验1溯源结果在地图上的展示Fig.1 Traceability results of experiment I 图2 实验2溯源结果在地图上的展示Fig.2 Traceability results of experiment II 反演源强计算10次取其平均值如表4。 表4 源强反演计算结果Table 4 Calculation results of source strength inversion 反演泄漏源位置与实际泄漏源位置的误差距离,实验1平均为9.6 m,实验2平均为7.8 m,该误差对于气体泄漏溯源场景在可接受范围内。 按照实验1的工况条件,分别采用GA(种群数量200)、GA(种群数量1 600)、NM(源强初值假设为0)、NM(源强初值假设为9 996)、IGA-NM混合算法(种群数量1 600)5种方法,各计算10次后取其平均值,结果对比如表5所示。 表5 GA、NM和IGA-NM混合算法的计算比较Table 5 Comparison of GA, NM and IGA-NMhybrid algorithms 对比结果表明,IGA-NM混合算法计算速度较快,且位置误差和源强误差最小。 1)描述了一种结合改进遗传算法和单纯形法的IGA-NM混合算法,该算法既避免了GA的收敛过慢,又避免了NM初值敏感,兼顾了全局优化。与GA、NM相比,IGA-NM混合算法的计算速度更快,计算误差更小。 2)基于IGA-NM设计了危险气体泄漏溯源应用程序,用户只需要在程序界面中设置少数几个简单参数,在地图上点选监测点位、输入监测浓度值,即可反算气体泄漏位置和源强,并且在WebGIS上闪烁显示泄漏源位置。该程序简化了输入参数,使用更加方便快捷,可适用于危险气体泄漏应急监测、大气污染源溯源反查等场景。 [1]张建文,刘茜,魏利军.危险化学品泄漏事故泄漏源强反算方法比较研究[J].中国安全科学学报,2009,19(2):165-171. ZHANG Jianwen, LIU Qian, WEI Lijun. Comparative Study on the Back-calculation Methods for the Intensity of Leakage Sources in Chemical Leakage Accidents[J]. China Safety Science Journal, 2009, 19(2):165-171. [2]殷凤兰,李功胜,贾现正.一个多点源扩散方程的源强识别反问题[J].山东理工大学学报(自然科学版),2011,25(2):1-5. YIN Fenglan, LI Gongsheng , JIA Xianzheng. An inverse problem of determining magnitudes of multi-point sources in the diffusion equation[J]. Journal of Shandong University of Technology (Natural Science Edition), 2011,25(2):1-5. [3]陈增强.危险化学品泄漏源的定位研究[D].北京:北京化工大学,2013. [4]刘斌, 孙长库, 张弛,等. 基于统计量的差分吸收光谱烟气SO2浓度反算方法[J]. 光谱学与光谱分析, 2011, 31(1):197-200. LIU Bin, SUN Changku, ZHANG Chi,et al. Concentration retrieving method of SO2using differential optical absorption spectros copy based on statistics [J]. Spectros copy and Spectral Analysis, 2011,31(1):197-200. [5]骆蓓.基于MATLAB的液化气体源强反算研究[D].哈尔滨:哈尔滨理工大学,2015. [6]邹吉然.非重气泄漏事故源强反算研究[D].哈尔滨:哈尔滨理工大学,2014. [7]史阳. 有毒气体罐车运输泄漏的源强及位置反算研究[D]. 兰州:兰州交通大学, 2013. [8]吕袭蒙. 基于CPU的源强反算算法研究[D].大连:大连理工大学,2011. [9]张建文,王煜薇,郑小平,等.基于混合遗传-Nelder Mead单纯形算法的源强及位置反算[J].系统工程理论与实践,2011,31(8):1581-1587. ZHANG Jianwen, WANG Yuwei, ZHENG Xiaoping, et al. Back-calculation of source strength and position by a hybrid genetic-Nelder Mead simplex algorithm [J]. Systems Engineering-Theory & Practice, 2011,31(8):1581-1587. [10]张久凤. 基于监测数据的源强反算算法研究及应用[D].北京:中国石油大学, 2011. [11]郑小平,陈增强.模式搜索算法在毒气泄漏中的源强反算[J].中国安全科学学报,2010,20(5):29-34. ZHENG Xiaoping, CHEN Zengqiang. Back calculation of source strength and location of toxic gases releasing based on pattern search method[J]. China Safety Science Journal, 2010,20(5):29-34. [12]韩炜,廖振鹏.一种全局优化算法:遗传算法-单纯形法[J].地震工程与工程振动,2001,21(2):6-12. HAN Wei, LIAO Zhenpeng. A global optimization algorithm: genetic algorithm-simplex [J]. Earthquake Engineering and Engineering Vibration, 2001, 21(2):6-12. [13]王海清,王玉秀,宋贤生,等.采用遗传算法优化气体探测器布局策略研究[J].中国安全生产科学技术,2016,12(9):86-91. WANG Haiqing, WANG Yuxiu, SONG Xiansheng, et al. Study on layout optimization strategy of gas detectors using genetic algorithm [J]. Journal of Safety Science and Technology, 2016,12(9):86-91. [14]王登科,王洪磊,魏建平.颗粒煤的多扩散系数瓦斯解吸模型及扩散参数反演研究[J].中国安全生产科学技术,2016,12(7):10-15. WANG Dengke,WANG Honglei,WEI Jianping.Multi-diffusion coefficient model and diffusion parameter inversion of gas desorption for coal particles [J]. Journal of Safety Science and Technology, 2016,12(7):10-15. [15]曾令杰,高军.基于遗传算法的空调风系统突发污染快速溯源[J].同济大学学报(自然科学版),2017(8): 1198-1203,1208. ZENG Lingjie, GAO Jun. Genetic algorithm for sudden contaminant source identification in ventilation system[J]. Journal of Tongji University (Natural Science), 2017(8):1198-1203,1208.1.2 单纯形法(NM)
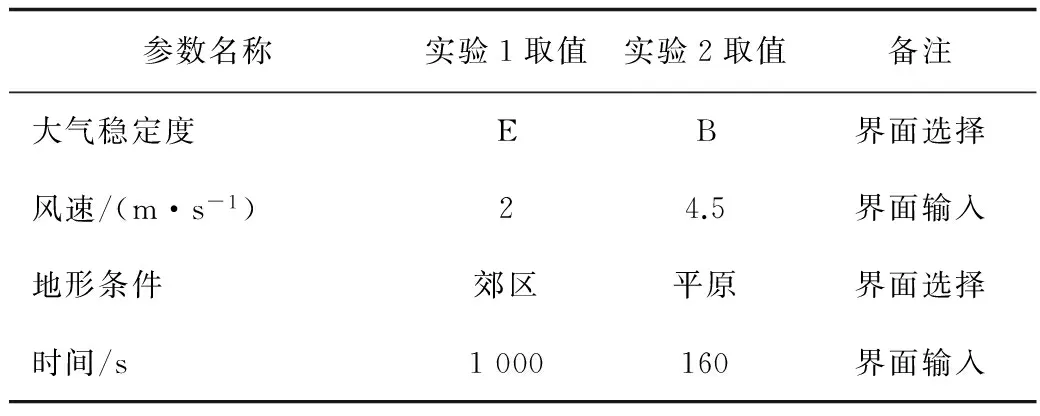
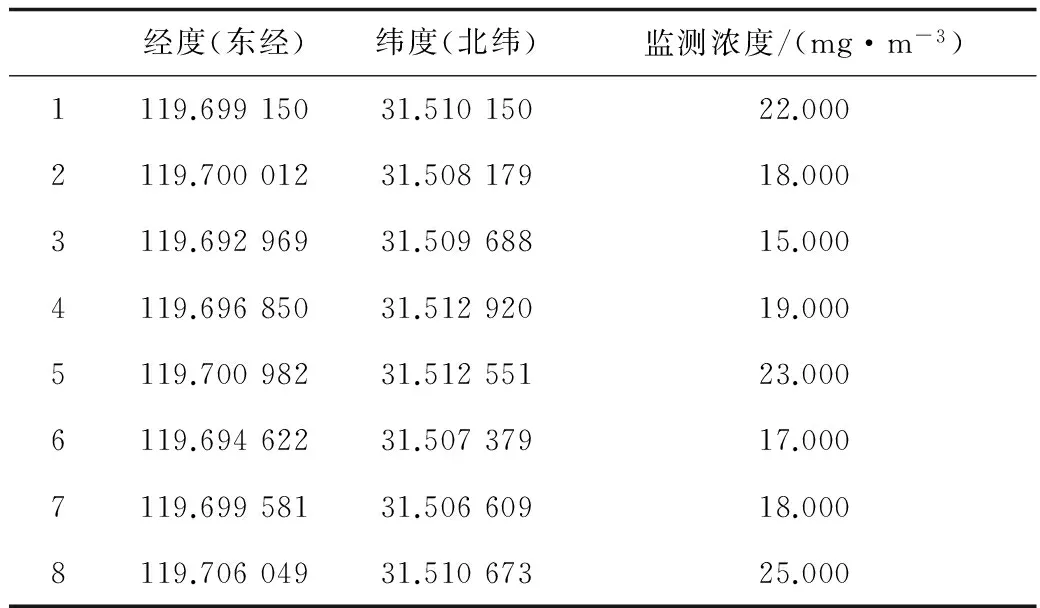
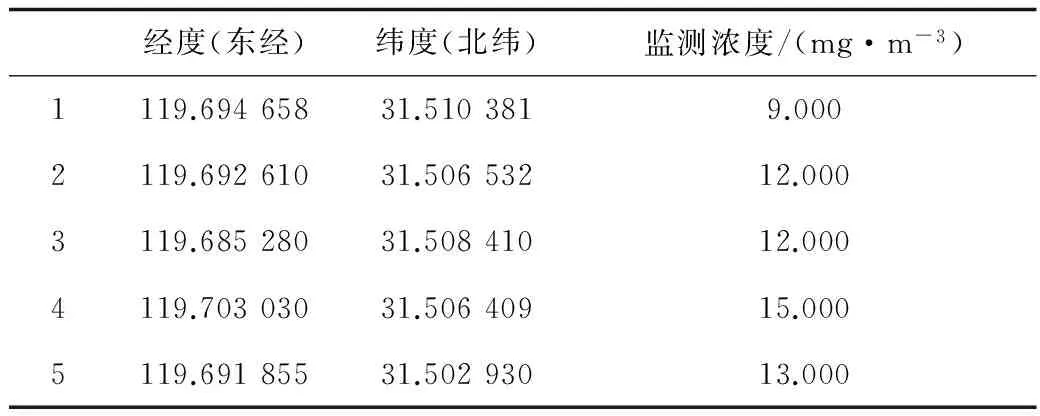
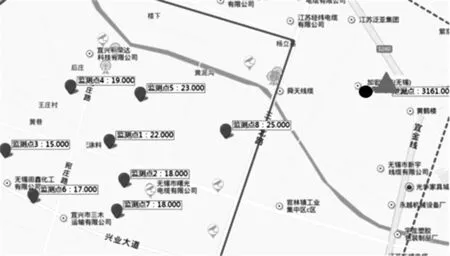
2 应用示例与讨论




3 结论

