铀尾矿库WSN安全监控镜像约束域定位算法*

余修武，范飞生，夏　凡，周利兴，刘　永，李向阳，张　枫

(1.南华大学 环境与安全工程学院，湖南 衡阳 421001； 2.金属矿山安全与健康国家重点实验室，安徽 马鞍山 243000；3.湖南省铀尾矿库退役治理技术工程技术研究中心，湖南 衡阳 421001)

0　引言

安全监测监控技术一直是制约铀尾矿库安全生产与治理的关键技术之一。铀尾矿库一般范围较大，且其中存在大量的具有放射性污染和有毒有害的物质，现今大多还是处于人工现场采集数据或使用卫星遥感、航拍成像等高危险、高成本的监测监控方式，而无线传感器网络(WSN)因具有适用于各种复杂、恶劣和危险的监测环境且成本低廉等特点，被广泛应用于各种监测领域，为铀尾矿库监测提供了一个全新的技术手段。

定位技术是WSN用于确定信息源位置、监控目标方向的关键技术之一[1-3]，及时获取铀尾矿库突发事件发生区域的位置信息，能够为铀尾矿库的安全预警提供方位。定位是节点对周围环境和目标参数信息的收集及提取，辅以角度、距离、时钟等多维参数进行计算获取自身或其他节点的准确位置[4-5]。定位技术能够对各种复杂、危险环境发生的突发事件进行精确定位及追踪。

RSSI属于典型的定位算法[6-9]，其容易实现、成本低、无需额外硬件且能够方便的从无线芯片的寄存器中直接读取，但由于其在铀尾矿库中会受到非视距、多径等因素的影响，远距离RSSI值测距容易产生较大误差[10-11]，针对RSSI测距误差问题，文献[12]提出了一种正态分布跟踪动态方差模型(LNSM-DV)，并引入最小二乘法动态调整LNSM-DV，分析RSSI方差和距离的关系用来减小RSSI的测距误差；文献[13]提出在物理层中使用片内多径分离技术求取抗干扰RSSI值；文献[14]依据RSSI值大小求取权重并计算质心来增加定位精度；以上这些算法均需获取大量的RSSI值进行分析，因此增加了通信开销，且计算中所涉及的RSSI值，在距离大于某一值时，RSSI波动造成的随机干扰很难进行消除，会使局部误差增大。为此，提出一种未知节点只利用少量近距离RSSI值测距生成最小通信圆，依据镜像原理生成镜像圆的约束域定位算法(Image minimum communication circle constraint region location algorithm,IMC-CC)，该算法可屏蔽远距离RSSI值，减少干扰、降低测距误差。

1　镜像最小通信圆约束域理论

镜像理论[15]最早由法国精神医生拉康提出，他认为人生是从镜子开始认识自我、引导自我和约束自我的一个过程，镜像其实是冗余的一种类型，简单的可以称之为复制版本，其具有功能的同向性和扩展应用无差别性，镜是呈现像的载体，像是自我认识、引导和约束的复制同构体。镜像最小通信圆借鉴于镜像理论，未知节点通过通信范围识别认识自我，即未知节点以自我为圆心生成最小通信圆，并根据已知节点(锚节点)绝对坐标模拟锚节点开始引导自我，即锚节点以自身为圆心生成相同镜像圆，最终由未知节点和锚节点构成了一个镜像圆结构模型，由锚节点镜像圆交叉约束未知节点位置达到定位效果。

1.1　最小通信圆

未知节点(S节点)以一定功率向其周围锚节点发送识别信号，锚节点收到识别信息后反馈自身位置坐标和得到的RSSI值给S节点,如图1有A，B，C和D4个锚节点，S节点收到4个RSSI值，分别为RSSIA，RSSIB，RSSSC和RSSID，S节点对RSSI值进行降序排列，如RSSIB>RSSSC>RSSIA>RSSID，并分别计算到各锚节点的距离，设分别为dA，dB，dC和dD。

定义在S的通信范围内，以S节点自身为圆心，以某锚节点到S节点的间距为半径生成的圆，称为最小通信圆。如图1(a)所示为S节点以dB为半径，自身为圆心生成的最小通信圆，图1(b)为以dC为半径的最小通信圆。在A，B，C和D节点中，B节点离S节点距离最小，生成的最小通信圆也最小。

1.2　交叉镜像圆

同理最小通信半径可以取dA和dD。

2　铀尾矿库节点定位

铀尾矿库一般规模较大，节点呈平面网状结构布设，其结构给节点间通信带来了便利，通信阻碍较少。如图2所示为某铀尾矿库节点的布设示意图，未知节点或新加入节点(如附着与移动机械或人员的移动节点以及节点死亡后新增加的节点)可通过周围已知节点，使用镜像最小通信圆约束域理论，确定自己的位置信息。

图2　铀尾矿库各节点布设示意Fig.2　Uranium tailings node layout schematic diagram

2.1　最小通信圆半径

在RSSI定位算法中，常用的对数路径损耗模型[16]如式(1)所示。

RSSI=A-10nlgl

(1)

式中：A表示信号经过1 m传输路径后的路径损耗值；l为信号传播距离；n表示传播因子，和具体无线传播环境有关。

n值在不同环境中变化很大，需对其进行修正。在S节点的通信范围内，存在多个锚节点，可以认为在此通信范围内传播因子n相同。若在S节点的通信范围内，存在多个锚节点互相通信(在保证一定节点密度情况下)，锚节点相互之间以相同功率发送信号，收集RSSI值并发送至S节点。另外，由于无线信号传播受到非视距、多径传播等因素的影响，远距离的RSSI值测距误差较大，为避免较远距离测距所产生的误差较大，只取其中几个最大RSSI值作为修正参数，如B和C，D节点之间为2个最大RSSI值，则建立修正模型如式(2)所示。

(2)

式中：RSSIBC为B节点接受到来自C节点的RSSI值，同理RSSIBD；lBC表示B和C节点间距可通过节点坐标求得，为已知值，同理lBD。

由式(2)可得：n=(RSSIBC-RSSIBD)/ [10lg(lBD/lBC)]，

则未知节点最小通信圆半径可通过式(3)求得，以dB为例。

(3)

2.2　定位区域优化

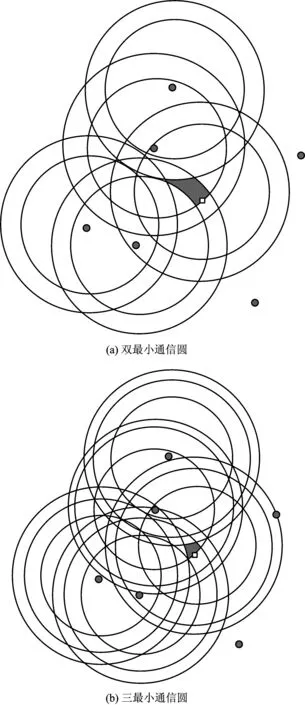
图3　多半径最小通信圆镜像交叠Fig.3　Image overlap of multi-minimum communication circles

从图1可以看出，最小通信圆的半径不同，所得到的定位区域范围具有差异性。同时，锚节点的分布排列也是影响定位范围的重要因素。由于节点分布的不确定性，约束区域也会呈现多样性，单一半径的最小通信圆不能很好的约束节点存在范围，在此可通过2个或2个以上半径的最小通信圆镜像交叠处理，如图3(a)为以dB和dC为半径的最小通信圆镜像交叠图，约束区域相对于单一半径进一步缩小，约束区域简称为SBC，则SBC=SB∪SC，且SBC≤SB，SBC≤SC；图3(b)为三半径的最小通信圆镜像交叠图。

2.3　最小通信圆误差估算

设网络总面积为M，锚节点均匀分布密度为β，则锚节点的单位覆盖面积m1=1/β，为方便计算，取其面积为正方形，则边长a2=1/β，锚节点形成九宫格图形。

1)若最小通信圆半径为最小RSSI值间距(如上述dB)，有dB≤a,则：

①当dB≤a/2，则镜像圆无交叉区域，未知节点位于B节点镜像圆。

2)若最小通信圆半径如上述dC，有a/2

当β=0.01，即a=10 m时，在理想圆环境下，不同单最小通信圆半径的最大误差如图4所示。

当多个最小通信圆交叠时，存在部分面积不重叠，进一步缩小定位区域，误差将进一步缩小，且小于最小最大误差rmin。

图4　理想圆环境下单最小通信圆最大误差Fig.4　The biggest error under the single minimum communication circle

3　仿真与分析

3.1　算法网络仿真与分析

本文提出的IMC-CC算法由S节点主导、锚节点辅助完成定位，S节点无需获取大量RSSI值进行分析，降低了通信开销，以最小通信半径生成镜像圆，镜像圆交叠约束与反约束生成定位估计区域，以面积迭代运算估计定位，实现了算法的运算低复杂度。

为了分析IMC-CC算法的性能，利用MATLAB建立1个200 m×200 m范围的仿真环境，总节点数为100，所有位置布设节点概率相同但不重复布设，设置不同β，节点最大通信距离为50 m，分别对传统的RSSI、RSSI加权、单一最小通信圆、双最小通信圆和三最小通信圆IMC-CC定位算法进行定位精度误差和误差方差进行实验和分析，其中最小通信圆半径为降序选取RSSI值计算所得。

图5所示为不同算法的未知节点在不同β情况下的平均误差，仿真结果表明：随S节点密度的增加，误差都趋于减小，可以看出单一最小通信圆IMC-CC与传统的RSSI算法平均误差最大且比较接近，双最小通信圆IMC-CC算法和RSSI加权质心算法平均误差较为接近且居中，而三最小通信圆IMC-CC算法平均误差最小。最小通信圆数量的不同表征着约束条件的多少，数量越多约束条件越多。IMC-CC误差主要由2大因素决定，一是选取的计算最小通信圆半径RSSI值，降序选取能够有效减少由外界环境波动产生的误差；二是圆化位置估算产生的误差，多约束条件能够减少限制定位区域面积，降低定位误差。

图6为3种β值下各种算法的单节点误差，单一子图显示5种算法均呈现出和平均误差相同的变化规律，但单节点误差会有波动性变化，传统RSSI和单一最小通信圆IMC-CC波动性比较明显，其它算法波动性相对较弱，单一条件的约束性具有的不确定性相对较大。同时可以看出，已知节点密度的增加，能够有效减小其误差及误差波动(方差)，表1所示为不同β值下5种算法定位误差的标准差，误差标准差是表征算法稳定性的关键指标，从表中可以看出双最小通信圆和三最小通信圆IMC-CC算法标准差较小，其稳定性相对其余3种算法较高。

表1　误差标准差(σ)Table 1　Error standard deviation(σ)

图5　平均误差Fig.5　Average location error value of S nodes

图6　不同β下的单节点误差Fig.6　Signal node error

图7　误差累计占比分布Fig.7　Cumulative proportion of error distribution

3.2　实验评估

无线传感器网络在铀尾矿中的应用研究属于新型研究领域，目前还处于理论与实验相结合的研究阶段。而在实际应用中，节点最大通信距离一般约为60 m至100 m，节点可通过等距离或随机抛洒布设，2节点间布设距离通常约在10 m至30 m，单节点的通信范围内存在多个邻节点，监测点密度完全满足工程应用的需求。

4　结论

1)提出一种适用于大规模平面结构的铀尾矿库安全监测的镜像最小通信圆约束域(IMC-CC)定位算法，其能够较精确地定位节点的位置信息，有利于铀尾矿库的信息监测和安全预警。

2)IMC-CC算法利用少量较大RSSI值测距约束定位，并利用节点通信的相对性，未知节点生成最小通信圆，锚节点镜像最小通信圆形成镜像圆交叉约束域，并且多最小通信圆交叉区域交叠，形成了一种多约束条件的定位，是测距和非测距模型的一次有效结合。

3)通过仿真模拟和实验，在控制已知节点的密度情况下，得出最小通信圆交叠数越多，IMC-CC的定位精度更高，误差标准差呈梯度下降趋势，且多最小通信圆误差能够快速收敛，相对于传统RSSI和RSSI质心算法，多最小通信圆误差及其稳定性都较为优越。

4)在实验中发现，测量的近距离RSSI值的波动不可避免，存在少数未知节点约束域偏离，增加了测量误差，后续研究需进一步修正减少此误差。

[1]Xie Q, Fan X R, He Q, et al. Location Model and Algorithm of Construction Waste Recycling Centers for Service Reliability[J]. Journal of Intelligent Systems, 2014, 24(2):287-297.

[2]Jia K, Meng L I, Tian Shu B I, et al. A voltage resonance-based single-ended online fault location algorithm for DC distribution networks[J]. Science China(Technological Sciences), 2016, 59(5):721-729.

[3]KIM W, PARK J, KIM H J, et al. A multi-class classification approach for target localization in wireless sensor networks[J]. Journal of Mechanical Science and Technology, 2014, 28(1): 323-329.

[4]BABAIE-KAFAKI S, GHANBARI R, MAHDAVI-AMIRI N. Hybridizations of genetic algorithms and neighborhood search metaheuristics for fuzzy bus terminal location problems[J]. Applied Soft Computing, 2016, 46(46): 220-229.

[5]MARIAPUSHPAM I T, RAJAGOPAL S. Improved algorithm for the location of CPG islands in genomic sequences using discrete wavelet transforms[J]. Current Bioinformatics, 2017, 12(1): 57-65.

[6]余修武，周利兴，范飞生，等．基于新内点测试与Grid-SCAN的铀尾矿库监测定位算法[J]．中国安全生产科学技术，2016，12(5)：5-9．

YU Xiuwu,ZHOU Lixing,FAN Feisheng,et al.A localization algorithm for uranium tailings monitoring based on new interior point test and Grid-SCAN[J].Journal of Safety Science and Technology,2016,12(5):5-9.

[7]ZHANG Li-ping, LIM C C, CHEN Yi-ping, et al. Tracking Mobile robot in indoor wireless sensor networks[J]. Mathematical Problems in Engineering, 2014(5): 1-8.

[8]Yiu S, Dashti M, Claussen H, et al. Wireless RSSI fingerprinting localization[J]. Signal Processing, 2016, 131:235-244.

[9]AWANG A, AGARWAL S. Data aggregation using dynamic selection of aggregation points based on RSSI for wireless sensor networks[J]. Wireless Personal Communications, 2015, 80(2): 611-633.

[10]Li X, Chen L, Wang J, et al. A Novel Method to Improve the Accuracy of the RSSI Techniques Based on RSSI-D[J]. Journal of Networks, 2014, 9(12) :3400-3406.

[11]Feng W J, Bi X W, Jiang R. A Novel Adaptive Cooperative Location Algorithm for Wireless Sensor Networks[J]. International Journal of Automation and Computing, 2012, 09(5):539-544.

[12]Xu J, Liu W, Lang F, et al. Distance Measurement Model Based on RSSI in WSN[J]. Wireless Sensor Network, 2010, 2(8):606-611.

[13]罗炬锋，邱云周，付耀先，等．研究片内多径分离技术在基于RSSI定位中的应用[J]．电子与信息学报，2011，33(4)：891-895．

LUO Jufeng,QIU Yunzhou,FU Yaoxian,et al.Research on separation of subchip multipath components for RSSI-bashed location application[J].Journal of Electronics&Information Technology,2011,33(4):891-895.

[14]韩东升，杨维，刘洋，等．煤矿井下基于RSSI的加权质心定位算法[J]．煤炭学报，2013，38(3)：522-528．

HAN Dongsheng,YANG Wei,LIU Yang,et al. A weighted centroid localization algorithm based on received signal strength indicator for underground coal mine[J].Journal of China Coal Society,2013,38(3):522-528.

[15]Caulkins C G. Bridge over troubled discourse: the influence of the Golden Gate Bridge on community discourse and suicide[J]. Journal of Aggression, 2015, 7(1):47-56.

[16]Guo G, Wang N, Zhang K. Distance difference algorithm based on rssi for highway vehicle localization[J]. Sensors & Transducers (1726-5479), 2014,169(4):170-173.