明晰问题本质 探究多种途径

[摘 要] 在高中数学教学中，若能适时渗透多种解法，有助于展现思维发散的独特性，培养学生的创新能力.“多解”不仅是高效题解教学的策略，也为培养创新能力开辟了途径.以一道向量高考试题为例，从多角度进行变式、探究，以期增强学生灵活应用所学知识解决问题的能力.

[关键词] 几何；基底；坐标；一题多解

对于同一道题，从不同的角度去分析，会让我们得到不同的启示，从而引出多种不同的解法. 通过不同视角的观察，使我们的思维拓展到不同的方向、不同的层次，防止思维定式，从而达到举一反三、触类旁通之效. 本文以2016江苏卷第13题的“多种解法”为例说明.

[?] 问题展示

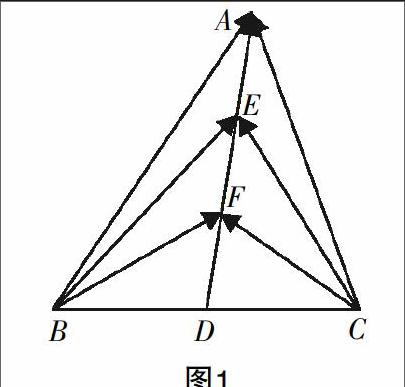
例 （2016年江苏卷第13题）如图1，△ABC中，D是BC的中点，E，F是AD上的两个三等分点. 若·=4，·= -1，则·=_____________.

[A][B][C][E][F][D]

图1

向量在高中数学中起着重要的工作作用，其在平面几何、解析几何、立体几何，甚至其他学科都有着广泛的应用. 高考对平面向量的直接考查通常以平面几何为背景，如三角形、四边形等. 命题形式通常以数量积、平行、垂直、夹角问题为条件或结论. 问题求解的基本策略是结合平面几何的几何性质，利用向量加法的三角形（或平行四边形）法则、减法的三角形法则进行转化，或者利用坐标法将几何问题进行代数化处理.

[?] 多角度探究

1. 几何性质

解法1 如图1，由于·=·=[（+）2-（-）2]=[（2）2-2]=

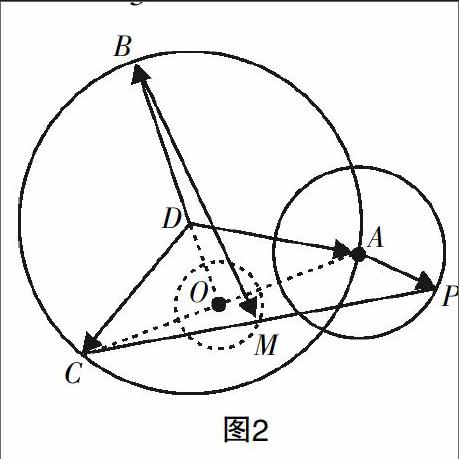
变式1 （2016年四川卷第10题）在平面内，定点A，B，C，D满足

2的最大值是（ ）

=1，=，则点P在以A为圆心、半径为1的☉A上运动，且M为CP的中点，因此根据平面几何中的位似变换可知，点M在以CA的中点O为圆心、半径为=的圆上运动. 由此，

的最大为2的最大值为.

评析：在本题的求解中根据题目已知条件，结合平面几何的性质构造出相应的圆是问题顺利解决的关键.

[?] 选基底

解法2 令=a，=b，则=-b，=2a，=3a，=3a-b，=3a+b，=2a-b，=2a+b，=a-b，=a+b，

则·=9a2-b2，·=a2-b2，·=4a2-b2.

由·=4，·=-1可得9a2-b2=4，a2-b2=-1，因此a2=，b2=，因此·=4a2-b2=-=.

变式2 在△ABC中，点M，N满足=2，=.若=x+y，则x=________ ；y=________.

解析 由=2，=可得=2（-），-=-，即=，=（+），所以=-=（+）-=-，则x=，y=-.

评析：根据平面向量基本定理，通过平面向量的线性运算，将所求向量表示成已知向量的线性组合，进而使问题顺利得解.

[?] 巧建系

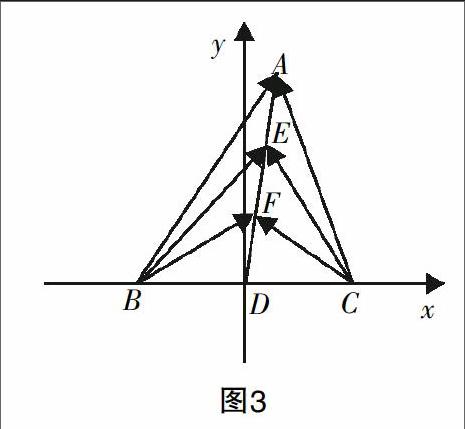
解法3 如图3所示，以点D为坐标原点、BC所在直线为x轴，建立平面直角坐标系.

设A（x，y），BC=2m，则B（-m，0），C（m，0），D（0，0），=（x+m，y），=（x-m，y）. 所以·=x2-m2+y2=4. ①

又E，F是AD上的两个三等分点，所以=，=，所以E

①-②得x2+y2=5.

① -②得m2=，m2=.

代入式③得·=x2-m2+y2=-=.

变式3 △ABC三边BC，CA，AB上的中线分别为AD，BE，CF，记BE∩CF=G，求证：=（+）.

证明：任取一点O作原点，建立平面直角坐标系xOy，记A（x1，y1），B（x2，y2），C（x3，y3），则E

所以=2，B，G′，E三点共线；

同理，可得C，G′，F三点共线，按题意，G'即G，从而，得==

-x1，-y1

=（x2+x3-2x1，y2+y3-2y1），

因为+=（x2-x1，y2-y1）+（x3-x1，y3-y1）=（x2+x3-2x1，y2+y3-2y1），

所以=（+）.

评析：本题求解中以坐标的代数运算实现问题的解答. 先按照目标构造点G′，再证题设中的G即为G′. 实质上证明了三角形重心G的一个特征性质：++=0（已知此式成立，设△ABC的重心为G′，则由已证，得++=0，再把两式相减，得3=0，即=0，故点G为重心.）

[?] 解法评析

一题多解的目的不在于“多”而是启迪思维、开拓思路、提升发散思维的水平，帮助学生融会贯通地运用所学知识分析问题与解决问题.

解法1以向量加、减法的三角形法则为工具，结合向量数量积的定义，利用共点向量的运算法则，实现未知向已知的转化.

解法2基底法作为比坐标法更一般性的方法，有着非常广泛的应用，解题中当我们一时无法得到对问题直观形象的几何解释时，可借助基底法.基底法是平面向量的本质，是解决向量问题的通法，是培养思维能力的有效途径.

解法3着眼于向量的坐标运算，通过建立坐标系、引入点的坐标将几何问题代数化处理.数形结合思想是高中重要数学思想之一，其包括“以形解数”和“以数解形”两个方面，而向量法就是以数解形的有力体现.

从以上解答的分析过程可见多角度探究一道题目的解答过程，体现了不同知识之间的相互沟通. 这种基于问题结构的合理联想并和自身的解题思维联系起来的解题策略，有利于提高學生综合运用已学知识解答数学问题的能力. 教学中教师要锻炼学生在不同的知识背景下用不同的方法解决同一个问题的能力，进而可使学生在解决数学问题上快速做出合理判断，选择最佳解题途径.