探究微命题微方法 培养学生核心素养

[摘 要] 数学核心素养是具有数学基本特征、适应个人终身发展和社会发展需要的人的必备品格与关键能力，是数学课程目标的集中体现，是在数学学习的过程中逐步形成的. 通过理解数学核心素养的六个维度：数学抽象、直观想象、逻辑推理、数学建模、数学运算和数据分析，从数学的微命题和微方法入手，探索数学核心素养的有效培育途径.

[关键词] 数学核心素养；微命题；微方法；向量

数学核心素养是具有数学基本特征、适应个人终身发展和社会发展需要的人的必备品格与关键能力，是数学课程目标的集中体现，是在数学学习的过程中逐步形成的. 数学核心素养是数学课程改革的新指向，已经成为数学教育教学的培养目标. 本文通过理解数学核心素养的六个维度：数学抽象、直观想象、逻辑推理、数学建模、数学运算和数据分析，从数学的微命题和微方法入手，探索数学核心素养的有效培育途径.

[?] 聚焦数学核心素养，构建微命题和微方法理念

随着高中数学有效教学方式的不断改进，研讨微专题成为高中数学的一个热点.目前可以发现很多研究微专题的方式方法，但“只有适合的方法才是最佳的方法”. 我们在教学中，常常会遇到学生对知识点了解不够的窘境，即课本概念和解题需要之间看似“脱节”，这时需要归納总结，提取几个关键命题（本文称作“微命题”），突出几个关键方法（本文称作“微方法”）.

要有效培养学生的数学核心素养，最有效的方法是将传统的专题转变为以能力为主线的微专题，探究数学的微命题和微方法. 以期通过微命题和微方法的探究，提升学生的数学核心素养，让学生学会“用数学的眼光观察世界，用数学的思维分析世界，用数学的语言表达世界”. 本文以向量的几何应用为例，从微命题和微方法入手，谈谈数学核心素养的有效培育途径.

[?] 培养数学核心素养，演绎微命题和微方法探究

研究向量的内涵实质，用向量的观点研究教材的知识结构体系，培养学生学会运用向量解决问题的意识和能力.以向量为工具，实现“数与形”的结合，变抽象的数学逻辑为具体的向量运算，通过向量就能比较容易地解决某些数学问题.

1. 向量表示直线的微方法

用向量表示直线，最先可以看作直线的两点式方程.

设直线上的动点为M，则过两定点A，B的直线l的方程为：

=λ，λ∈R. （1）

设直线外一点O，则由（1）可推得过两定点A，B的直线l的方程为：

=（1-λ）+λ，λ∈R. （2）

我们不妨称（2）为直线的外点式方程，有时（2）可写为

=α+β（α+β=1）. （2′）

上述形式都是由参数确定动点位置的. 设p是直线外一点O到直线l的距离，O点到l的垂直方向所作的单位向量称为单位法向量，则直线l上任意点M满足

·n=p. （3）

这个式子称为直线的法线式方程，它是用垂线表示直线的一种方式，且与坐标无关.在直角坐标系中，设n=（cosθ，sinθ），θ是法线与x轴的夹角，M（x，y），则xcosθ+ysinθ-p=0.法线式方程在坐标平面上表示夹角和距离时非常有用，例如，设直线外一点N（x0，y0）到直线l：Ax+By+C=0的距离是d，则l的法向量为n= ±

又如，设直线l1：·n1=p1，l2：·n2=p2，则两直线夹角就是它们法向量的夹角，其余弦值为cosθ=

n1·n2

，当直线表示为一般式时，即A1x+B1y+C1=0，A2x+B2y+C2=0，就有cosθ=.

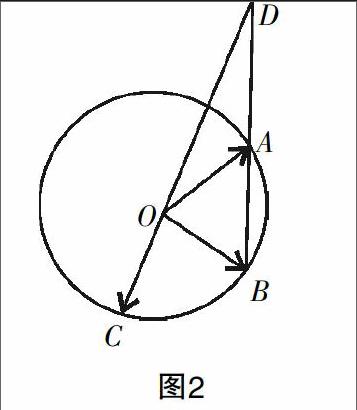
例1：如图3，A，B，C是圆O上的三点，CO的延长与线段BA的延长线交于圆O外一点D，若=m+n，则m+n的取值范围是________.

变式：已知点G是△ABO的重心，若PQ经过点G，且=a，=b，=ma，=nb，求证：+=3.

课堂简录：通过小组交流讨论，学生围绕向量表示直线的微方法，可以比较轻松地解决此类问题.

学生1：对于例1，设=λ+（1-λ）·，设=u，则u<-1，于是==+，m+n=+=∈（-1，0）.

学生2：变式中，因为点G是重心，=a+b，于是

因为P，Q，G三点共线，所以=，从而+=3.

师：此类问题的思维含量较高，但不管怎样，只要建立向量表示直线的三个数学模型，复杂问题都能轻松的简单化.

设计意图：从学生知识的“最近发展区”出发，探究向量表示直线的微方法. 在探求用向量表示直线的三种微方法及其证明、应用过程中，让学生体会、感受数学概念和数学结论的形成过程：观察、猜想、归纳、证明、抽象和概括. 在教师的指引下，探索用数学的思维分析问题、发现问题、提出问题，动手实践、亲身体验等探究性活动，感悟数学逻辑，数学抽象等素养，发展学生数学思维能力，提升数学核心素养.

[?] 向量表达式的微命题

设，是平面上两个不共线的非零向量，则平面上任何向量都可以表示为=α+β的形式，并且

（1）当α+β=1时，A，B，M三点在同一条直线上，当α+β>1时，点M与点O在直线AB的异侧，当α+β<1时，点M与点O在直线AB的同侧.

（2）上述表示式是唯一的，即若另有=m+n，则m=α，n=β. 证明如下：

（1）若α+β>1，设α+β=λ>1，则+=1，=+，在直线AB上，故点M与点O在直线AB的异侧；同理，若α+β<1，则点M与点O在直线AB的同侧.

（2）由=m+n知（α-m）= -（β-n），但，不共线，故m=α，n=β.

问题：当α+β≠1时，α+β能否对应更精确的几何位置呢？不妨再以α+β>1为例分析.设=α+β，α+β=λ>1，则点M与点O在直线AB的异侧. 设OM的连线与直线AB相交于点N，则==（α+β），故（α+β）=1，即=α+β=λ.

课堂简录：各小组通过合作探讨，展示研究成果，总结解决此问题的策略，其余小组对其进行补充完善，教师最后总结点评.

师（总结点评）：上式表明，α+β的值是线段OM与相应截线段ON之比. 这个结论非常重要：点M离AB越“远”，α+β的值越大. 用类似的方法可以划定α+β的取值与点M位置所在区域的对应，如图5.

有了这段分析，上面例1的结果一目了然，而例1的变式也可以更快地得到解决：因为P，Q，G三点共线，存在α，β（α+β=1）使得=α+β，即

a+b=αma+βnb，得=αm，=βn，故1=α+β=+.

例2：已知△OAB，其中=a，=b，M，N分别为三角形OA，OB边上的点，满足=a，=b，设AN与BM相交于点P，则=_______.

变式：给定两个长度为1的平面向量，，它们的夹角为120°，（1）点C在以O为圆心的圆弧AB上变动，若=x+y，求x+y的最大值；（2）当∠BOC=30°时，求x+y的值.

课堂简录：通过小组合作讨论，展示研究成果并总结解决问题的策略，教师总结点评.

生3：例2，令=λ+（1-λ）=λa+b，

同样地令=μ+（1-μ）=a+（1-μ）b，

則λ

=，

=1-μ，由此解得λ=，μ=，因此=a+b.

师：不错，对微命题的运用很到位，确立了问题模型的思考辨析能力，将问题的难度一下就降低了.

对于变式，也能容易解决，（1）x+y是两线段之比，故当OC⊥OD时取得最大比值2.（2）∠BOC=30°时，OD=，x+y==.

设计意图：通过观察、分析，构建数学模型，从特殊到一般，抽象归纳出数学的一般规律，形成数学命题并推广到更一般的情形，并将数学模型用准确的数学语言、数学符号表达出来.把握数学内容的本质，提升学生直观想象、数学建模等核心素养.

[?] 向量坐标表示的微命题

设有点O（0，0）和点A（x，y），将向量绕点O逆时针旋转θ角至，问A′（x′，y′）的坐标如何表示？这个问题有两种方法处理，一是放到极坐标系中，令A（rcosθ1，rsinθ1），则A′（x′，y′）=（rcos（θ1+θ），rsin（θ1+θ））=（rcosθ1cosθ-rsinθ1sinθ，rsinθ1cosθ+rcosθ1sinθ）=（xcosθ-ysinθ，xsinθ+ycosθ）.

另一方法是转化为复数，即对应的复数为x+yi，则对应的复数就为（x+yi）·（cosθ+isinθ）=（xcosθ-ysinθ）+i（xsinθ+ycosθ），从而x′=xcosθ-ysinθ，

y′=xsinθ+ycosθ.

特别地，如果旋转角θ=90°，则x′= -y，y′=x. 比起坐标系变换公式的推导，这两个方法都很简洁，应用时很方便.

例3：已知点A为直线l：x+2y-4=0上任意一点，点C（2，4），以AC为直角边作Rt△ABC，其中AB=AC（A，B，C按顺时针排列），求·的最小值.

解：设A点坐标为（x，y），则=（2-x，4-y），因是向量绕点A逆时针旋转θ=90°所得，所以=（-4+y，2-x），从而=+=（x，y）+（-4+y，2-x）=（-4+x+y，2-x+y），·=（x，y）·（-4+x+y，2-x+y）=-4x+2y+x2+y2=（x-2）2+（y+1）2-5.

上式的最小值是以C（2，-1）为圆心的一簇圆的半径的平方减5的最小值，当然在圆与直线l相切时取得这个最小值，C（2，-1）到直线l的距离为d=，所以

-5即为所求.

例4： 设a，b为正数，xOy平面内两点A（a，0），B（0，b）是正三角形ABC的两个顶点，C在第一象限，若△ABC含于点集D={（x，y

0≤x≤1，0≤y≤1）}中，求点（a，b）所在平面区域的面积.

课堂简录：通过小组合作探讨，各小组展示研究成果，最后教师进行总结点评.

师（总结点评）：△ABC含于区域D内，当且仅当是点C含在D内，当且仅当向量绕点A顺时针旋转60°后所得后的C点含在D内. 而=（-a，b），故的复数形式为-a+bi，得的复数形式为

问题转化为：D′={（a，b）

0≤a≤1，0≤b≤1}内求区域0≤+b≤1，0≤+a≤1所围的面积，不难求得该面积为6-3.

[A][B][E][O][x][D][C][y]

图9

设计意图：在整个教学过程中，要树立发展学生的数学核心素养为导向的教学意识，将核心素养的培养贯穿教学活动的始终.在教学过程中要训练学生打破思维定式，要敢于求新求异，训练学生多层次、多角度、多方向的思维活动，增加学生思维的厚重度.

对解题方法和命题的归纳和应用，是数学素养的基本体现，有的教师主张启发学生从自主探究中获得结果. 但是若对功底不太雄厚的学生，这个要求不太现实，这时需要教师挖掘题目中的内在结构和功能，找出方法上的共同关联，以帮助学生轻松解题.

本着“以生为本”的理念，突出学生主体地位，站在学生的角度，阐明通过数学抽象过程生成数学抽象素养，依靠数学理性思维生成数学逻辑推理素养，凭借数学综合实践生成数学建模素养，研究数学问题解决生成直观想象素养，依赖数学算法算理生成数学运算素养，借助数学统计思维生成数据分析素养. 总之，在课堂教学中，要树立以发展学生数学核心素养为导向的数学教学意识，探究数学微命题和微方法，有效培养学生数学核心素养.