计及厚度下量子点量子比特的电磁场依赖性
乌云其木格, 尹洪武, 苏 都, 额尔敦朝鲁*
(1. 内蒙古民族大学 物理与电子信息学院, 内蒙古 通辽 028043;2. 河北科技师范学院 物理系, 河北 秦皇岛 066004; 3. 中国石油大学 化学工程学院, 北京 102249)
计及厚度下量子点量子比特的电磁场依赖性
乌云其木格1, 尹洪武2, 苏 都3, 额尔敦朝鲁2*
(1. 内蒙古民族大学 物理与电子信息学院, 内蒙古 通辽 028043;2. 河北科技师范学院 物理系, 河北 秦皇岛 066004; 3. 中国石油大学 化学工程学院, 北京 102249)

量子点的厚度; 极化子; 量子比特; 电磁场依赖性
1 引 言
近年来, 人们提出了多种实现量子计算机的方案[1-5], 其中量子点量子比特方案由于其可以集成的优点成为最有可能的方案。因此,许多学者对量子点中的二能级体系进行了研究[6-9],取得了一批重要成果。由于大多数的人工纳米结构是由极性半导体材料制备的,所以极化效应强烈地影响着它们的物理性质,而且维度的降低,必将导致更强的电声子相互作用,使得极化子效应更加明显和有趣,因而,国内外有不少学者研究了极化子效应对量子点量子比特的影响[10-13]。然而,人们对电子-声子相互作用对量子点量子比特的影响的研究大多都把量子点当作二维圆形结构来处理。事实上,近年来实验上已能制备出几个分子层厚度的量子点[14]。因此,如果把量子点描写为柱形或薄盘形结构应更为准确[15-17]。显而易见,当计及量子点厚度时,必将导致被约束在量子点中的电子-声子相互作用体系基态和激发态的变化。面对量子点存在厚度的客观事实,研究量子点厚度对量子点量子比特性质的影响是一个有实际意义的基本问题。
本文采用Lee-Low-Pines-Pekar型变分法推导出计及量子点厚度下量子点中强耦合极化子的基态和第一激发态能量本征值和本征函数以及平均声子数的电磁场依赖性,在此基础上,以磁极化子的二能级结构为载体构造了量子点量子比特。通过数值计算揭示了量子点厚度、LO声子效应及电磁效应等对量子点量子比特的概率分布、振荡周期、消相干等性质的影响,为探索调控量子点量子比特的有效物理方法提供根据。
2 模型与计算
设电子处于厚度为L的无限高势垒量子点(亦即量子盘,Quantum disks,QDs)中。建立直角坐标系,Oz轴在盘的中心轴线上,x-y平面与盘中心轴线垂直并通过盘的中点,如图1所示。设外加电场F沿x轴方向,外加磁场B沿z轴方向,矢势用A=B(-y,x,0)/2描写。电子-LO声子耦合体系的哈密顿量为[10,12]
H=He+HF+Hph+He-ph,
(1)

图1 量子盘的示意图
式中,右边第一项表示电子的动能。由于电子在z方向的限制比x-y方向的限制大得多,因此,在z方向仅有最低的电子导带被占据,则z方向与x-y平面没有耦合[18-19],那么上述3D问题就可以分解为x-y平面内的2D问题和z方向的1D问题来处理。He就可以表示为
(2)
选取x-y平面和z方向量子盘的限定势V(ρ)和V(z)分别为
(3)

HF=-e*Fx,
(4)
是电子在电场中的势能;式(1)中第三项和第四项

(5)
(6)

(7)
其中,v、α、ε和ε0意义与文献[13]相同,rp为极化子的半径。
(8)
这里
(9)

表示声子的真空态,由
(12)
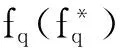
fq(λ0)=
(13)
再经过冗长的计算,得到基态和第一激发态极化子平均声子数分别为
(15)
(16)
极化子的基态能量和第一激发态能量分别为

(17)
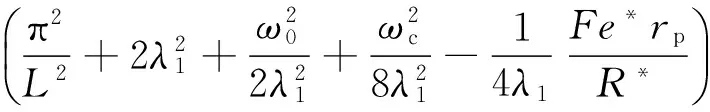
(18)
其中R*=ћωLO为LO声子能量常数。至此,可以构造一个二能级体系,当电子处于叠加态
Ψ(ρ,z,t)=
(19)

(20)

(21)
在低温条件下,引入色散关系ω=ωLO-ηcq2,基于费米黄金规则和偶极近似,声子的自发辐射率为[13]:
(22)
其中ε0为介电系数,c为光速,η为色散系数,ΔE=E1-E0为基态和第一激发态之间的能基础,τ为消相干时间。
3 结果与讨论
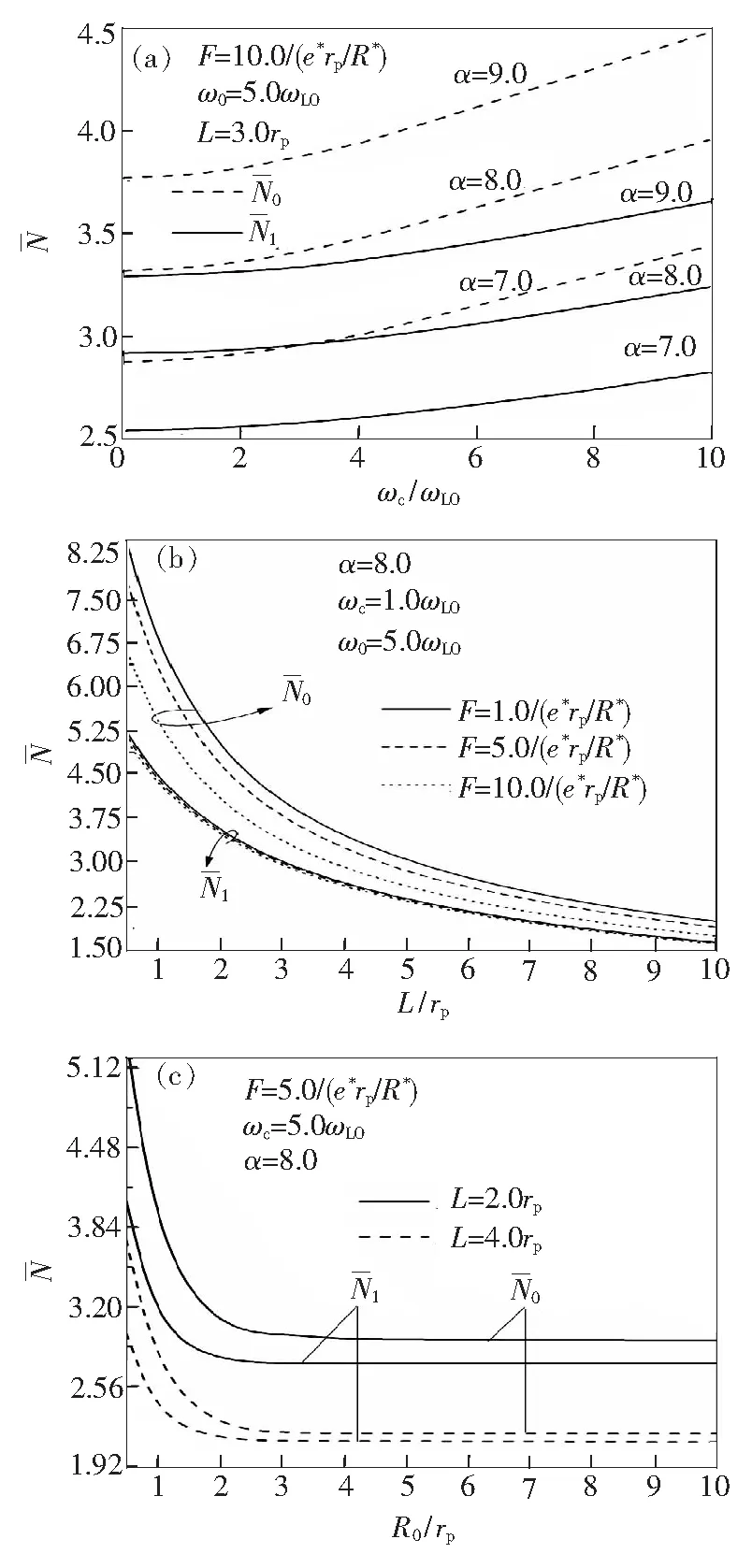



图3 极化子的基态能量E0和第一激发态能量E1在不同α下随ωc的变化(a)、不同F下随L的变化(b)以及不同L下随R0的变化(c)。
Fig.3 Ground state energyE0and the first excited state energyE1as a function of the cyclotron frequencyωc at different coupling strengthα(a), the thicknessLof the QDs at different electric fieldsF(b), and the transverse effective radiusR0at different thicknessLof the QDs(c), respectively.
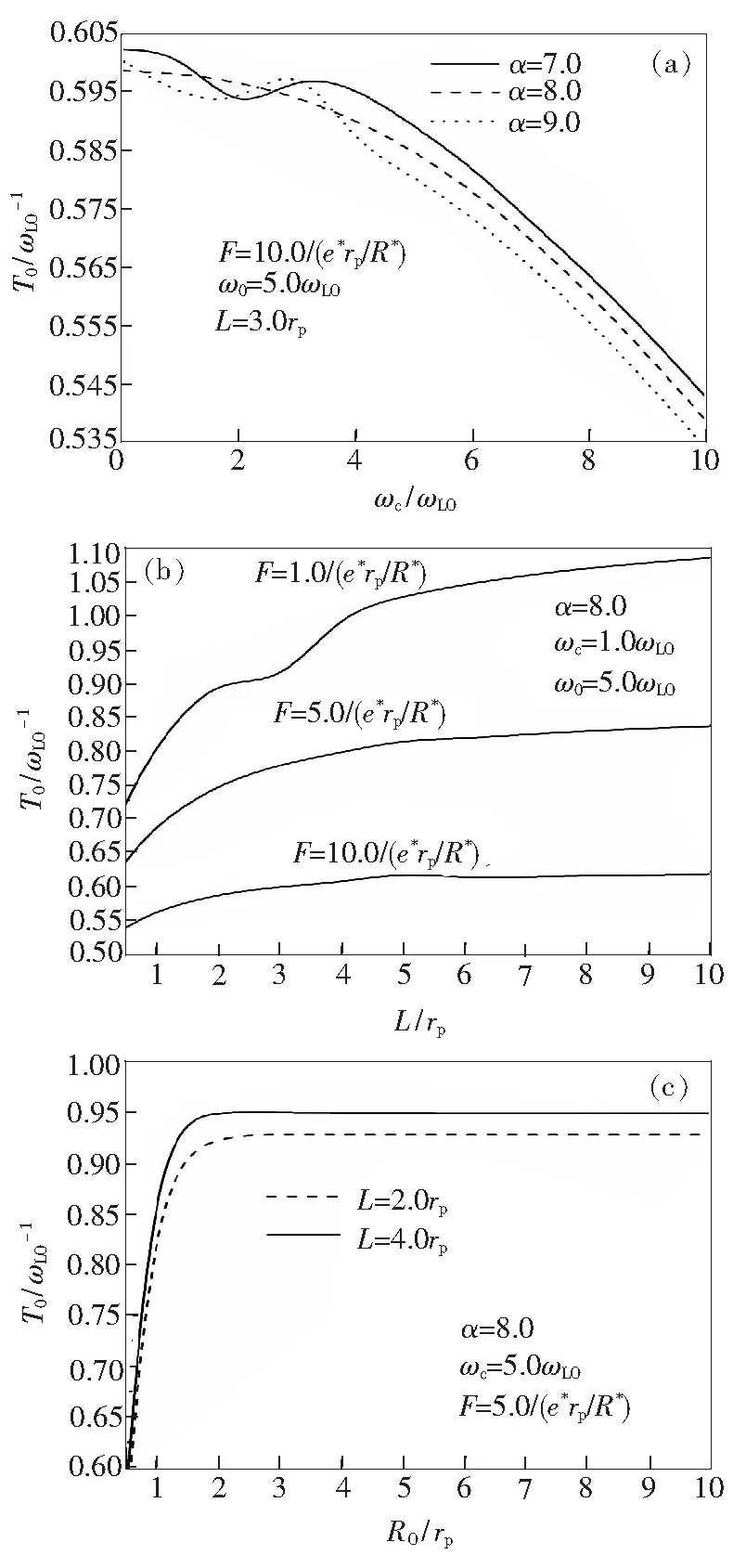
图4 量子比特的振荡周期T0在不同α下随ωc的变化(a)、在不同F下随L的变化(b)以及在不同L下随R0的变化(c)。
Fig.4 Oscillation periodT0of the qubit as a function of the cyclotron frequencyωcat different coupling strengthα(a), the thicknessLof the QDs at different electric fieldsF(b), and the effective radiusR0at different thicknessLof the QDs(c), respectively.
图4表示了振荡周期T0在不同α下随ωc的变化、在不同F下随L的变化以及在不同L下随R0的变化。由图4(a)可以看出,对不同的α而言,T0随ωc的增加而振荡减小或单调下降。这与文献[10]的结论定性一致;当ωc较小时,T0随α增加而出现振荡,当ωc较大时,T0随α增加而减小,这与文献[21]的结论一致。由式(21)和图3可推断,这些是ωc或α对能级差ΔE的影响所致。由图4(b)可以看出,T0随L的增加而小幅振荡上升。当L一定时,T0随F的增加而减小,这与文献[22]的结论一致。由图4(c)可以看出,T0随R0增加而增大并呈“型”曲线。这些特性表明,我们可以通过设计不同厚度的量子点并结合施加不同强度的电磁场,达成调控量子比特振荡周期大小的目的。
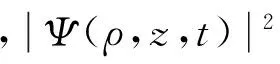



图6 消相干时间τ在不同α和η下随ωc的变化(a)、在不同F下随L的变化(b)以及在不同L下随R0的变化(c)。
Fig.6 Decoherence timeτas a function of the cyclotron frequencyωcat different coupling strengthαand different coefficient of dispersionη(a), the thicknessLof the QDs at different electric fieldsF(b), and the effective radiusR0at different thicknessLof the QDs (c), respectively.
图6表示消相干时间τ在不同α和不同η下随ωc的变化、在不同F下随L的变化以及在不同L下随R0的变化。由图6(a)可以看出,τ随ωc的增加而增大。当ωc一定时,τ随η的增加而增大;当ωc和τ一定时,τ随α的增加而增大。由图6(b)可以看出,当L较小(L<2.0rp)时,τ随L的增加而显著减小;当L较大(L>2.0rp)时,τ随L的增加而缓慢减小。另外,当L一定时,τ随F的增加而减小。由图6(c)可以看出,τ随R0的增加而减小并呈现出“L型”曲线,拐点发生在R0≈2.5rp处。另外,当R0一定时,τ随L的增加而减小。消相干时间τ的上述特性,提供了利用量子盘的厚度结合调节外加电磁场的强度,实现调控量子比特消相干的方法和依据。
4 结 论

[1] CIRAC J I, ZOLLER P. Quantum computations with cold trapped ions [J].Phys.Rev.Lett., 1995, 74(20):4091-4094.
[2] GERSHENFELD N A, CHUANG I L. Bulk spin-resonance quantum computation [J].Science, 1997, 275(5298):350-356.
[3] KANE B E. A silicon-based nuclear spin quantum computer [J].Nature, 1998, 393(6681):133-137.
[4] LOSS D, DIVINCENZO D P. Quantum computation with quantum dots [J].Phys.Rev. A, 1998, 57(1):120-126.
[5] 邬云文, 邓艳, 周小清, 等. 基于两节点间信息互传的量子特性 [J]. 光子学报, 2016, 45(3):0327001. WU Y W, DENG Y, ZHOU X Q,etal.. Quantum properties of information each other between two nods [J].ActaPhoton.Sinica, 2016, 45(3):0327001.(in Chinese)
[6] KYRIAKIDIS J, PENNEY S J. Coherent rotations of a single spin-based qubit in a single quantum dot at fixed Zeeman energy [J].Phys.Rev. B, 2005, 71(12):125332-1-5.
[7] FURUTA S, BARNES C H W, DORAN C J L. Single-qubit gates and measurements in the surface acoustic wave quantum computer [J].Phys.Rev. B, 2004, 70(20):205320.
[8] LI S S, LONG G L, BAI F S,etal.. Quantum computing [J].Proc.Natl.Acad.Sci.U.S.A., 2001, 98(21):11847-11850.
[9] LI S S, XIA J B, LIU J L,etal.. InAs/GaAs single-electron quantum dot qubit [J].J.Appl.Phys., 2001, 90(12):6151-6155.
[10] CHEN Y J, XIAO J L. The temperature effects on the parabolic quantum dot qubit in the electric field [J].J.LowTemper.Phys., 2013, 170(1-2):60-67.
[11] SUN Y, DING Z H, XIAO J L. Effects of magnetic field on the coherence time of a parabolic quantum dot qubit [J].J.LowTemper.Phys., 2014, 177(3-4):151-156.
[12] FOTUE A J, KENFACK S C, TIOTSOP M,etal.. Temperature, impurity and electromagnetic field effects on the transition of a two-level system in a triangular potential [J].Eur.Phys.J.Plus, 2016, 131(4):75-1-7.
[13] XIAO W, XIAO J L. Effects of temperature and electric field on the coherence time of a RbCl parabolic quantum dot qubit [J].Int.J.Theor.Phys., 2016, 55(6):2936-2941.
[14] MEDEIROS-RIBEIRO G, LEONARD D, PETROFF P M. Electron and hole energy levels in InAs self-assembled quantum dots [J].Appl.Phys.Lett., 1995, 66(14):1767-1769.
[15] KASH K, SCHERER A, WORLOCK J M,etal.. Optical spectroscopy of ultrasmall structures etched from quantum wells [J].Appl.Phys.Lett., 1986, 49(16):1043-1049.
[16] REED M A, RANDALL J N, AGGARWAL R J,etal.. Observation of discrete electronic states in a zero-dimensional semiconductor nanostructure [J].Phys.Rev.Lett., 1988, 60(6):535-537.
[17] CHEN C Y, LI W S, TENG X Y,etal. Polaron in a quantum disk [J].Phys. B:Condens.Matter, 1998, 245(1):92-102.
[18] PEETERS F M, SCHWEIGERT V A. Two-electron quantum disks [J].Phys.Rev. B, 1996, 53(3):1468-1474.
[19] PRICE R, ZHU X J, SARMA S D,etal.. Laughlin-liquid-Wigner-solid transition at high density in wide quantum wells[J].Phys.Rev. B, 1995, 51(3):2017-2020.
[20] LEE T D, LOW F E, PINES D. The motion of slow electrons in a polar crystal [J].Phys.Rev., 1953, 90(2): 297-302.
[21] YILDIRIM T, ERCELEBI A. The grounds-state description of the optical polaron versus the effective dimensionality in quantum-well-type systems [J].J.Phys.Condens.Matter, 1991, 3(10):1271-1277.
[22] SUN Y, DING Z H, XIAO J L. The effect of magnetic field on a quantum rod qubit [J].J.LowTemp.Phys., 2012, 166(5-6):268-278.

乌云其木格(1964-),女,内蒙古科左后旗人,教授,2005年于内蒙古民族大学获得硕士学位,主要从事凝聚态光学性质方面的研究。

E-mail: wuyun66@126.com额尔敦朝鲁(1960-),男,内蒙古奈曼旗人,教授,硕士生导师,1982年于内蒙古民族大学获得学士学位,主要从事凝聚态光学性质方面的研究。
E-mail: eerdunchaolu@163.com

Light Conference 2017国际会议通知
一年一度的光学国际学术大会Light Conference将于2017年7月16日至18日在长春召开。此次盛会由中国科学院长春光学精密机械与物理研究所和University of Rochester, USA(美国罗切斯特大学)联合主办,Light: Science & Applications编辑部承办,科技部曹健林研究员、University of Rochester郭春雷教授、基金委秦玉文教授、UCLA Aydogan Ozcan教授担任大会共主席。
一、会议内容
此次会议主题涵盖:地基大口径光学工程、光学超精密加工与检测技术、空间光学工程、飞秒激光与物质相互作用和先进光子学、激光与纳米光子学、生物光子学、绿色光电材料和器件、先进超材料和超表面、低维光电子材料和器件、X射线技术、激光先进制造、微纳光学等。
会议诚邀国内外高校和科研院所相关领域的专家、学者参加,交流、共同分享展示自己的最新研究成果。大会还特设优秀墙报奖,以鼓励学生参会交流。组委会也诚邀国内外公司(企业)参展,为公司近距离接触国内外知名光学专家、展示公司仪器设备提供良好平台。
二、会议投稿
会议论文将择优发表在Light: Science & Applications,Photonics Sensors,《光学精密工程》,《中国光学》,《发光学报》,《液晶与显示》,《红外与毫米波学报》等期刊上,未能在上述正刊上发表的论文将会择优发表在《光学精密工程》增刊上。投稿详情请关注会议官方网站,会议投稿截止日期2017年5月1日。
三、会议费用

注册类别普通注册费学生注册费提前注册(6月16日前)2000元1500元现场注册(7月16号报到)2500元1800元
四、会议地点与联系方式

会议地点:中科院长春光机所(长春市东南湖大路3888号)
住宿地点:长春国际会展中心
联系人:李耀彪;电话:0431-86176851
会议邮箱:lightconference@ciomp.ac.cn
会议网站:http://light-conference.csp.escience.cn(请扫描二维码了解详细会议信息)
注:会议期间食宿自理,无伙食补贴!

此次系列会议由长春文岱会议展览服务有限公司协办,会议费由该公司收取并开具发票。
《Light: Science & Applications》编辑部
2017年3月1日
Electromagnetic Field Dependence of Quantum Dot Qubit with The Thickness of Quantum Dot
WUYUNQIMUGE1, YIN Hong-wu2, SU Du3, EERDUNCHAOLU2*
(1.CollegeofPhysicsandElectronicInformation,InnerMongoliaUniversityforNationalities,Tongliao028043,China;2.DepartmentofPhysics,HebeiNormalUniversityofScience&Technology,Qinhuangdao066004,China; 3.CollegeofChemicalScienceandEngineering,ChinaUniversityofPetroleum-Beijing,Beijing102249,China)*CorrespondingAuthor,E-mail:eerdunchaolu@163.com

thickness of the quantum dot; polaron; qubit; electromagnetic-field dependence
2016-11-08;
2016-12-15
河北省自然科学基金(E2013407119); 半导体超晶格国家重点实验室开放研究基金(CHJG200701); 河北科技师范学院科学研究基金(1301-2506)资助项目 Supported by Natural Science Foundation of Hebei Province (E2013407119); Open Research Foundation of State Key Laboratory of Semiconductor Superlattice (CHJG200701); Scientific research foundation of Hebei Normal University of Science and Technology(1301-2506)
1000-7032(2017)04-0552-08
O469
A
10.3788/fgxb20173804.0552

