“节外”未必“生枝”——两角和与差的余弦的教学掠影及反思

江苏省句容市实验高中 刘洪志

“节外”未必“生枝”
——两角和与差的余弦的教学掠影及反思

江苏省句容市实验高中 刘洪志

《三角恒等变换》是苏教版普通高中课程标准试验教科书必修4中的一章，是前面所学任意角三角函数、诱导公式的延伸和发展，是培养学生推理能力和运算能力的重要素材。“两角和与差的余弦”是本章的起始内容，是后续学习两角和与差的正弦、正切以及二倍角公式的知识基础和方法源泉。由于向量还没有学习，所以在教学过程中要引导学生采用单位圆，利用两点间的距离公式推导两角差的余弦公式，由于教学的对象是三星级普通高中的学生，有一定的逻辑思维能力，对用一般到特殊、数形结合、化归与转化、方程思想已经有了一定基础，但远远未达到综合运用这些方法自主探究和证明两角和与差余弦公式的水平，因此在课的设计上先利用几何法得出公式，再利用单位圆进行严格证明。

下面是笔者本节教学中的部分实录，藉此阐明课堂教学中尊重学生的发现，体现学生学习的主体性。

一、新课引入部分

师：我校正在进行校园安全检查安装工程，工人师傅加固学校的空调外机，发现他们把墙上的小支架（如图1）焊接改造成大支架（如图2）,为了增加稳定性，再增加一个焊点，使立柱CE⊥AD。

已知：在Rt△ABD中，∠ABC=90°，∠AEC=90°，∠DAB=α,∠CAB=β,AC=1，求AE的长。

图1

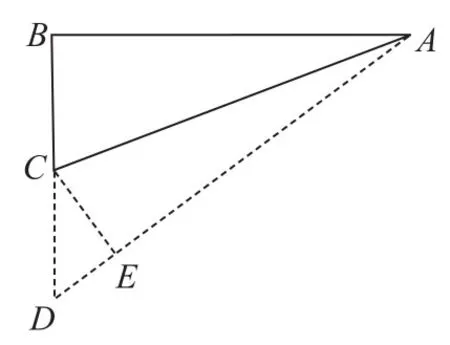
图2

师：大家思考能不能用α，β的三角函数表示？（学生通过小组讨论，有同学展示讨论结果）

生2：AE=AD-DE，分别在两个直角三角形：△ABD，△CDE中来解决问题。

投影学生的解法如下：

师：根据“算两次”的思想方法，两个式子都表示AE，所以有：

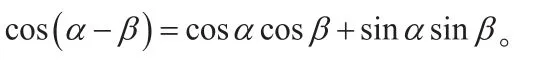
思考：鲁宾斯基曾经说过：“对于形成任何一种能力，都必须首先引起对某种类型活动的十分强烈的需要。”教学中要多些出自身边的问题、学生感兴趣的问题，使他们倍感亲切，跃跃欲试，尤其是解直角三角形问题，学生可以有很大的思考和活动的空间，为一般化证明奠定了目标基础。

二、公式证明部分

师：同学们已经有了处理任意角三角函数问题的，体验了诱导公式的证明，我们是利用了什么图形解决的？

生（全体）：利用单位圆。

师：要证明这个等式对任意角都成立，如果找不到其他办法，不妨就回到我们熟悉的单位圆中来解决问题。

师：请同学们根据下面问题进行小组交流：

问题1：如何在单位圆中做出角α，β，α-β的终边呢？

问题2：角α，β，α-β的终边与单位圆交点P1，P2，P3的坐标是什么？

问题3：如何将角α，β，α-β的终边与单位圆的交点P1，P2，P3的坐标与联系起来？怎样建立这种等量关系呢？

独白：现行的教学理念很崇尚学生探究，实际教学当中如果放手学生自主探究，很多时候会变成漫无目的的探索，常常是无疾而终，在数学教学当中要提升教学的有效性，应该注重数学教学的四个原则：即数学化的原则，适度形式化的原则，问题驱动化原则和渗透数学思想方法的原则。在此环节的处理上采用了“活动单”的方式，布置学生进行小组合作探究，逐步展开，降低公式推导理解难度，进而解决问题，并请同学展示自己的研究成果。先与学生共同确定要探究的内容和目标，明确探究的方法再让学生进行探究，排除更多的无关因素的干扰，力求学生把更多精力放在公式的寻找和证明当中。

（学生经过8分钟左右的讨论，有一个小组发表了自己的研讨结果）

生1：我是这样作图的（如图3所示）：

由三角函数的定义得到：

我发现点P1，P2，P3的坐标有公式中的三角函数，我想要把坐标联系起来。

图3

由两点间的距离公式得：

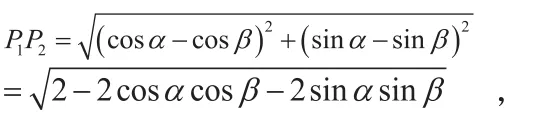
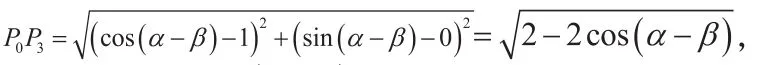
（这位学生数学成绩很好，平常肯钻研，讲解非常清楚，全体同学也都表示了充分肯定。就在课程将要继续时，又有一位同学举手示意，我们称为学生2，学生2数学成绩一般，但是很刻苦，为了鼓励学生积极思考，我示意他回答。）

学生2：老师，我的作图和学生1类似，我也是找两条线段相等，我找的是P0P2=P1P3。

列出式子: