变坡面浅埋偏压隧道松动围岩压力计算方法

刘　翔，房　倩

(北京交通大学 隧道与地下工程教育部工程研究中心，北京　100044)

隧道开挖后，围岩作用于隧道支护结构上的荷载称之为围岩压力。目前计算浅埋隧道围岩压力较为成熟的计算公式主要有全土柱理论、太沙基理论、比尔鲍曼公式和谢家烋公式4种。全土柱理论适用于隧道上覆土层埋深较浅的情况，认为围岩压力直接为土柱全重，因此计算得到的围岩压力偏大。太沙基理论[1]视土体为松散土体，综合考虑了地面荷载、土体黏聚力、埋深和洞室尺寸对围岩压力的影响，但却只考虑土体黏聚力产生的剪切作用，未考虑切向摩擦力和法向力(即土体的夹持力)，并且侧压力系数取的是经验值，因此难以得到准确的围岩压力。比尔鲍曼公式[2]考虑了两侧土体的夹持作用，将滑动面视为直线，假定围岩压力与埋深有关，得到的计算结果与太沙基理论的计算结果一致。谢家烋公式[3]考虑了两侧土体对拱顶土体的夹持作用，是唯一考虑了地形偏压条件的浅埋隧道拱顶隧道围岩压力计算方法，被认为符合工程实际，现行《铁路隧道设计规范》[4]便采用此公式(简称为规范法)。近年来，国内外学者[5-10]还通过上限定理对隧道围岩压力进行了相关研究，然而其计算过程相对较为复杂。此外，国内外学者通过模型试验[11]、数值分析[12-14]及理论分析[15-18]等手段对浅埋偏压隧道围岩的破坏模式以及松动围岩压力的计算方法进行改进。但这些方法都是假设地面为一条水平或倾斜的直线，即地面坡度唯一；然而在实际工程中，很多隧道位于变坡面不规则地形条件下，采用平均坡度对变坡面隧道进行简化处理会使计算结果存在一定的误差，并且这些方法也没有考虑变坡面导致的偏压对围岩水平侧压力的影响。

因此，本文根据极限平衡法，研究变坡面条件下浅埋偏压隧道松动围岩压力的计算方法，以及地表坡度变化对水平侧压力系数的影响。以贵广高速铁路贺街隧道洞口变坡面浅埋偏压段为例，采用给出的计算方法计算其松动围岩压力，并结合现场监测数据，验证该计算方法的合理性和有效性。

1　计算模型

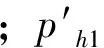
图1　计算模型

2　计算公式推导

2.1　棱体横截面面积的计算公式

取隧道深埋侧(右侧)棱体横截面AC1Cn进行分析，如图2所示。图2中：C1，C2，C3，…，Ci，…，Cn为C1Cn段的变坡点；α1，α2，…，αi，…，αn依次为变坡面与水平面的夹角；δ1，δ2，…，δi依次为变坡面两端点与隧道底A点连线的夹角，并且当选取的截面位于深埋侧时，其值为正值；当位于浅埋侧时，其值为负值。

图2　右侧棱体截面

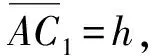
(1)

(2)

右侧棱体截面的面积SL为

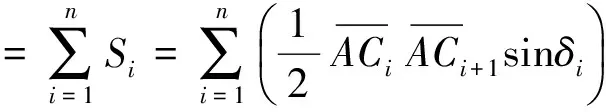
(3)

2.2　推力的计算公式

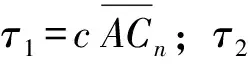
图3　右侧棱体的受力图和力矢量多边形图

根据受力示意图可知

W1=γSL

(4)

式中：γ是土体的容重。

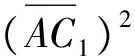
(5)

令αi和δi的函数为K，即

(6)

则式(6)可改写为

(7)

根据力的矢量多边形图，由正弦定理可得

(8)

整理式(8)可得

(9)

根据极限平衡法有

W1+Q+qd+ch=y1+y2

(10)

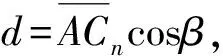
(11)

根据力的矢量多边形图，由正弦定理可得

(12)

将式(7)、式(9)、式(11)代入式(12)并整理可得

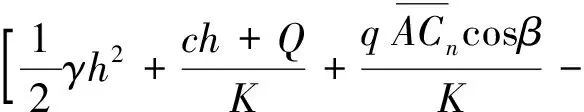
(13)

其中，

(14)

式中：λ为深埋侧水平侧压力系数。

根据普氏理论，可以假设破裂角β=45°+φ/2。根据式(13)可以分别求出在变坡面浅埋偏压隧道深、浅埋侧所提供的推力T和T′，进而可以求得浅埋偏压隧道的松动围岩压力。

因为在自然条件下，可以不考虑集中荷载和均布荷载，以及当黏聚力不存在时，即Q=0，q=0，c=0，则式(13)可简化为

(15)

同理，浅埋侧的推力T′和水平侧压力系数λ′的计算公式与深埋侧的相同，只是浅埋侧变坡处角度用负值表示，因为浅埋侧的坡面情况与计算模型形式相反。

2.3　隧道围岩压力的计算公式

拱顶上覆土层的重度W为

W=γST

(16)

式中：ST为通过拱顶上方不同角度的梯形面积累加得到，即图1中BGC1E的面积。

拱顶垂直土压力p为

p=W+cH+Q+qd-

(17)

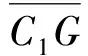
同样，在自然条件下，不考虑集中荷载和均布荷载，以及当黏聚力不存在时，即Q=0，q=0，c=0，则式(17)可简化为

(18)

深埋侧的水平侧压力为

(19)

(20)

当q=0时，将式(15)代入式(19)或式(20)并整理可得

phj=rhjλj=1, 2

(21)

式中：phj为从隧道拱顶到隧道底部任意一点的水平侧压力。

2.4　与规范法的对比分析

当深埋侧地面线为一条倾斜的直线，即不考虑地面为变坡面时，α1=α2=α3=…=αn，则式(6)可简化为

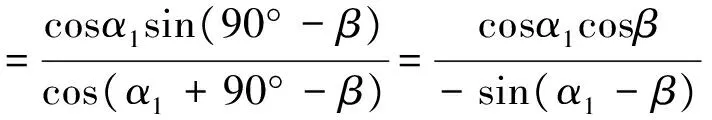
(22)

可见，此时所推导的侧压力系数λ计算公式(简称为本文公式)与规范法的公式相同，说明当本文的计算条件简化为与规范法的计算条件一致时，本文公式可退化为规范法的公式，因此，本文公式更具有普遍性。

与规范法的计算公式对比可知，本文推导的侧压力系数相当于进行了修正，即在规范法的侧压力系数基础上乘以了修正系数K，而K是深埋侧各段变坡角αi和各段变坡点至隧道底部角度δi的函数，所以本文公式的优点在于考虑到了地面坡度的变化，达到了真实的水平。事实上，当深(浅)埋侧地面坡度变化时，必然引起深(浅)埋侧棱体重度的变化，产生的推力则将发生变化，水平侧压力系数必然也随之发生改变。因此本方法比规范法更能真实地反映实际情况。

3　λ影响参数的分析

采用控制变量的方法分析式(6)、式(13)、式(14)、式(18)和式(21)可知：当K值增大时，λ增大，进而两侧土体对拱顶上覆土层的推力增大，拱顶垂直土压力减小，水平侧压力增大；反之亦然。由式(6)可知，影响K值的参数有α和δ，所以分析参数α和δ对λ的影响。选取深埋侧只有2个不同坡面的情况，即只有α1，α2和δ1，δ2的情况进行计算分析。

取摩擦角φ=26°，夹持力摩擦角θ=16°，破裂角β=45°+φc/2，则δ2+δ1=90°-β=32°；α1和α2分别取1，2，3，…，30°；δ1分别取1，2，3，…，32°。根据式(13)计算的侧压力系数λ与各坡度变化关系如图4所示。由图4可知：当α2=15°时，随着α1的增大，K和λ均逐渐增大，最大增大约0.06；当α1=15°时，随着α2的增大，K和λ也逐渐增大，最大增大约0.2；随着δ1的增加(δ1+δ2必为定值)λ的变化曲线为非线性曲线，且随着变坡角α1或α2的降低，λ呈下降趋势。

采用规范法进行计算：同样的基本条件，只是取α1=25°，α2=15°，则计算得到λ=0.61，即图4中α1=20°曲线中的最后1个值，在图4(c)中用箭头直线已标注出来。在相同条件下采用本文推导的计算公式计算，结果为图4(c)中α1=25°的曲线。可以看出：2条曲线距离最大相差0.05，即最大相差的值大约是λ值的1/10～1/12。

由分析可知：随着变坡面角度的增加，水平侧压力系数增大，则由式(15)、式(21)可以看出，随着土体对拱顶上覆土层的推力增大，水平侧压力也增大。由于推力增大，所以拱顶垂直土压力减小，分析结果与工程实际情况相符。并且侧压力系数的变化曲线为非线性的，当变坡面角度相差较大时，本文计算结果与规范法的结果相差较大，说明规范法在变坡面情况下明显不适用。

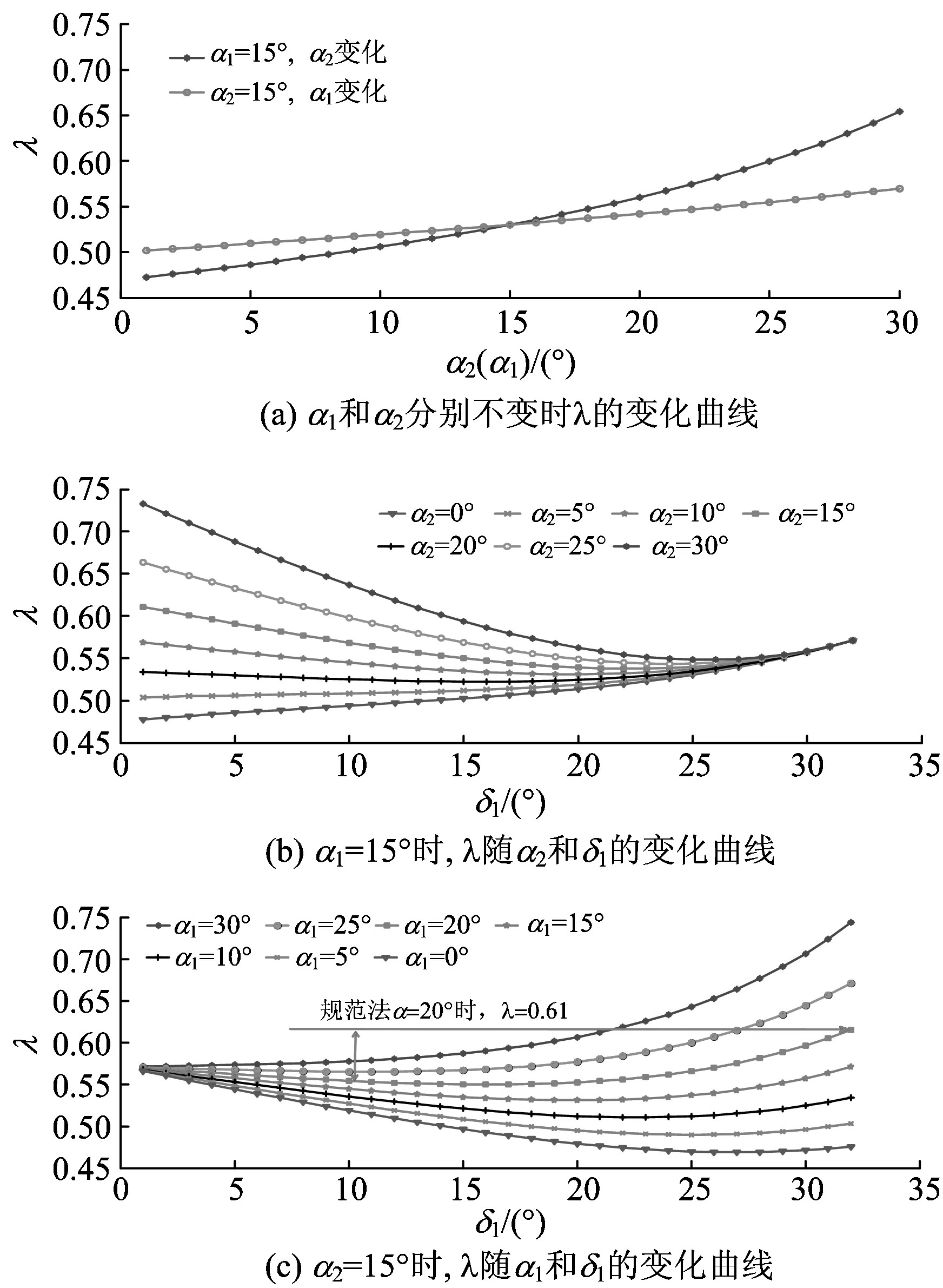
图4　侧压力系数随不同坡度参数的变化曲线

4　案例分析

4.1　工程概况

依托贵广高铁贺街隧道项目验证本文推导公式的有效性和合理性。贺街隧道位于广西壮族自治区贺州市贺街镇境内，为特大断面铁路隧道，全长2 438 m，隧道里程为DK592+58—DK954+496。选取试验段里程为DK592+90—DK592+240，此段为隧道的进口傍山段，存在明显的偏压现象。隧道的埋深为2～20 m，开挖跨度为14.7 m，隧道高度为12.5 m，开挖面积为150 m2。隧道监测段主要为全风化泥质砂岩、粉砂岩夹炭质页岩。其物理力学指标：天然密度为1 980 kg·m-3，含水量为22.51%，弹性模量为43.2 MPa，泊松比为0.33，黏聚力为24 kPa，内摩擦角为16.14°。

共选取该隧道6个断面进行监测，其中第2监测断面的地面坡度变化较大，因此选取第2监测断面作为研究对象，其里程为DK592+155。在施工过程中，第2监测断面初支围岩压力的变化规律如图5所示，稳定后第2监测断面初支围岩压力的分布如图6所示。

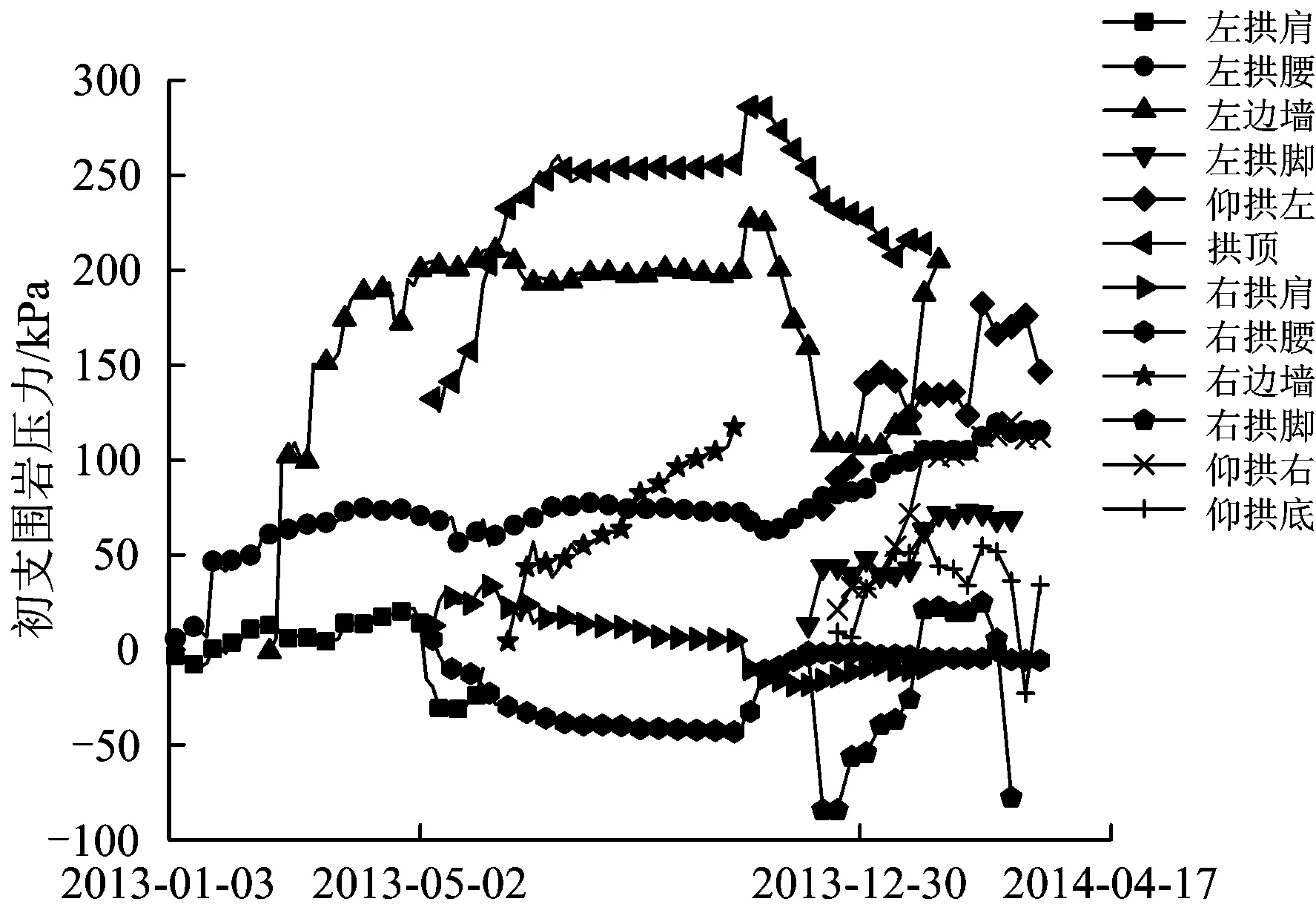
图5　施工过程中初支围岩压力变化情况

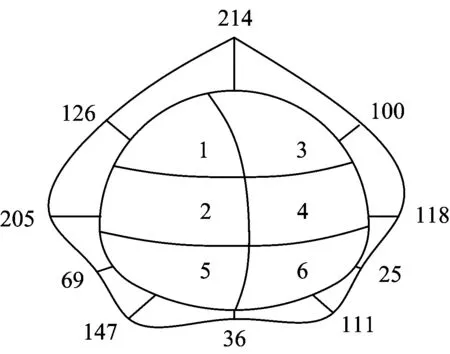
图6　稳定后初支围岩压力(单位：kPa)

4.2　围岩压力

第2监测断面的横断面如图7所示。图7中：B=14.7 m，h=12.97 m，h′=10.35 m，φc=arctan(tanφ+c/σ)=25.94°；α11=6，α12=25；δ11=15，δ12=22；α21=-9，α22=-25；δ21=11，

图7　第2监测断面横断面

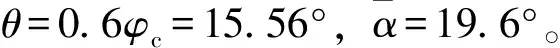
则按照本文公式和规范法公式分别计算得到的第2监测断面的破裂角、侧压力系数见表1；由此分别计算的围岩压力见表2，为了对比分析，将现场实测的初支围岩压力也列于表2中。由表2可知：本文公式的计算结果比规范法更接近实测值，说明在浅埋偏压隧道情况下，本文方法具有更好的实用性。

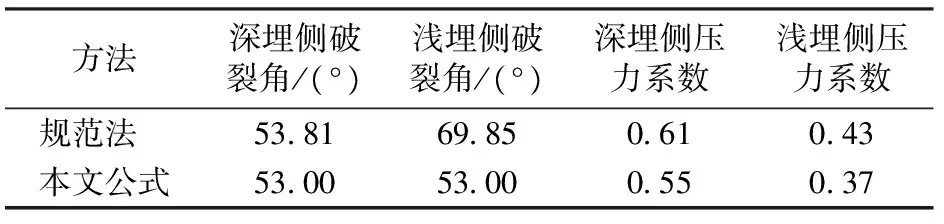
表1　第2监测断面的破裂角和侧压力系数

表2　围岩压力的理论值与实测值　kPa

5　结　语

本文根据极限平衡法，推导出了变坡面条件下浅埋偏压隧道松动围岩压力的计算公式，计算公式可以看作是对规范法中的侧压力系数公式进行了修正，也就是本文考虑了真实的坡面情况。根据推导的公式分析地表坡度变化对水平侧压力系数的影响可知：当变坡面角度增大时，水平侧压力系数增大，两侧土体对拱顶上覆土层的推力增大，拱顶垂直土压力减小，隧道水平侧压力增大。以贵广高铁贺街隧道为例，本文公式的计算结果比规范法计算结果更加接近实测值，验证了本文公式的有效性和合理性；在实际工程中，当隧道两侧土体坡度变化较大时，本文公式的计算结果更加切合实际。本文公式形式简洁、全面，可供相关人员进行工程精确计算。

[1]TERZAGHI K，TERZAGHI K，ENGINEER C，et al. Theoretical Soil Mechanics[M]. New York：John Wiley & Sons，1943.

[2]王毅才. 隧道工程[M]. 北京：人民交通出版社，2006.

[3]谢家烋. 浅埋隧道的地层压力[J]. 土木工程学报，1964(6)：58-70.

(XIE Jiaxiu. Earth Pressure on Shallow Burial Tunnel [J]. China Civil Engineering Journal， 1964 (6)：58-70.in Chinese)

[4]铁道第二勘察设计院. 铁路隧道设计规范[S]. 北京：中国铁道出版社，2005.

[5]SLOAN S W. Upper Bound Limit Analysis Using Finite Elements and Linear Programming[J]. International Journal for Numerical and Analytical Methods in Geomechanics，1988(12)：61-77.

[6]SLOAN S W. Upper Bound Limit Analysis Using Finite Elements and Linear Programming [J]. International Journal for Numerical and Analytical Methods in Geomechanics，1989(13)：263-282.

[7]邱业建，彭立敏，雷明锋. 浅埋偏压隧道围岩压力上限法解析解[J]. 土木工程学报，2015，48(6)：106-113.

(QIU Yejian，PENG Limin，LEI Mingfeng. Upper Bound Solutions for Surrounding Rock Pressure of Shallow Bias Tunnel [J]. China Civil Engineering Journal，2015，48(6)：106-113.in Chinese)

[8]LECA E，DORMIEUX L. Upper and Lower Bound Solutions for the Face Stability of Shallow Circular Tunnels in Frictional Material[J]. Geotechnique，1990，4(40)：581-606.

[9]赵炼恒，黄阜，孙秋红，等. 浅埋偏压矩形单洞隧道围岩压力极限上限分析方法[J]. 中南大学学报：自然科学版，2014,45(9)：3093-3104.

(ZHAO Lianheng，HUANG Fu，SUN Qiuhong，et al. Rock Pressure of Unsymmetrical Shallow Rectangular Tunnel Based on Upper Bound Limit Analysis Method[J]. Journal of Central South University:Science and Technology，2014,45(9)：3093-3104.in Chinese)

[10]杨峰. 浅埋隧道围岩稳定性的极限分析上限法研究[D]. 长沙：中南大学，2010.

(YANG Feng. Investigation of Shallow Tunnel Stability Using Upper Bound Solution of Limit Analysis[D]. Changsha：Central South University，2010.in Chinese)

[11]LEI Mingfeng，PENG Limin，SHI Chenghua. Model Test to Investigate the Failure Mechanisms and Lining Stress Characteristics of Shallow Buried Tunnels under Unsymmetrical Loading[J]. Tunnelling and Underground Space Technology，2015，46：64-75.

[12]王志伟，乔春生，宋超业. 上软下硬岩质地层浅埋大跨隧道松动压力计算[J]. 岩土力学，2014，35(8)：2342-2353.

(WANG Zhiwei，QIAO Chunsheng，SONG Chaoye. Calculation Method of Relaxation Pressure of Shallow Large Span Tunnel in Up-Soft/Low-Hard Rock Stratum[J]. Rock and Soil Mechanics，2014，35(8)：2342-2353. in Chinese)

[13]李鹏飞，周烨，伍冬. 隧道围岩压力计算方法及其适用范围[J]. 中国铁道科学，2013，34 (6)：55-60.

(LI Pengfei，ZHOU Ye，WU Dong. Calculation Methods for Surrounding Rock Pressure and Application Scopes [J]. China Railway Science，2013，34(6)：55-60. in Chinese)

[14]刘小军，张永兴，黄达. 破碎围岩浅埋偏压隧道衬砌荷载的计算方法[J].土木建筑与环境工程，2011，33(5)：28-33.

(LIU Xiaojun，ZHANG Yongxing，HUANG Da. Load Calculation Method of Shallow Tunnel under Unsymmetrical Loadings in Broken Surrounding Rock [J]. Journal of Civil, Architectural & Environmental Engineering，2011，33(5)：28-33. in Chinese)

[15]LEI Mingfeng，PENG Limin，SHI Chenghua. Calculation of the Surrounding Rock Pressure on a Shallow Buried Tunnel Using Linear and Nonlinear Failure Criteria[J]. Automation in Construction，2014，37:191-195.

[16]程小虎. 改进的浅埋隧道松动围岩压力计算方法[J]. 铁道学报，2014，36(1)：100-106.

(CHENG Xiaohu. An Improved Method to Calculate the Loosening Earth Pressure on Shallow Tunnels [J]. Journal of the China Railway Society，2014，36(1)：100-106. in Chinese)

[17]邓之友. 浅埋偏压隧道结构荷载反分析研究[D].长沙：中南大学，2012.

(DENG Zhiyou. Back-Analysis on the Structural Load of Shallow-Buried Tunnel[D]. Changsha：Central South University，2012.in Chinese)

[18]蔡来炳. 软弱围岩浅埋偏压连拱隧道力学效应研究[D]. 上海：同济大学，2008.

(CAI Laibing. Research on the Mechanical Behavior of Unsymmetrical Loading Twin-Arched Tunnels Located on the Shallow Weak Rock Mass[D]. Shanghai：Tongji University，2008.in Chinese)

[19]万小明.大断面浅埋软弱围岩隧道围岩变形规律分析研究[D]. 广州：广州工业大学，2012.

(WAN Xiaoming. Research on Deformation Laws of Large Cross Section Shallow Soft Surrounding Rock Tunnel[D]. Guangdong：Guangdong University of Technology，2012.in Chinese)