路基压实质量连续检测参数的空间分布特征分析

聂志红，谢　扬，焦　倓

(中南大学 土木工程学院，湖南 长沙　410075)

路基压实质量连续检测技术是将压路机与路基作为一个动力系统，利用振动轮的动力学参数与路基压实状态的关系，分析振动轮动态响应信号确定路基的压实程度，从而实现对整个碾压面进行压实质量检测[1-2]。目前，国内外已有的压实质量连续检测参数主要有CMV，CCV，Evib，ks等[3]。

振动压路机采集压实质量连续检测参数的过程中，由于碾压材料的非均质各向异性、压实状况以及振动压路机连续检测工艺参数的差别和波动，使得压实质量连续检测参数在碾压面上产生较大的空间变异性[4]。明确压实质量连续检测参数变异的空间分布特征是对路基压实质量均匀性评价的基础[5]。目前一般将压实质量连续检测参数作为纯随机变量，通过分析压实质量连续检测参数的均值、异常值及变异系数等经典概率统计量对路基压实均匀性进行评价[6]。但这些经典概率统计量不能充分发掘大量压实质量连续检测参数的内在规律以及空间分布特征，仅能从总体上对路基压实质量进行评价，难以准确反映每个区域路基压实质量的真实情况。

本文以沪昆高铁客运专线芷江试验段压实质量连续检测数据为基础，以压实计值CMV为例，基于地统计学方法，考虑压实质量连续检测参数空间分布的随机性和结构性[7]，用探索性数据分析方法分析连续压实检测数据，拟合其参数的半变异函数模型，分析其空间分布特征。

1　数据来源

CMV是振动压路机在振动过程中采集的振动轮竖向加速度信号，通过Fourier变换，经式(1)计算得到的[8]。

(1)

式中：C为常数；A2Ω为碾压加速度的一次谐波振幅；AΩ为碾压加速度的基波振幅。

试验段采用的振动压路机型号为BM 219DH—3，其具体技术参数见表1。压实质量连续检测设备使用CCS900信号采集系统，振动压路机沿着碾压带进行压实质量连续检测时，需保持振动压路机正向行驶且振动频率稳定，每20 cm将产生1个CMV，试验段采用破碎的砂质板岩作为填料，其物理指标见表2。

表1　振动压路机技术参数

表2　填料物理指标

试验段的有效碾压面为30 m×30 m的区域，根据碾压面宽度和振动压路机轮宽将碾压面划分为15条碾压轮迹，即每条碾压轮迹宽2 m，以便确保碾压轮迹覆盖整个碾压面[9]，如图1所示。

图1　碾压轮迹

2　探索性数据分析方法

探索性数据分析是对试验数据的性质进行全面深入的研究，充分发掘其在结构以及分布方面的特点和模式的分析方法[10]。

2.1　频率分布验证

利用地统计学方法进行CMV空间分布特征分析时，要求数据符合正态分布，否则将会产生比例效应[11]，降低模型估计精度，导致压实质量连续检测参数空间分布的结构特性不明显。因此在进行空间数据分析前，首先需要采用Kolomogorov-Semirnov(KS)检验[12]对采集的原始数据的分布结构进行正态分布检验。

2.2　空间自相关性分析

空间自相关性是不同空间位置上同一属性相似程度的度量。实验数据具有空间自相关性是进行地统计分析和构建空间模型的前提条件。全局Moran’s Ⅰ系数是衡量空间自相关性的常用指标，它反映了空间邻近区域参数的相似程度，其计算公式为

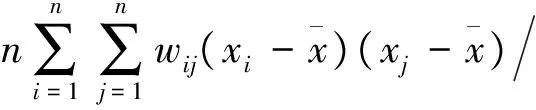
(2)

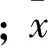
2.3　空间变异性分析

半变异函数是地统计学研究土体空间变异性的关键函数，它能够描述土体性质的空间连续变异以及土体性质随不同观测距离的变化特征，因此半变异函数可用于研究CMV的空间分布特征，并同时反映CMV的随机性变化和结构性变化[14]。半变异函数的计算公式为

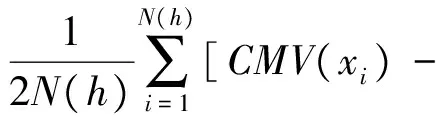
CMV(xi+h)]2

(3)

式中：h为样本点间距， 即步长；N(h)为样本点对的个数；CMV(xi)和CMV(xi+h)分别为CMV(x)在xi和xi+h位置处的实测值。

半变异函数理论模型中的变程、基台值和块金常数等能够反映CMV的空间分布特征。当样本点间距h超过一定值a(a>0)后，半变异函数γ(h)将趋于一稳定值C0+C，此处a被定义为变程，反映检测数据在空间上的自相关范围；C0+C被定义为基台值，反映检测数据总体变异程度，其中变异函数模型中的块金常数C0表示检测数据随机性变异程度，偏基台值C表示检测数据结构性变异程度。

3　CMV空间分布特征分析

为直观地观察CMV的分布规律，现将其碾压6遍后采集得到的CMV沿纵向的分布绘制成图，如图2所示。

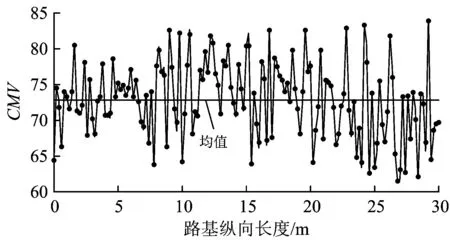
图2　CMV分布图

3.1　CMV频率分布验证

对检测数据进行单样本Kolomogorov-Semirnov检验，其双侧渐进显著性大小为0.30(>0.05)，同时绘制出的检测数据频率直方图如图3所示，进行正态分布拟合，其相关系数为0.91，表明检测数据服从正态分布[15]，满足地统计学和半变异函数建模的要求。

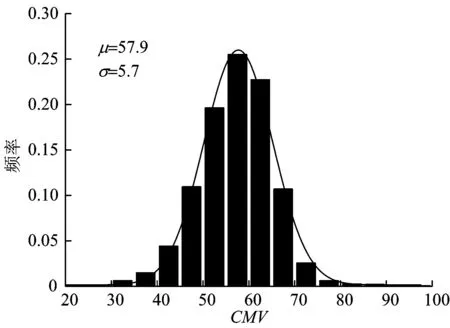
图3　CMV频率分布图

3.2　CMV空间自相关性分析

取整个平面内的检测数据，对其进行空间自相关性Moran’s Ⅰ系数计算，并绘制Moran’s Ⅰ系数随空间距离的变化趋势图如图4所示。

Moran’s Ⅰ系数的取值范围为[-1， 1]，若Moran’s Ⅰ系数大于零，则表明在距离h范围内的CMV存在空间正相关；且Moran’s Ⅰ系数越接近于0，其相关性越小[16]。由图4可知，研究区域内CMV的Moran’s Ⅰ系数大于0，且随着距离h的增大，其Moran’s Ⅰ系数逐渐减小，当h增大至14 m时，其Moran’s Ⅰ系数已趋近于0，表明研究区域内的CMV具有空间正相关性，且其空间正相关性随着距离h的增加而逐渐降低，CMV的最大自相关距离约为14 m。

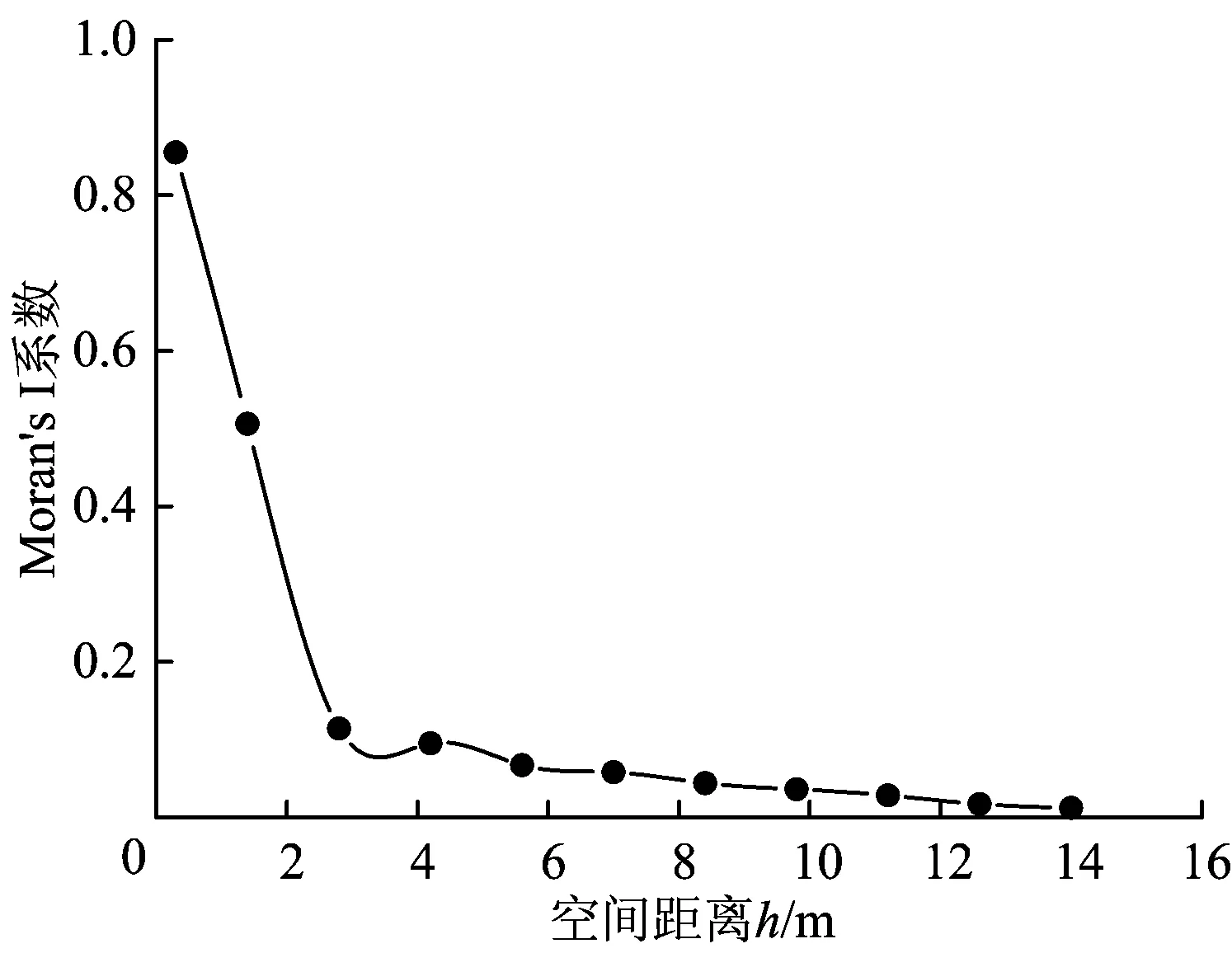
图4　Moran’s Ⅰ系数变化趋势图

3.3　压实质量连续检测参数空间变异及分布特征

分别取碾压6遍后路基纵向和横向的CMV值，根据指数型半变异函数γ(h)计算式(4)计算CMV的γ(h)，并根据其拟合出半变异函数曲线，建立CMV沿路基纵向和横向的指数型半变异函数模型，其结果如图5所示。

(4)

图5　半变异函数图

由半变异函数模型拟合结果可知，2个模型的相关系数分别达到了0.94和0.95，说明指数型半变异函数模型能够较好地拟合理论和试验半变异函数的关系。比较CMV沿路基纵向和横向的基台值发现，CMV沿路基横向的基台值较大，说明CMV沿路基横向具有更大的变异性。

变异程度C/(C0+C)是偏基台值与基台值之比，它表示变量的空间变异特性，即由结构性变异引起总变异的比重。该比值越高说明结构性变异部分占系统总变异的程度越大。当变异程度C/(C0+C)小于25%、或在25%～75%之内、或大于75%时，分别表示变量具有较弱、中等和较强的结构性变异[17]。计算所得路基纵向和路基横向CMV的变异程度分别为71.7%和86.4%，说明CMV沿路基纵向具有中等的结构性变异，而CMV沿路基横向具有较强的结构性变异；CMV沿路基横向比其沿路基纵向具有更强的结构性变异。

4　结　论

(1)Kolomogorov-Semirnov检验结果表明采集到的CMV服从正态分布，满足半变异函数建模的前提条件。

(2)分析全局Moran’s Ⅰ系数的结果表明，研究区域内CMV具有空间正相关性，且其空间正相关性随着空间距离的增加而逐渐降低，CMV的最大自相关距离约为14 m。

(3)建立的CMV沿路基纵向和路基横向的指数型半变异函数模型拟合程度高，能够较好地反映出CMV的空间变异情况及空间分布特征。CMV沿路基横向具有更大的变异性和空间相关性。

(4)压实质量连续检测参数的探索性数据分析结果表明，检测数据能够较好地满足进行地统计分析和半变异函数建模的前提条件。直观地得到了压实质量连续检测参数的空间分布规律，为路基压实质量的均匀性评价提供了一定的理论基础。

[1]聂志红，焦倓，王翔.基于谐波平衡识别法的铁路路基连续压实指标研究[J].中国铁道科学，2016，37(3)：1-8.

(NIE Zhihong， JIAO Tan， WANG Xiang.Study on Continuous Compaction Indicator of Railway Subgrade Based on Harmonic Balance Identification Method [J].China Railway Science，2016，37(3)：1-8.in Chinese)

[2]聂志红，焦倓，王翔，等.压实质量连续检测指标概率分布模型研究 [J].郑州大学学报：工学版，2014，35(2)：15-18.

(NIE Zhihong， JIAO Tan， WANG Xiang，et al.Study on Probability Distribution Models of Continuous Compaction Indicators [J].Journal of Zhengzhou University：Engineering Science， 2014，35(2)：15-18. in Chinese)

[3]MOONEY M A.Intelligent Soil Compaction Systems[M].Washington,D.C.:Transportation Research Board， 2010.

[4]张征， 刘淑春， 鞠硕华.岩土参数空间变异性分析原理与最优估计模型 [J]. 岩土工程学报， 1996， 18(4) ：43-50.

(ZHANG Zheng， LIU Shuchun， JU Shuohua. The Optimum Estimation Model and the Principle of Spatial Variability Analysis of Rock and Soil Parameters [J]. Chinese Journal of Geotechnical Engineering， 1996， 18(4)：43-50. in Chinese)

[5]FACAS N W， MOONEY M A， FURRER R. Anisotropy in the Spatial Distribution of Roller-Measured Soil Stiffness [J]. International Journal of Geomechanics， 2009， 10(4)： 129-135.

[6]聂志红， 焦倓， 王翔. 基于地统计学方法的铁路路基压实均匀性评价 [J]. 中国铁道科学， 2014， 35(5)：1-6.

(NIE Zhihong， JIAO Tan， WANG Xiang. Compaction Uniformity Evaluation of Railway Subgrade Based on Geostatistics [J]. China Railway Science， 2014， 35(5)： 1-6. in Chinese)

[7]VENNAPUSA P K R， WHITE D J， MORRIS M D. Geostatistical Analysis for Spatially Referenced Roller-Integrated Compaction Measurements [J].Journal of Geotechnical and Geoenvironmental Engineering， 2009， 136(6)：813-822.

[8]ADAM D. Roller Integrated Continuous Compaction Control (CCC) Technical Contractual Provisions & Recommendations [J]. Design and Construction of Pavements and Rail Tracks: Geotechnical Aspects and Processed Materials， 2007,10(9)： 111-138.

[9]中华人民共和国铁道部.TB 10108—2011 铁路路基填筑工程连续压实控制技术规程[S].北京：中国铁道出版社，2011.

[10]王喜， 秦耀辰， 张超. 探索性空间分析及其与GIS 集成模式探讨 [J]. 地理与地理信息科学， 2006， 22(4)：1-5.

(WANG Xi， QIN Yaochen， ZHANG Chao. Preliminary Discussion for Exploratory Spatial Data Analysis and the Integration Model with GIS [J]. Geography and Geo-Information Science， 2006， 22(4)： 1-5. in Chinese)

[11]李亮亮， 依艳丽， 凌国鑫， 等. 地统计学在土壤空间变异研究中的应用 [J]. 土壤通报， 2005， 36(2)：265-268.

(LI Liangliang， YI Yanli， LING Guoxin， et al. Utilization of Geostatistics in Soil Spatial Variability [J]. Chinese Journal of Soil Science， 2005， 36(2)： 265-268. in Chinese)

[12]丁晓波， 徐兴忠. 基于Kolmogorov-Smirnov统计量的连续置信带 [J]. 北京理工大学学报， 2008， 28(10)： 927-929.

(DING Xiaobo，XU Xingzhong.Continuous Confidence Bands Based on Kolmogorov-Smirnov Statistics [J]. Transactions of Beijing Institute of Technology， 2008， 28(10)：927-929. in Chinese)

[13]陈绍宽， 韦伟， 毛保华， 等. 基于改进时空Moran’s Ⅰ指数的道路交通状态特征分析 [J]. 物理学报， 2013， 62(14)：527-533.

(CHEN Shaokuan，WEI Wei，MAO Baohua， et al. Analysis on Urban Traffic Status Based on Improved Spatio-Temporal Moran’s Ⅰ[J]. Acta Physica Sinica， 2013， 62(14)：527-533. in Chinese)

[14]MATHERON G. Principles of Geostatistics [J]. Economic Geology， 1963， 58(8): 1246-1266.

[15]STEIN C M. Estimation of the Mean of a Multivariate Normal Distribution [J]. The Annals of Statistics， 1981,9(6)： 1135-1151.

[16]ASSUNCAO R M， REIS E A. A New Proposal to Adjust Moran’s Ⅰ for Population Density [J]. Statistics in Medicine， 1999， 18(16): 2147-2162.

[17]王卫华， 王全九， 武向博， 等. 黑河中游绿洲麦田土壤水气热参数田间尺度空间分布特征 [J]. 农业工程学报， 2013， 29(9)： 94-102.

(WANG Weihua， WANG Quanjiu， WU Xiangbo， et al. Characteristics of Spatial Distribution of Soil Water-Air-Heat Parameters in Typical Oasis Croplands at Middle Reaches of Heihe River [J]. Transactions of the Chinese Society of Agricultural Engineering， 2013， 29(9)：94-102. in Chinese)