高速铁路地震预警震级快速准确预测方法
王子珺,赵伯明
(北京交通大学 土木建筑工程学院,北京 100044)
地震预警作为能够有效减少地震灾害的重要手段之一,已经尝试应用于包括高铁在内的生命线工程和高危行业[1]。高铁预警系统一旦发生强震漏报或误报将会导致重大灾害事件,因此如何通过高铁监测网络中单台站获取的地震事件初始信息快速准确地进行地震震级的预测,是高铁地震预警系统中亟待解决的关键科学问题。
利用地震波初始信息估计整个地震过程中产生的能量(震级)是地震震级快速准确预测的基础,以下2种理论为上述地震震级的预测提供了依据。第1种是成核震相的理论,Nakatani等[2]认为在统计意义上,地震初始破裂的形态与最终规模取决于地震在一定空间域和时间域内的成核过程。第2种是地震的P波、S波理论,Kanamori等[3]指出P波中携带的信息反映了断层的震源机制,而S波则反映了地震的最终能量。
1 地震数据与数据预处理
中国数字强震动台网在2008年汶川Ms8.0级地震中获得了大量的强震观测记录[4]。由于同一次地震在指定范围内有多个台站获得了加速度记录,便于研究不同因素对震级预测的影响,因此本文从强震观测记录中选取了汶川地震的主震及其37个余震记录作为研究的数据样本。地震记录的筛选条件为震级大于Ms4.0且震中距小于100 km。由于地震记录中垂直分量的P波最为发育且震相相对清晰,因此选择垂直分量的加速度进行相关特征参数的计算并开展地震预警的研究,最终使用并解析了50个台站的272条满足要求的加速度记录。
观测台网所使用的仪器均为安装于自由地表的数字强震仪,采样频率为200 Hz,测量范围为±2g。数据预处理工作包括:首先将原始的加速度记录减去记录全长的平均值,完成基线调零;对调零后的加速度积分1次得到速度,将速度积分1次得到位移;对处理后的加速度、速度和位移分别进行0.075 Hz的二阶Butterworth高通滤波,以去除记录的低频漂移。将预处理后的数据分别称为加速度时程、速度时程和位移时程。
2 震级预测方法与比较
2.1 位移平方积分参数的提出
由于特征参数的计算依赖于对初始P波的精确拾取,因此采用开发的三步骤P波及S波复合自动快速识别方法[5],同时对每一条记录的P波到时进行二次人工读取验证。在得到初始P波到时ti的基础上,选择3 s的计算时间窗,应用2008年汶川Ms8.0级地震的加速度记录,分别对常用的特征参数进行分析考察。在此基础上,参照速度平方积分参数的形式,提出位移平方积分WISD参数,其定义如下。
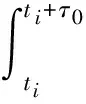
(1)
式中:τ0为积分区间的时间窗长,取为3 s;u为地面位移。
由位移平方积分WISD的定义式(1)可知,该物理量能够反映地震早期辐射出的能量大小,作为预测震级的参数,其物理意义明确。Nielsen等认为[6],弹性能的能流密度可以控制地震破裂的发育以及传播过程,具有较高初始能量的破裂能够传播到更远的距离。由于能流密度与动态应力降以及破裂过程的几何尺寸有关,因此地震的最终震级与初始阶段应力降的水平或断层初始破裂面积间存在一定联系。
为了对提出的方法进行对比验证,选择2个准确性和稳定性都较好的代表性特征参数τc和Pd作为比较研究对象,基于本文的地震记录数据,利用最小二乘法分别对WISD,τc和Pd这3个特征参数与地震震级Ms进行拟合。在拟合过程中,由于地震成因的复杂性以及台站所在场地条件不同等因素,对于同一次地震,由不同台站的观测记录计算得到的特征参数之间也会存在一定差异,因此利用不同台站的特征参数的平均值进行数据拟合,可以有效降低拟合结果的离散性,提高结果的相关度。
2.2 位移平方积分WISD与震级的拟合关系
基于本文的地震记录数据,建立的位移平方积分WISD与震级Ms的拟合关系如式(2)所示,其拟合曲线如图1所示。
logWISD=-9.872+1.022Ms±0.425
(2)
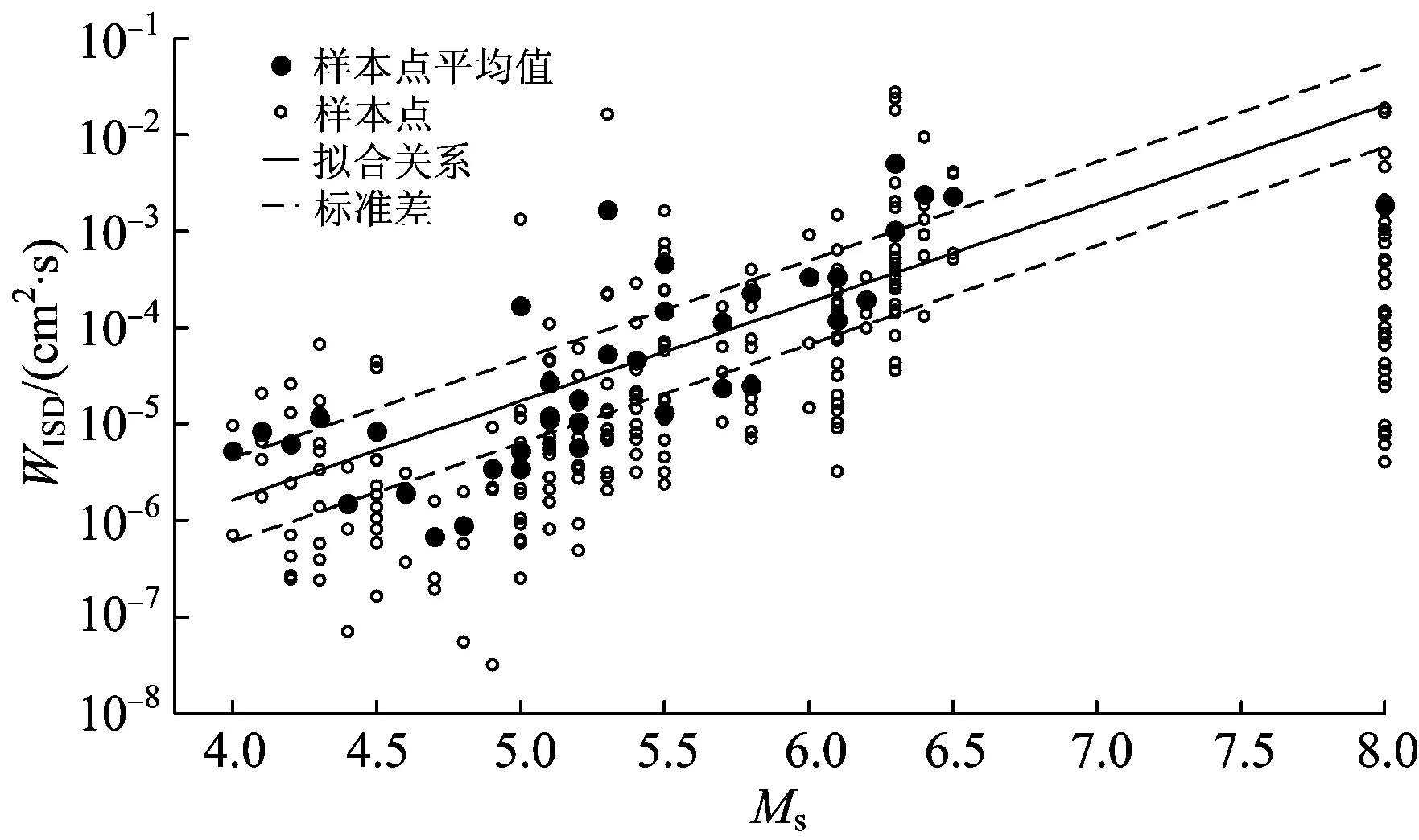
图1 位移平方积分WISD与震级Ms的拟合关系
由图1可知:WISD与Ms之间存在较好的线性关系;对于小于Ms6.5级的地震,由于其大部分的积累能量能够在较短的时间内释放,WISD与Ms的线性关系很好,离散性较小;而对于汶川地震Ms8.0级的主震,由于其前期释放的能量较少,因此利用该参数会出现震级低估的现象,即震级“饱和”现象。
2.3 平均周期τc与震级的拟合关系
logτc=-1.291+0.231Ms±0.151
(3)
由图2可知:τc与Ms之间存在较好的线性相关性;特别是对于Ms6.5级以下的地震,τc与Ms的线性相关性很好;同样,对于汶川地震Ms8.0级的主震也出现明显的震级低估现象。
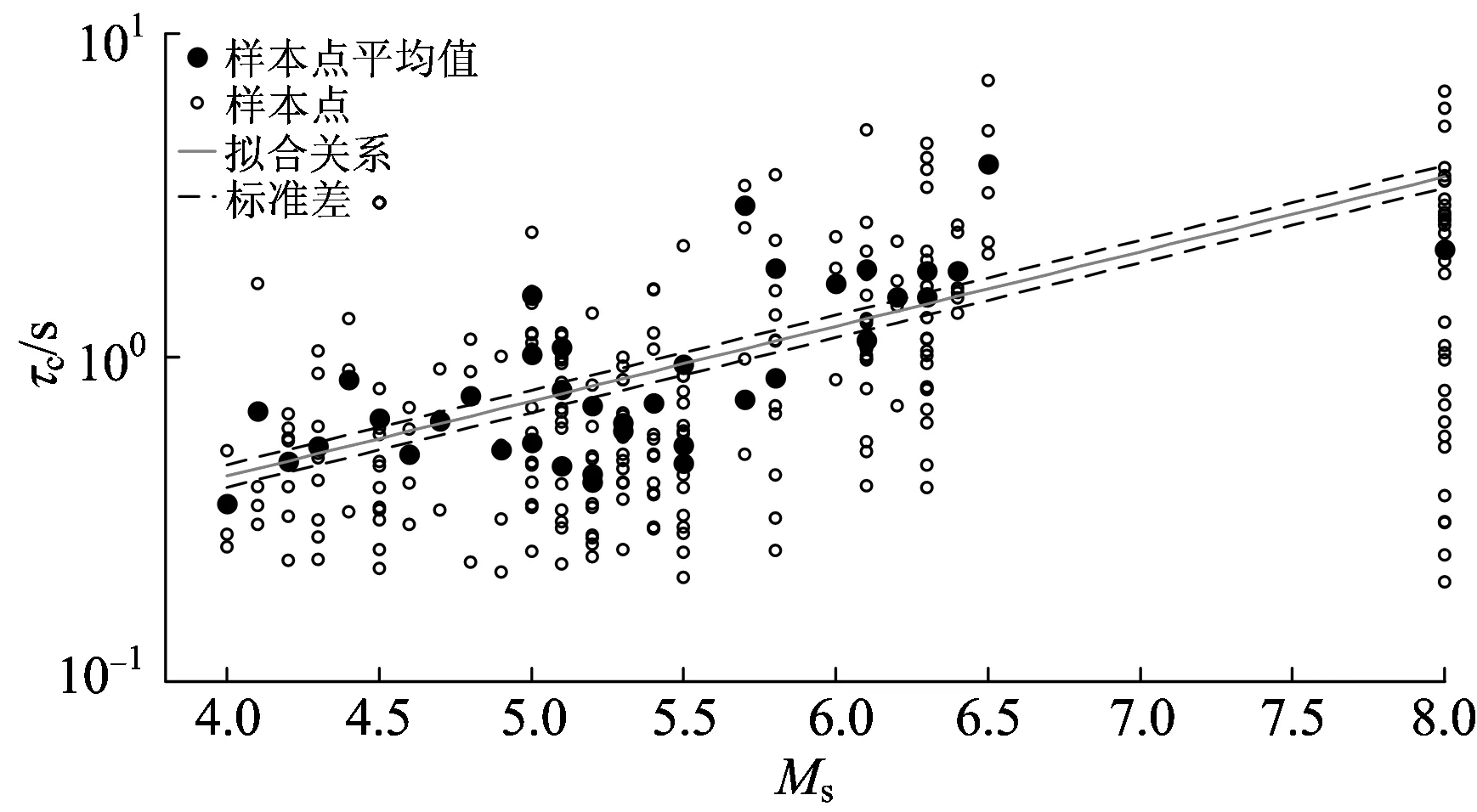
图2 平均周期τc与震级Ms的拟合关系
2.4 位移幅值Pd与震级的拟合关系
根据Wu与Zhao提出的Pd方法[7],为保证拟合结果的准确性,首先计算得到每一个台站所记录的地震事件的震源距R,然后进行回归分析计算。基于本文的地震记录数据,建立的位移幅值Pd与震级Ms和震源距的拟合关系如式(4)所示,其拟合曲线如图3所示。需要说明的是,汶川地震的余震中没有Ms7.0级的,所以图3中没有Ms6.5~Ms7.0级的数据点。
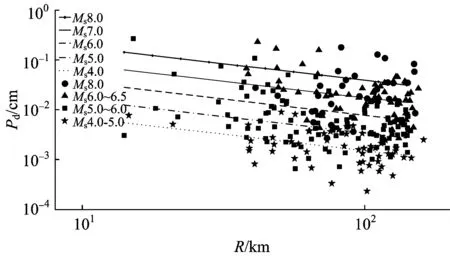
图3 不同震级Ms时位移幅值Pd与震源距R的拟合关系
logPd=-2.918+0.353Ms-
0.658logR±0.181
(4)
由图3可知:Pd与R之间存在较好的线性关系;同样,随着震级的增加,数据的离散性愈大,对于汶川地震Ms8.0级的主震,其拟合精度较差,也出现明显的震级低估现象。
2.5 地震震级预测
将以上3个特征参数应用于实际的地震预警中,根据每个参数与地震震级的回归关系表达式,可以分别推导得到以特征参数为已知量的地震震级预测公式,将3个预测公式得到的震级分别命名为位移平方积分震级MWISD,平均周期震级Mτc以及位移幅值震级MPd,并将MWISD,Mτc和MPd统称为M预测,则有
MWISD=9.660+0.979logWISD
(5)
Mτc=5.589+4.330logτc
(6)
MPd=8.258+2.830logPd+1.862logR
(7)
根据汶川地震主震及其37个余震记录,分别计算得到3个特征参数震级与实际震级的拟合关系,如图4所示。图中的45°线表示M预测=Ms,两侧的虚线分别表示正负1倍标准差。通过计算可得,本文提出的基于参数WISD预测的震级与实际震级的标准差为0.416,是三者中最小的;而Mτc和MPd与实际震级的标准差基本相同,分别为0.652和0.689。
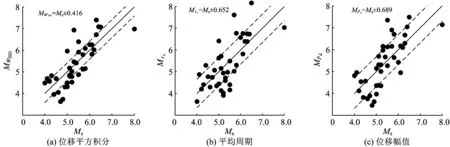
图4 3个特征参数预测震级与实际震级的比较
由图4可知:对于通过这3个特征参数推导的地震震级,绝大多数都在其对应震级的1倍标准差范围内;对于Ms6.5级以下的地震,利用初始P波前3 s信息得到的3个特征参数与震级之间存在良好的线性关系,可以通过建立的拟合公式对6.5级及以下级别的地震进行可靠稳定的预测;但是,对于汶川Ms8.0级主震,由3个特征参数推导的预测震级分别为MWISD=7.11,Mτc=7.04,MPd=7.15,均出现一定程度的震级“饱和”现象,即对于大震来说,采用较短的初始P波记录会造成对震级低估的现象,这一点可以通过等时线理论进行解释。等时线是指在一定时间内到达特定台站的一系列辐射能量点的集合,在断层产生P波后的短时间内,等时线即有可能覆盖辐射出高频地震动的断层区域。基于本文的计算结果,初始P波前3 s等时线包围的断层面积只能反映中强地震的最终断层尺度;而对于大地震(Ms6.5~Ms8.0级),初始P波前3 s内的信息不足以包含初始破裂的全部信息,导致出现预测震级“饱和”的结果。
2.6 预测结果比较分析
统计学中通常使用频率分布直方图来描述样本值的分布情况,进而根据直方图的轮廓得到近似密度函数曲线来研究总体的分布特征。因此,根据以上3个特征参数的地震震级预测式(5)—式(7),可以求出每一个地震记录的预测震级偏差值,即δ=M预测-Ms,通过验证相应的频率分布直方图可知预测震级的偏差基本符合正态分布,其概率密度函数p(x)为
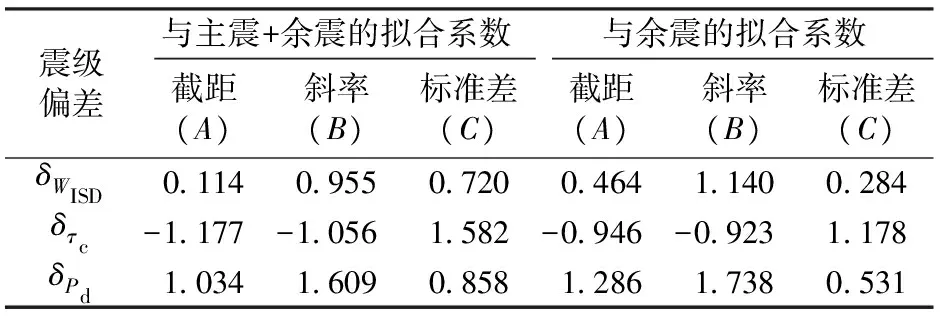
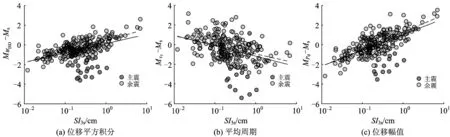
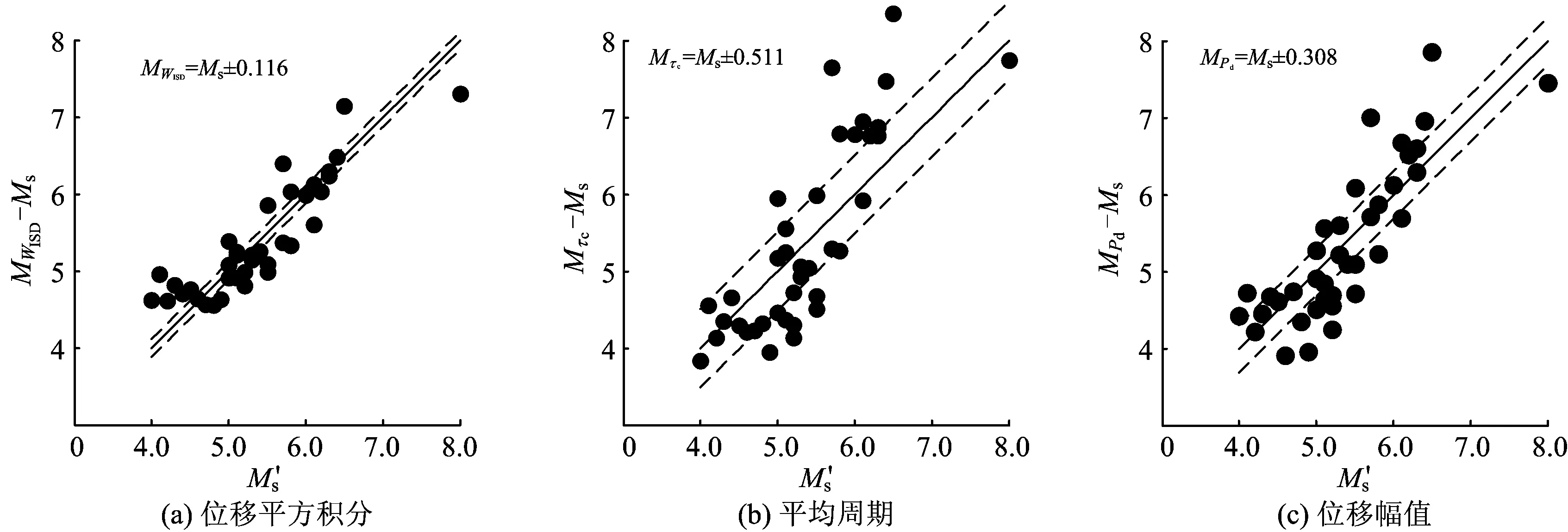
-∞ (8) 式中:x为样本值;m为样本值的数学期望;σ为标准差。 根据式(8)求解3个特征参数预测震级偏差的概率密度函数,并得到相应的概率密度曲线,如图5所示。由图5可知:本文提出的基于位移平方积分WISD预测震级方法,其震级偏差的标准差σ最小,即数据分布的离散性最小,且小偏差所占比例较高,说明较基于平均周期和位移幅值预测震级的2种方法,本文提出的基于WISD预测震级方法所得到的预测结果更精确。 图5 3个特征参数预测震级偏差的概率密度曲线对比 基于上述研究结果可知,利用初始P波计算的特征参数可以较为准确地预测地震的实际规模。但是部分预测结果表现出一定偏差,且对大地震的估计出现震级“饱和”现象。因此,为了进一步提高震级的预测精度,需要分析与预测偏差相关的影响因素,对震级预测公式提出适当的修正方法。由于频域分析与时域分析可以从不同角度把握地震动的固有特性,因此开展频域参数与预测震级偏差之间的相关性研究。 求解初始P波前3 s的谱强度SI3s[8],研究发现震级偏差δ和SI3s的对数值成一定的线性关系,因此,分别针对3个特征参数计算得到的震级偏差δ,利用最小二乘法对全部272个地震数据的震级偏差δ与SI3s进行回归拟合,拟合公式为 δ=A+BlogSI3s±C (9) 式中:A和B为待计算的回归系数;C为标准差。 在拟合过程中发现,主震的32个数据对于整体的拟合直线有一定的偏离,因此考虑对所有余震数据进行单独拟合。2种拟合的统计回归系数见表1,相应的拟合关系如图6所示。 表13个特征参数的预测震级偏差与3s谱强度对数的拟合系数 震级偏差与主震+余震的拟合系数与余震的拟合系数截距(A)斜率(B)标准差(C)截距(A)斜率(B)标准差(C)δWISD011409550720046411400284δτc-1177-10561582-0946-09231178δPd103416090858128617380531 利用3 s谱强度参数对偏差进行修正后的预测震级与实际震级的比较如图7所示。将图7与图4对比可知:修正后的3个特征参数震级与实际震级之间的偏差均有所降低,通过计算可知本文提出的WISD方法的标准差最小,仅为0.116个震级单位,而τc和Pd所对应的标准差分别为0.511和0.308;同时,对于汶川Ms8.0级主震的预测,震级“饱和”的现象均有所缓解,分别为MWISD=7.41,Mτc=7.74,MPd=7.46。 图6 3个特征参数的预测震级偏差与3s谱强度对数的拟合关系 图7 利用3 s谱强度参数修正后的3个特征参数预测震级与实际震级的比较 对于特征参数在估计大地震时出现的震级“饱和”现象,虽然可以采取增加时间窗长对P波信息进行连续追踪从而实时更新特征参数的办法,但是基于地震预警实时性和时效性的要求,需要利用尽可能短的时间准确确定地震震级等相关地震动参数,保证后续预警工作的顺利进行。因此,本文提出的修正方法可以更加快速且有效地对地震震级进行修正,从而达到准确的震级预测结果。 (1)针对我国高铁的特点,以及高铁地震预警对时间和精度的要求,基于沿线路排列的原位地震监测网络所必需的单台站预警模式,本文研究提出适合于高速铁路单台站快速准确进行地震震级预测的基于位移平方积分参数WISD的理论方法。 (2)利用2008年汶川Ms8.0级地震的主震及其余震记录272条,分别研究了位移平方积分WISD、平均周期τc和位移幅值Pd与地震震级之间的相关性,建立了3个特征参数与地震震级之间的拟合关系,推导得到相应的地震震级预测公式。 (3)提出了一种利用3 s谱强度SI3s对震级预测偏差进行修正的方法,该方法可以显著提高震级预测精度,同时缓解在预测大地震时出现的震级“饱和”现象。 (4)本文提出的基于位移平方积分WISD预测震级的方法与基于平均周期τc和基于位移幅值Pd预测震级方法的结果比较显示,基于WISD预测的震级偏差的标准差最小,预测结果的可信度最高,在应用提出的震级偏差修正方法后,其精度可进一步大幅提高,说明提出的基于WISD预测震级的方法能够更好地进行高速铁路的地震预警。 [1]NAKAMURA Y,SAITAJ,SATO T. On an Earthquake Early Warning System (EEW) and Its Applications [J]. Soil Dynamics and Earthquake Engineering,2011,31(2):127-136. [2]NAKATANI M,KANESHIMA S,FUKAO Y. Size-Dependent Microearthquake Initiation Inferred from High-Gain and Low-Noise Observations at Nikko District, Japan [J]. Journal of Geophysical Research Atmospheres,2000,105(B12):28095-28109. [3]KANAMORI H. Real-Time Seismology and Earthquake Damage Mitigation [J]. Annual Review of Earth and Planetary Sciences,2005,33:195-214. [4]国家强震动台网中心. 2008年汶川地震数据集[DB/OL]. [2015-11-01].ftp://www.csmnc.net. [5]王子珺,赵伯明. 高速铁路地震预警P波与S波复合自动快速识别的理论方法与应用[J]. 中国铁道科学,2016,37(4):121-127. (WANG Zijun,ZHAO Boming. Theatrical Method and Application of Auto-Rapid P and S Waves Recognition in Earthquake Early Warning for High Speed Railway[J]. China Railway Science,2016,37(4):121-127. in Chinese) [6]NIELSEN S. Can Earthquake Size be Controlled by the Initial Seconds of Rupture? [C]// GASPARINI P, MANFREDI G, ZSCHAU J. Earthquake Early Warning Systems. Berlin Heidelberg:Springer,2007:9-20. [7]WU YM,ZHAO L. Magnitude Estimation Using the First Three Seconds P-Wave Amplitude in Earthquake Early Warning [J]. Geophysical Research Letters,2006,33(16):L16312. [8]王子珺,赵伯明. 高速铁路地震预警线路场地地震动快速准确预测方法[J]. 中国铁道科学,2016,37(6):128-134. (WANG Zijun,ZHAO Boming. Fast and Accurate Prediction Method for Track Ground Motion in Earthquake Early Warning for High Speed Railways [J]. China Railway Science,2016,37(6):128-134. in Chinese)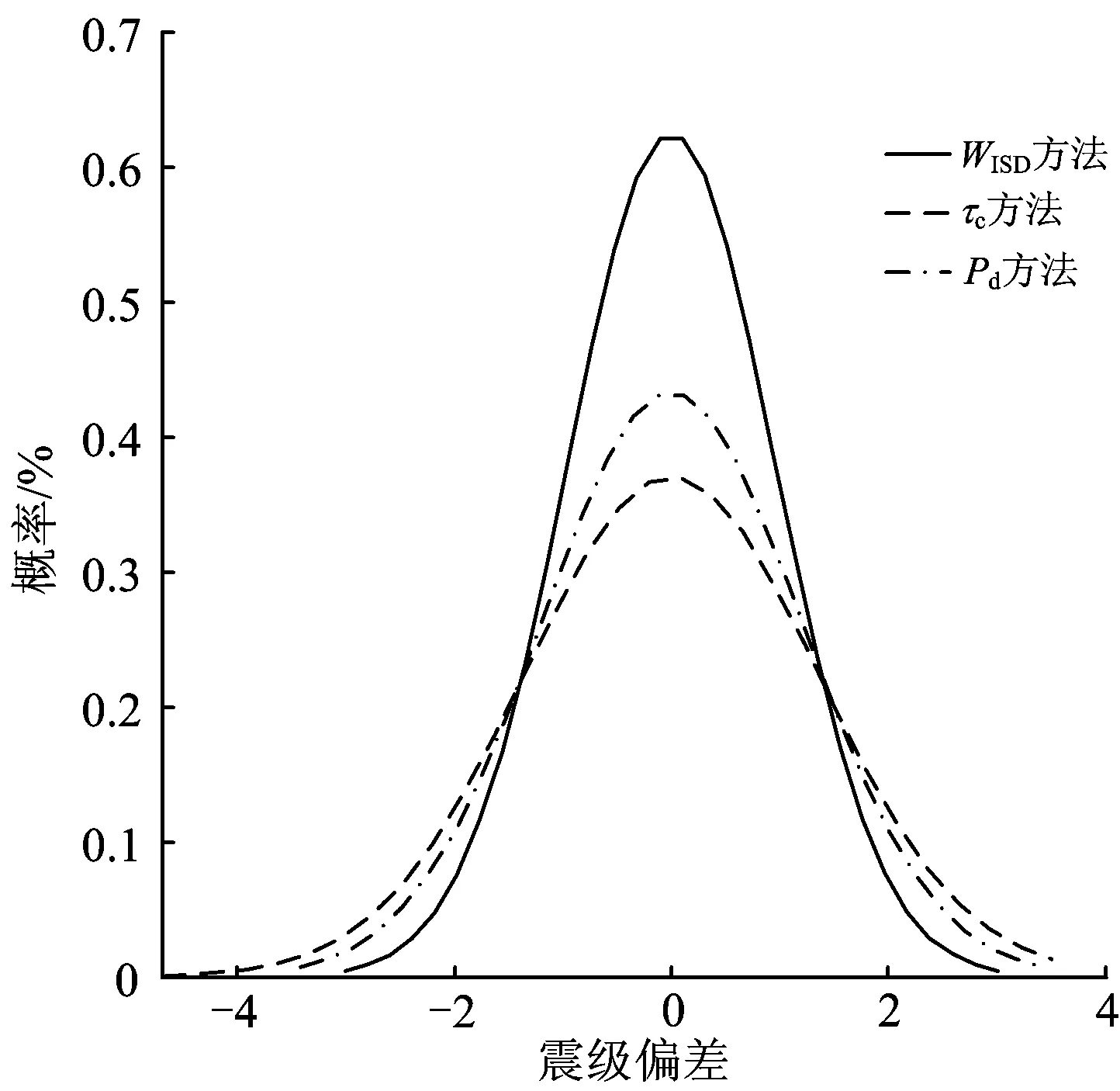
3 基于3 s谱强度预测震级偏差的修正方法
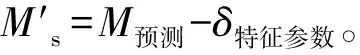
4 结 论

