高速铁路列车运行调整的模型及其策略优化方法
庄 河,何世伟,戴杨铖
(1.西南交通大学 交通运输与物流学院,四川 成都 610031; 2.中国铁路总公司 运输局,北京 100844;3.北京交通大学 交通运输学院,北京 100044)
高速铁路列车具有很高的正点率,但当受到设备故障、恶劣天气、突发事件等因素影响时,也会出现列车到达车站时刻偏离计划运行图的情况,因此需要对列车运行计划进行调整。
高速铁路列车运行调整具有约束条件复杂、优化指标多、实时性高、动态性强等特点。文献[1—3]采用基于列车到发车站时刻等决策值的方法进行列车运行调整优化;文献[4]构建了以最小化等待时间及最小化中高速列车总旅行时间的双目标优化模型,采用分支定界法与束搜索算法相结合的方法求解;文献[5]设计了基于替代图的列车运行调整计划编制模型及优化方法;文献[6]针对高速铁路列车运行调整复杂性高的特点,采用贪婪算法进行实时列车调整;文献[7]建立列车到发时刻与进路同步优化的高速铁路列车运行调整整数规划模型,设计了基于优先级规则的调度调整启发式算法;文献[8—9]采用以列车运行顺序为关注对象的序优化方法;文献[10—11]分别采用禁忌搜索算法和遗传算法进行列车运行调整。这些研究推进并丰富了列车运行计划调整的优化方法体系,数学模型也具有直观的优点,但由于这类数学模型变量多、构模与算法复杂,加上问题的动态性,很难得到令人满意的解,因此,亟须研究提出高速铁路列车运行计划调整的新方法。
策略是指对将来任意可能的状态可采取的行动的集合[12-13],如在生产调度工作中,可推迟加工设备的开、完工时间,可调整加工设备的加工顺序等。高速铁路列车运行调整优化问题与一般生产调度优化相通,如调度员确定相邻的相互冲突列车是顺晚、还是在前方站或后方站越行,就类似于生产调度的策略。基于策略的优化方法是指以策略而非传统决策值为对象的优化方法。有学者基于策略研究了高速铁路列车运行调整问题:文献[14]提出将客运专线列车运行调整问题转化为车间调度问题,并针对局部调整和大面积调整分别提出了实用可行的调整策略模型及算法。这些基于策略的研究成果,进一步拓展了高速铁路列车运行调整问题研究的思路,但多采用固定策略的仿真分析方法,使得各种调度策略之间缺乏衔接性和关联性,也无法保证解的优化质量。马氏决策过程模型通过揭示不同状态下优化策略与转移概率和获得报酬的关系,解决各种调度策略之间的衔接性和关联性问题,并在保证解的优化质量前提下简化计算过程,在很多领域得到了较好的应用[12-13]。因此,可基于马氏决策过程模型和策略优化方法研究高速铁路列车运行调整问题。
本文构建高速铁路列车运行调整问题的马氏决策过程模型;给出列车运行调整行动的最优策略条件,设计模型求解的策略优化方法;结合实际案例,将策略优化方法的求解结果与传统模型优化算法、人工调整方法的结果进行对比,以验证马氏决策过程模型和策略优化方法的正确性和有效性。
1 高速铁路列车运行调整马氏决策过程模型的构建
定义如下概念和参数:将高速铁路行车调度员对列车进行调整的时间点称为决策时刻,令T为所有决策时刻的集合,且T={0,1,2,…,e,…,E},E为阶段数或总时刻点数。在每个决策时刻e,设相邻且存在冲突的列车所在位置为状态ζe,S为高速铁路行车组织中列车的常见冲突状态集合,也称为状态空间,ζe∈S,S={1,2,3},其中“1”表示前、后列车同速,因前行列车晚点而导致的冲突(简称同速列车冲突),“2”表示前面为高速列车,后面为中速列车,前行列车晚点导致的冲突(简称高中速列车冲突),“3”表示前面为中速列车,后面为高速列车,前行列车晚点导致的冲突(简称中高速列车冲突)。
在状态ζe下,行车调度员可采取的调整措施称为行动a,A(ζe)为所有行动的集合,a∈A(ζe),A(ζe)={1,2,3},其中“1”表示后行列车顺晚(简称顺晚),“2”表示后行列车在冲突区间的前方站越行前行列车(简称前方站越行),“3”表示后行列车在冲突区间的后方站越行前行列车(简称后方站越行)。
在任意决策时刻e,状态为ζe,采取行动a后,下一个决策时刻系统所处的状态由概率分布p(·|ζe,a) 决定,以此时列车加权总晚点时间作为调度员采取行动将获得的报酬r(ζe,a),当报酬为正值时,表示列车调整的目标有改善(即加权总晚点时间减少),为负值时表示列车调整的目标进一步恶化。由于高速铁路列车运行调整决策过程符合马氏决策过程的重要特征,即列车状态的转移概率和报酬仅仅依赖于当前的状态和调度员采取的行动,而不直接依赖于以前的情况,则高速铁路列车运行调整问题的马氏决策过程模型为
{T,S,A(ζe),p(·|ζe,a),r(ζe,a)}
(1)
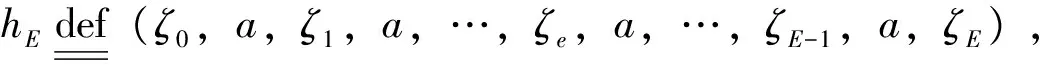
2 高速铁路列车运行调整马氏决策过程模型的最优策略条件
2.1 马氏决策过程模型策略的定义
对于马氏决策过程模型,有如下定义[12]。
定义1:如果状态空间下的函数f满足对每个ζe∈S有f(ζe)∈A(ζe),即f:S→A(ζe),则称f为确定性决策规则,也称为决策函数;全体决策函数所组成的集合记为F。
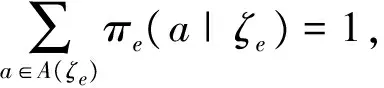
定义2:1个决策函数序列π=(f0,f1,f2,…,fe,…),fe∈F,e∈T,称为(确定性)1个马氏决策策略,其中fe是决策时刻e的决策函数,不依赖于决策时刻e以前系统的历史;全体马氏策略所组成的集合记做Πm,称为马氏策略类。
由于给定调整范围(时段、区间和列车数)的高速铁路列车运行调整优化问题属于有限状态、可数行动的情形,对其最优策略的结构有如下定理。

定理1的证明参见文献[15]。
定理2:1个马氏决策策略π=(f0,f1,f2,…,fe,…)∈Πm是1个最优策略的充要条件是:每个决策规则在每个可实现的历史上都要采取最优的行动。
定理2的证明参见文献[13]。
2.2 列车顺晚行动及其最优策略条件
定理3:在出现大面积列车晚点时,若所有列车本身均无故障,且所有列车晚点均未超过最大可接受晚点时间,则应采用列车顺晚依次开行的行动。
定理3的证明如下。
在决策时刻0,列车有3种冲突状态,即ζ0={1,2,3}。
状态1(ζ0=1,即同速列车冲突)如图1所示,2列列车的运行线为平行线。假设列车i晚点而列车j不晚点,并假设列车i在k+1站的晚点时间为tw,则对于后面的列车j,可根据车站间隔时间将其调整至当前可行的最早到达时间,调整时间为tx;因为之后对这2列车均可以通过压缩区间运行时间和车站停留时间来恢复其正点运行,故应采用列车顺晚依次开行的行动,不考虑列车越行。另一方面,假设列车i和列车j均晚点,此时,tx不仅可调整余地小,而且也不符合考虑列车越行问题的基本条件(晚点均未超过最大可接受时间),故应采用列车顺晚依次开行的行动,不考虑列车越行。
状态2(ζ0=2,即高中速列车冲突)如图2所示,前行的高速列车i在k+1站晚点tw,tx为中速列车j在k+1站的预计到达时间与高速列车i的实际到达时间之差,Idd为车站不同时到达最小间隔时间。若tx>Idd,则列车j不需要进行调整,否则,根据车站间隔时间把列车j调整至当前可行的最早到达时间即可,故应采用列车顺晚依次开行的行动,不考虑列车越行;之后列车i和列车j同样可以通过压缩区间运行时间和车站停留时间来恢复正点运行。这种冲突对后车带来的连带晚点影响最为轻微,若后行列车也晚点,则应采用列车顺晚依次开行的行动,更无需考虑列车越行。
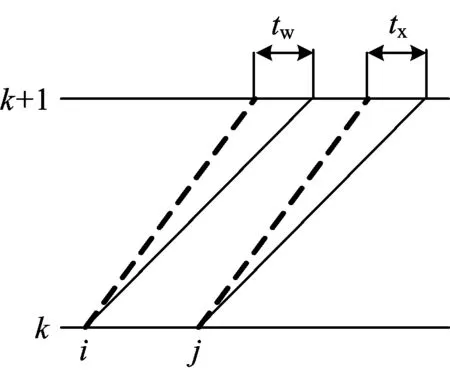
图1 同速列车顺晚依次开行
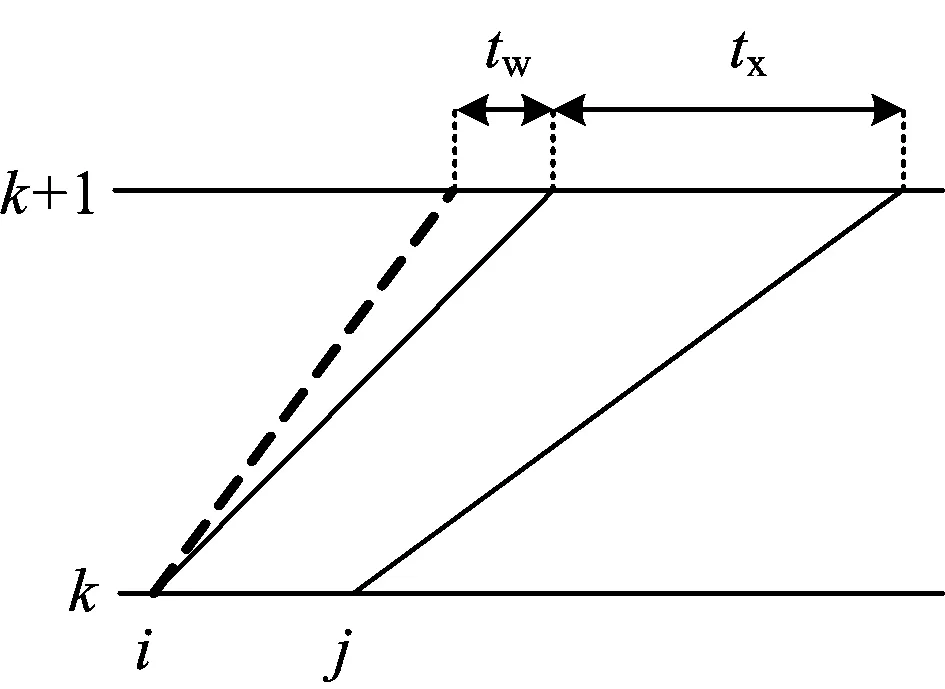
图2 高中速列车顺晚依次开行
状态3(ζ0=3,即中高速列车冲突)如图3所示,若前行的中速列车i在k+1站发生晚点,与后行的高速列车j在区间发生冲突,在不改变列车到发顺序的前提下,后行高速列车j只能根据车站间隔时间进行调整(减速慢行),调整时间tx。由图3可以发现,这种调整会大大限制列车j在区间的运行速度,并且下一区间依然会受到列车i的牵制,带来连带晚点影响。但根据定理3:对于大面积列车晚点,所有列车自身均无故障,且所有列车晚点均未超过最大可接受时间,此时由于后续高速列车也同样晚点,导致tx大大减少,甚至为0,因此,该情况下仍应采用列车顺晚依次开行的行动,无需考虑列车越行。只有当后行的高速列车晚点时间超出最大可接受时间时,才有必要考虑列车越行。
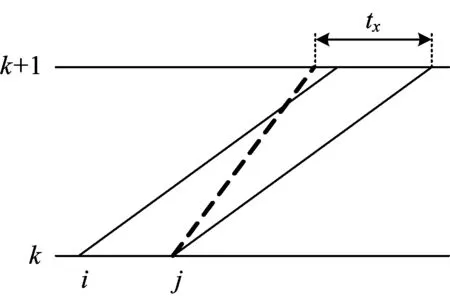
图3 中高速列车顺晚依次开行
综上,在决策时刻0时,对于列车冲突的3种冲突状态ζ0,所采取的最优行动均为列车顺晚依次开行。
采用同样的分析方法可得,在任意决策时刻e,对于列车冲突的3种状态ζe,所采取的最优行动仍为列车顺晚依次开行。
由此可得,在0,1,2,…,e,…,E序列决策时刻中,对于列车冲突的3种冲突状态,所采取的最优行动均为列车顺晚依次开行。
根据定理1和定理2,1个决策策略是最优策略的充要条件就是每个决策规则在每个可实现的历史上都要采取最优的行动,由于上述讨论的每个行动均为最优且符合最优平稳策略的条件,故定理3得证。
2.3 列车越行行动及其最优策略条件
当前行列车出现严重晚点或列车晚点超过最大可接受时间,而后行列车运行没有晚点或者晚点较少,不符合列车顺晚依次开行行动的最优策略条件时,就需要考虑相邻冲突列车间的越行问题。在讨论列车越行行动前,先给出如下定义。
定义4:在状态ζe下,若2列列车在区间发生冲突,对于后行列车是在前方站越行(行动2,a=2)还是在后方站越行(行动3,a=3),是由采取该行动所获得的行动报酬决定的,行动报酬较大的行动则为状态ζe下的最优行动。
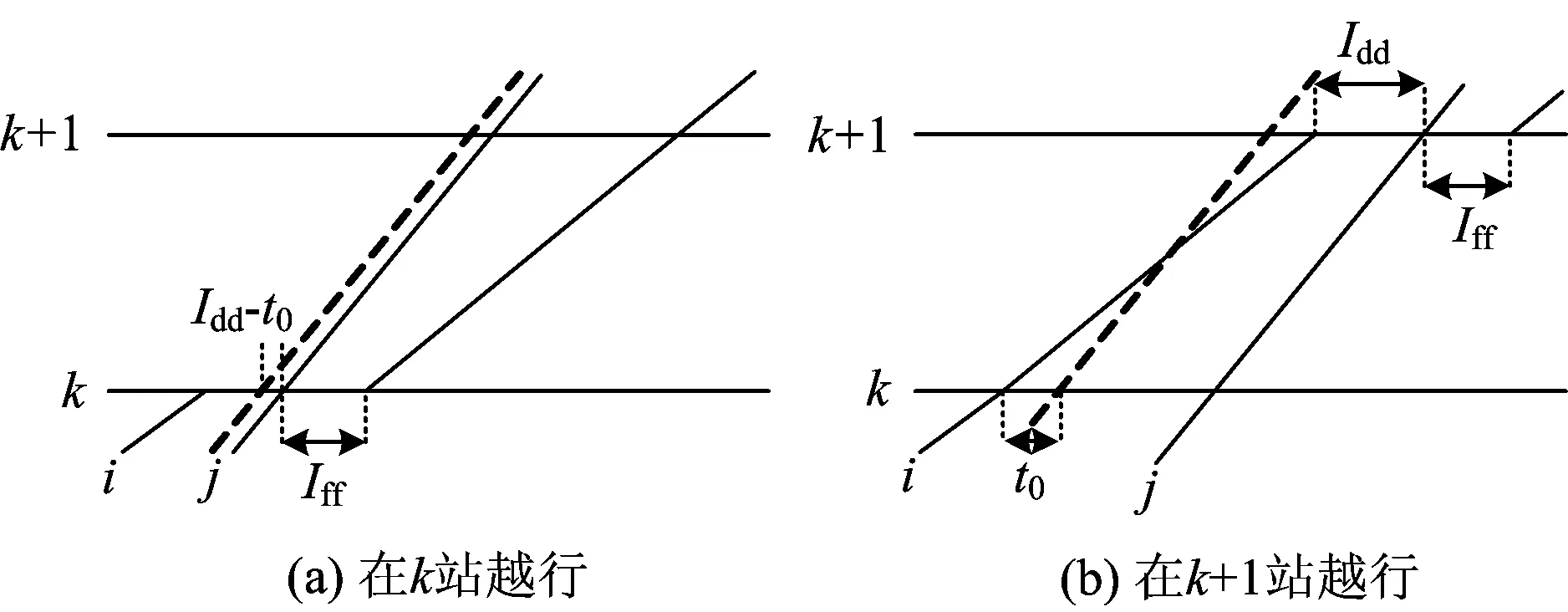
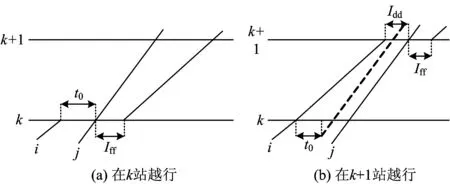
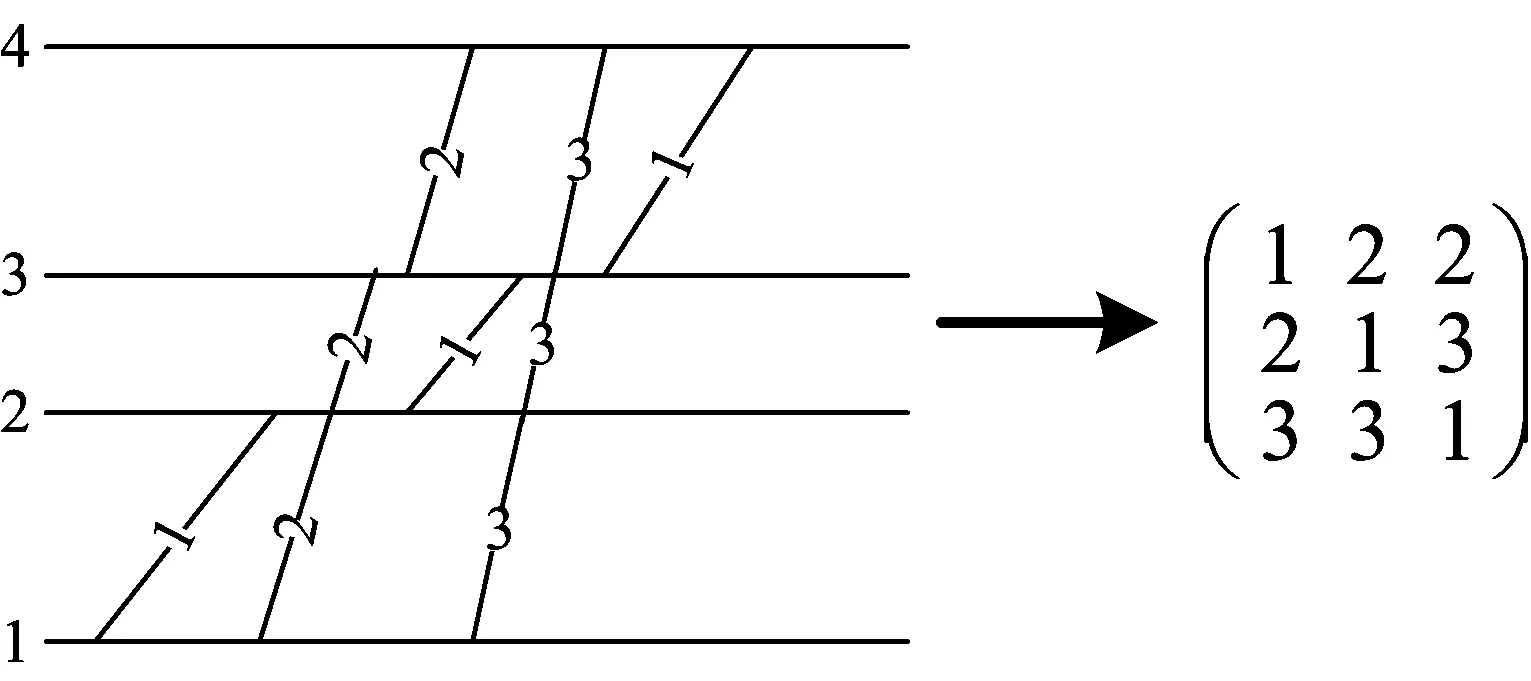
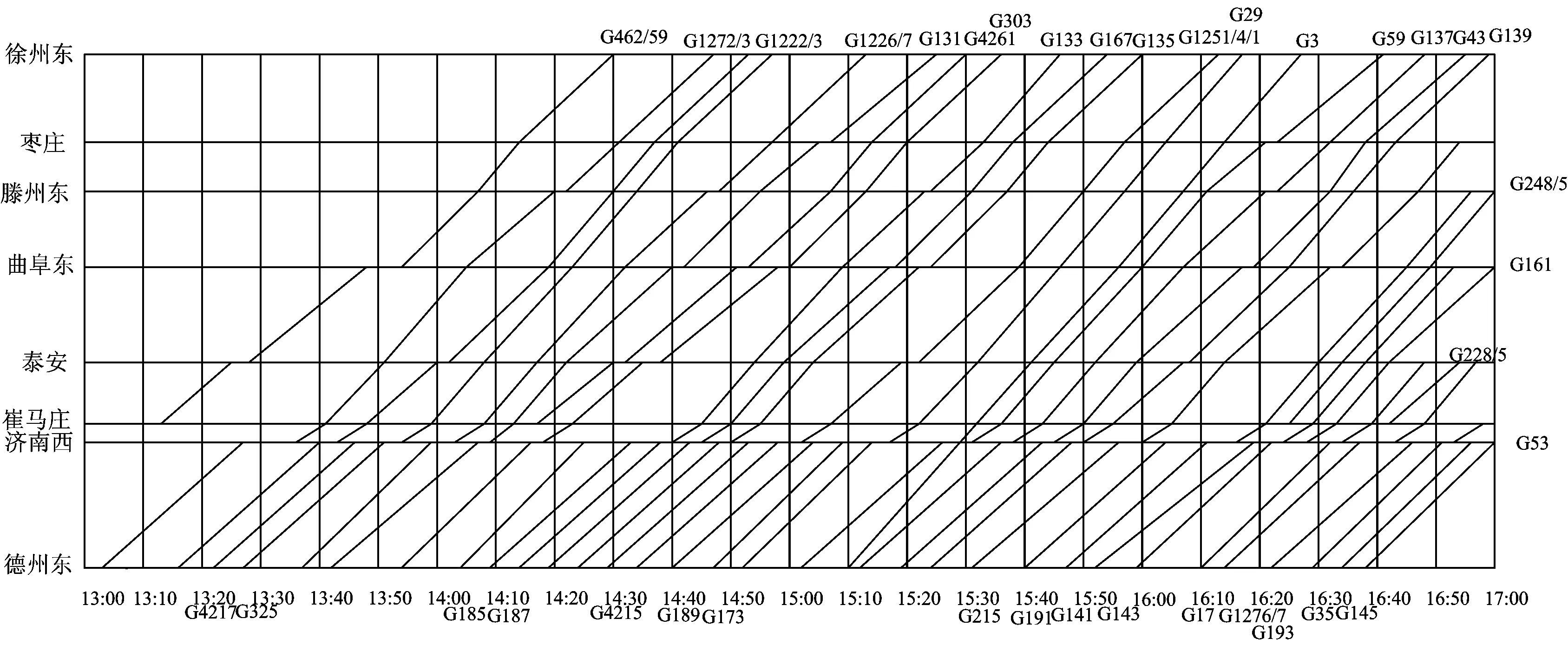
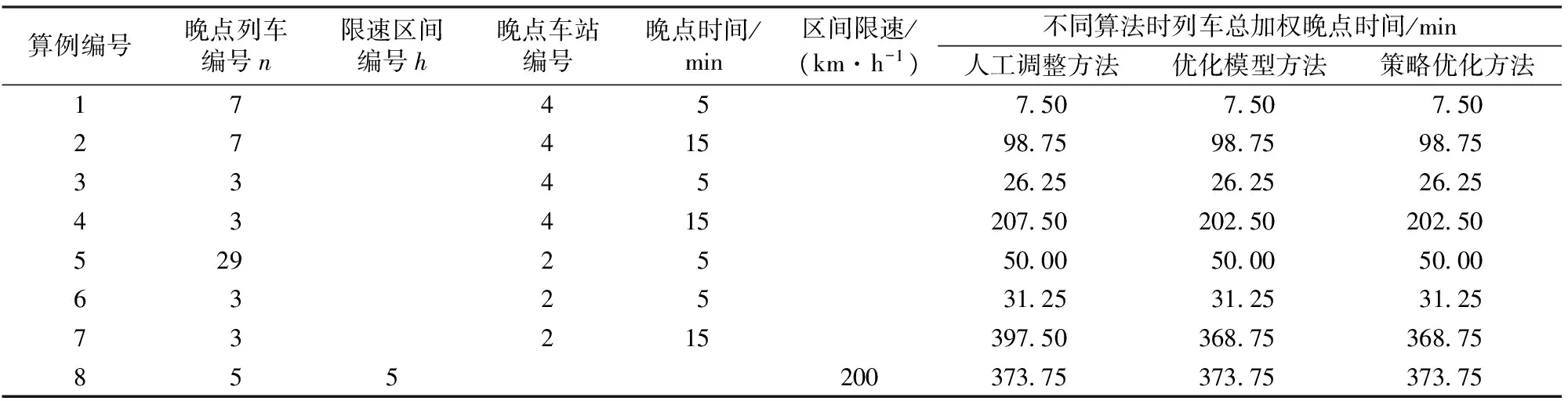
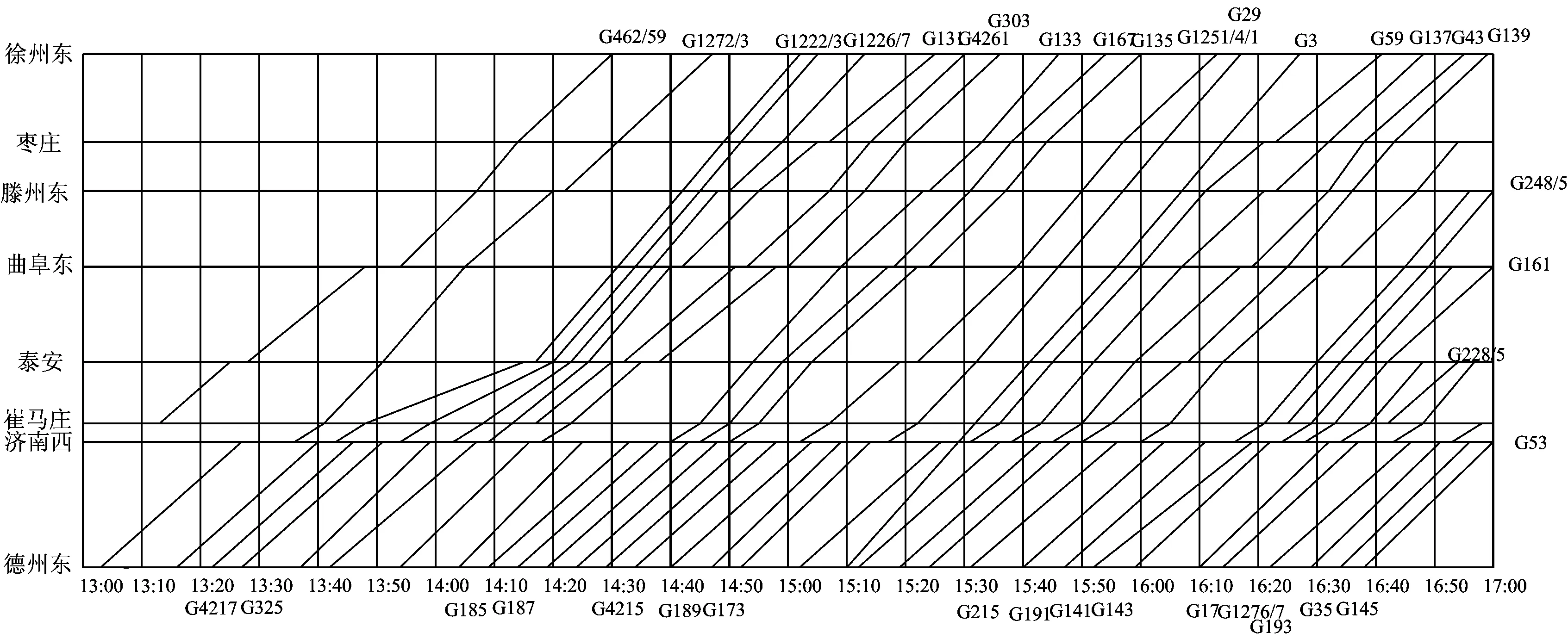
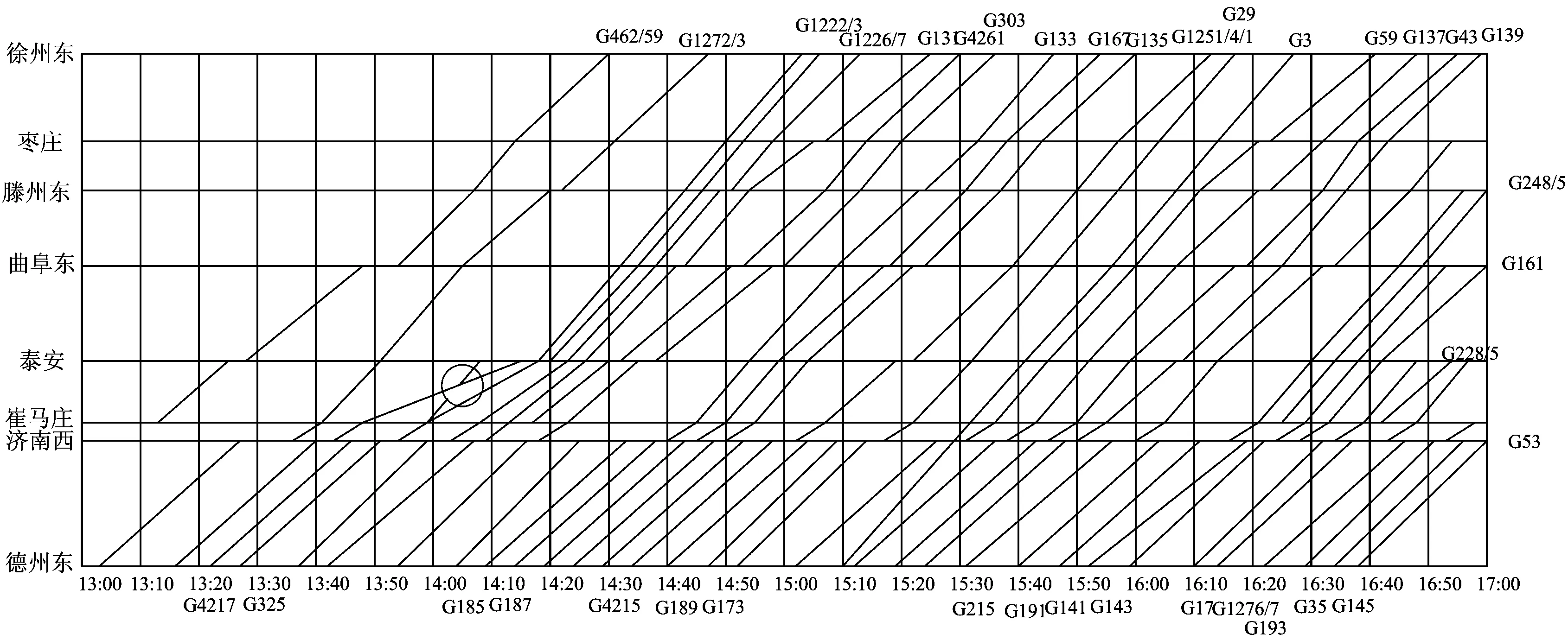
在决策时刻e,列车冲突状态ζe=3时,即中高速列车冲突,如图4所示。设t0为后行列车与前行列车在i站的预计到达时间之差;Iff为车站不同时发车最小间隔时间;ti和tj分别为列车i和列车j的区间运行时分,则有ti>tj(注:也可能前行列车为故障限速运行列车或严重晚点列车);li和lj分别为列车i和列车j的等级(或权重)。下面分t0 图4 状态ζ时列车冲突基本情况图 当t0 由图5可知,2种越行行动都可以疏解区间的冲突。分别计算2种越行行动下的报酬Tk和Tk+1,即列车i和列车j在区间内的加权总旅行时间(自在k站到达起直至从k+1站发车时止的时间),分别为 Tk=lj(tj+Idd-t0)+li(Idd+Iff+ti) (2) Tk+1=lj(ti+Idd-t0)+li(ti+Idd+Iff) (3) 图5 当t0 已知ti>tj,故Tk 同时,列车j无论是在k站越行还是在k+1站越行,列车i离开k+1站的时间相同,即对下一个状态的后行列车影响是相同的,则列车j在k站进行越行为最优行动。 当t0≥Idd时,列车在k站或k+1站的越行行动如图6所示。 图6 当t0≥Idd时列车在k站或k+1站的越行行动 由图6可知,与图5情况不同之处在于,若列车在k站越行,则只需调整列车i即可,列车j完全不受干扰。分别计算此时的Tk和Tk+1,即 Tk=ljtj+li(t0+Iff+ti) (4) Tk+1=lj(ti+Idd-t0)+li(ti+Idd+Iff) (5) 令Tk≤Tk+1,由式(4)和(5)可得 (6) 令Tk>Tk+1,由式(4)和式(5)可得 (7) 基于定理2和列车越行行动有如下推论。 推论:在高速铁路列车运行调整过程中,采取相应调整行动,使前后两相邻存在潜在冲突的列车其关系始终满足条件1或条件3,且在任意状态下采取的列车越行行动均为最优行动,即每个决策规则要求在每个可实现的历史都应采取列车越行行动,则这些行动对应的马氏决策策略是1个最优策略。 应该看到,在高速铁路行车调度决策过程中,如果采取相应调整行动,使前后两相邻存在潜在冲突的列车其关系满足条件2时,尽管其出现概率很小,但理论上并不能保证后续优化行动序列对应的策略为最优策略,此时,可以分别计算不同越行行动在前方站和后方站的报酬,采取多步的状态递归方法,再比较其优劣,从中选择更优化的行动序列。 3.1.1矩阵的建立 假定在调整时段内某个区段上有K个车站、N列列车,定义如下矩阵。 列车越行矩阵O=(oi,k)N×(K-1),矩阵元素oi,k为第i行第k列位置上的数据,取第k个运行区间内按时间顺序排在第i位的列车编号,i∈{1,…,N},k∈{1,…,K-1}。如图7所示:列车越行矩阵的第1列数据1,2,3分别对应第1个运行区间内按时间顺序的列车编号1,2,3;第2列数据2,1,3分别对应第2个运行区间内按时间顺序的列车编号2, 1, 3;可见,列车1和列车2的位置顺序交换了,这是因为在k=2站列车1被列车2越行;依次类推,可以得到整个区段中的列车越行矩阵。 列车i在k站的到、开时刻矩阵X=(xi,k)N×(2K-2),其中,xi,2k-1为列车i在k站的到达时刻,xi,2k为列车i在k站的出发时刻,k=1,2,…,K-1。 图7 区段内列车越行矩阵图示 3.1.2极大加代数法推算列车运行时刻表 采用文献[16]给出的基于极大加代数和矩阵的列车时刻表递推算法,可以快速推算在确定越行顺序和无冲突列车条件下,由状态ζe到状态ζe+1所有列车在不同车站的到发时刻。 (1)第1列车在其经过k站时的到发时刻x1,2k和x1,2k+1,以及各次列车按照最小发车间隔在始发站的始发时刻xi,1的计算式分别为 (8) k=2,…,K; xi,1=Iff(i-1);i=2,…,N (9) (2)后续列车在k站的到达时刻xoi,k,2k和发车时刻xoi,k+1,2k+1的计算式分别为 k=1,2,…,K-2;i=2,3,…,N (10) xoi-1,k+1,2k+1+Iff) k=1,2,…,K-2;i=2,3,…,N (11) (3)后续列车在终到站K的到达时刻xoi,K-1,2K-2的计算式为 (12) i=2,3,…,N (4)定义yi,K为列车i到达终点站K的图定终到时刻,所有列车的总加权晚点时间tall的计算式为 (13) 根据上文的理论和计算公式,设计的高速铁路列车运行调整策略优化方法步骤如下。 Step1:从调整初始时刻开始,按照基本图的越行矩阵,运用式(8)—式(11)计算各次列车(含初始晚点列车)在各站的到发时刻,并按照时间先后顺序,同步比较相邻列车在各站的到发时刻是否存在冲突,若存在冲突,则令e=0, 转Step2;否则转Step6。 Step2:对于系统状态ζe,根据冲突列车是否出现严重晚点或列车晚点是否超过最大可接受时间的情况,判断其是否符合2.2节给出的列车顺晚依次行动的最优策略条件,若符合则转Step3,否则转Step4。 Step3:采取顺晚行动疏解冲突状态ζe,列车越行矩阵保持不变,转Step5。 Step4:根据2.3节给出的列车越行行动的最优策略条件,采取相应越行行动疏解冲突状态ζe,同时修改列车越行矩阵。 Step5:按照新的列车越行矩阵,运用式(8)—式(11)计算各次列车在后续各站的到发时刻,并按照时间先后顺序,同步比较相邻列车在各站的到发时刻是否存在冲突。若存在新的相邻冲突列车,则令e=e+1,转Step2;否则转Step6。 Step6:计算所有列车的总加权晚点时间tall,输出结果,计算结束。 选取京沪高速铁路德州东至徐州东区段下行方向为例,该时段列车密度相对密集,前行列车出现晚点后对后续列车运行将产生较大影响。该区段共有8个车站,依次为德州东、济南西、崔马庄(线路所)、泰安、曲阜东、滕州东、枣庄、徐州东站,对应车站编号为k=1,2,…,8;调整时段选取某天的13:00—17:00;调整时段内基本列车运行图采用实际的运行图,如图8所示,列车按照进入该调整区段的时间先后编号为1~37(具体车次见图8);其中,区间运行时间、车站间隔时间、列车运行时刻表、列车停站情况可参见京沪高速铁路列车运行图资料[18]。 由于此次调整不存在中速列车,假定5号列车(G325)、12号列车(G133)、19号列车(G29)、21号列车(G3)、27号列车(G141)、35号列车(G35)这6列列车为重点列车,列车等级为2.5,其余列车等级为1.25。随机产生8个列车晚点算例,其中,第1—第7个算例对应于不同的单列列车晚点情形,第8个算例对应于由于天气异常需要临时限速,从而导致多列车晚点情形,且临时限速200 km·h-1;晚点列车编号n,限速区间编号h(对应车站h到车站h+1的区间,经过该区间的列车由于限速等原因假定均晚点一定时间)和晚点列车所在车站的编号均见表1。 图8 调整区段的基本列车运行图 分别采用人工调整、传统的优化模型方法和本文的策略优化方法进行列车运行调整,采用主频为2.5 GHz的联想Y480电脑计算,策略优化调整的平均时间约为5 s,而优化模型计算时间约为6 min,计算运行图调整方案的列车总加权晚点时间,结果也列于表1中。以算例4为例,对应列车3在车站4的晚点,列车晚点运行图人工调整方案如图9所示,采用本文的模型和策略优化方法调整得到的列车运行图如图10所示。由于采用了越行的调整方式(注:圆圈处为冲突列车位置),较人工方案加权晚点时间减少5 min。 由表1、图9和图10结果可以看出,表1最后2列数据完全相同,表明采用策略优化方法与传统数学模型的优化结果相同,且能取得较人工调整方法更好的优化效果,而较传统数学优化模型方法,又可大大提高问题的求解效率,这说明策略优化方法具有优良的计算性能,能满足高速铁路行车调度决策系统开发的需要。 表1 采用不同列车运行调整方法时不同算例的列车总加权晚点时间 图9 列车晚点运行图人工调整方案 图10 策略优化后的列车运行图 本文运用马氏决策过程模型和策略优化方法研究了高铁列车运行调整问题,通过设立相邻且存在冲突的列车所在的位置为状态,选择列车顺晚、前方站越行、后方站越行等调度员可采取的调整措施作为行动,采用列车加权总晚点时间作为行车调度员获得的报酬,构建了高速铁路列车运行调整问题的马氏决策过程模型;给出了列车顺晚开行和越行调整行动的最优策略条件。在此基础上,设计了策略优化方法。以某高速铁路区段为例,假设多种典型晚点情况进行调整,通过人工调整、传统数学模型优化方法与本文的策略优化方法的比较,表明策略优化方法能取得较人工调整方法更好的优化效果,较传统的数学模型优化方法可大大提高求解效率,从而验证了高速铁路列车运行调整马氏决策过程模型和策略优化方法的有效性,也为进一步深化研究列车运行调整的快速有效方法提供了解决问题的新途径。 [1]CORDEAU J, TOTH P, VIGO D. A Survey of Optimization Models for Train Routing and Scheduling[J]. Transportation Science,1998, 32 (4):380-404. [2]ANDREA D’Ariano,DARIO Pacciarelli,MARCO Pranzo. A Branch and Bound Algorithm for Scheduling Trains in a Railway Network[J]. European Journal of Operational Research,2007, 183 (2):643-657. [3]CAPRARA A,FISCHETTI M,TOTH P. Modeling and Solving the Train Timetabling Problem[J]. Operations Research,2002,50(5):851-861. [4]ZHOU Xuesong,ZHONG Ming. Bicriteria Train Scheduling for High-Speed Passenger Railroad Planning Applications[J]. European Journal of Operational Research, 2005,167(3):752-771. [5]王涛, 张琦; 赵宏涛, 等. 基于替代图的列车运行调整计划编制及优化方法[J]. 中国铁道科学,2013,34(5):126-133. (WANG Tao,ZHANG Qi,ZHAO Hongtao,et al. A Method for Generation and Optimization of Train Operation Adjustment Plan Based on Alternative Graph[J]. China Railway Science,2013,34(5):126-133. in Chinese) [6]KRASEMANN J T. Design of an Effective Algorithm for Fast Response to the Re-Scheduling of Railway Traffic during Disturbances[J].Transportation Research Part C,2012,20(1):62-78. [7]季学胜,孟令云.列车到发时刻与进路同步优化的高速铁路列车运行调整模型[J].中国铁道科学,2014,35(4) ): 117-123. (JI Xuesheng,MENG Lingyun. Train Operation Adjustment Model for Synchronously Optimizing Train Arrival/Departure Time and Route on High Speed Railway Network[J]. China Railway Science,2014,35(4): 117-123. in Chinese) [8]陈雍君,周磊山.基于序优化方法的列车运行调整算法研究[J].铁道学报,2010,32(3):1-8. (CHEN Yongjun,ZHOU Leishan. Study on Train Operation Adjustment Algorithm Based on Ordinal Optimization [J]. Journal of the China Railway Society,2010,32(3):1-8. in Chinese) [9]李晓娟,韩宝明,李得伟,等.基于转换极大代数和序优化的高速列车运行调整方法[J].中国铁道科学,2013,34(6):124-130. (LI Xiaojuan, HAN Baoming, LI Dewei,et al. Method for High-Speed Train Operation Adjustment Based on Switching Max-Plux-Linear System and Ordinal Optimization[J].China Railway Science, 2013,34(6):124-130. in Chinese) [10]董守清,王进勇,闫海峰. 双线铁路列车运行调整的禁忌搜索算法[J]. 中国铁道科学,2005,26(4):114-119. (DONG Shouqing,WANG Jinyong,YAN Haifeng. Tabu Search for Train Operation Adjustment on Double-Track Line[J]. China Railway Science,2005,26(4):114-119. in Chinese) [11]王宏刚,张琦,王建英,等. 基于遗传算法的高速铁路行车调整模型[J]. 中国铁道科学,2006,27(3):96-100. (WANG Honggang, ZHANG Qi, WANG Jianying, et al. GA-Based Model of Train Operation Adjustment forHigh-Speed Railway[J]. China Railway Science,2006,27(3):96-100. in Chinese) [12]WHITE D J. Markov Decision Processes[M]. Chichester:Wiley Press, 1993. [13]董泽清, 刘克. 无界报酬折扣半马氏模型最优策略的结构[J]. 中国科学:A辑,1985,15(11):975-985. (DONG Zeqing,LIU Ke. Structure of Optimal Policy for Semi Markov Model with Unbounded Reward and Discount [J]. Scientia Sinica:A Edition,1985,15(11):975-985. in Chinese) [14]石雨.客运专线列车运行调整的策略、模型与算法[D]. 北京: 北京交通大学,2010. (SHI Yu. Strategies Models and Algorithms of Train Operation Adjustment for the Passenger Dedicated Railway [D]. Beijing: Beijing Jiaotong University,2010. in Chinese) [15]BLACKWELL D. Discrete Dynamic Programming[J]. Annals of Mathematical Statistics,1962,33:719-726. [16]李传宾. 基于矩阵表示和极大代数法的高铁周期列车运行图编制方法研究[D]. 北京:北京交通大学,2012. (LI Chuanbin. Research on Periodic Timetabling for the Trains on High-Speed Railway Using Matrix Representation and Max-Plus Algebra Theory[D]. Beijing: Beijing Jiaotong University,2012. in Chinese) [17]端嘉盈.高速铁路开通后既有繁忙干线运能计算及分析方法研究[D].北京:北京交通大学,2013. (DUAN Jiaying. Research on the Carrying Capacity Calculation and Analysis Method of Existing Busy Main-Line after the High-Speed Railway Opened[D]. Beijing: Beijing Jiaotong University,2013. in Chinese) [18]中国铁路总公司.铁运函[2011]328号 关于公布京沪高速铁路列车运行图的通知[S].北京:中国铁路总公司,2016.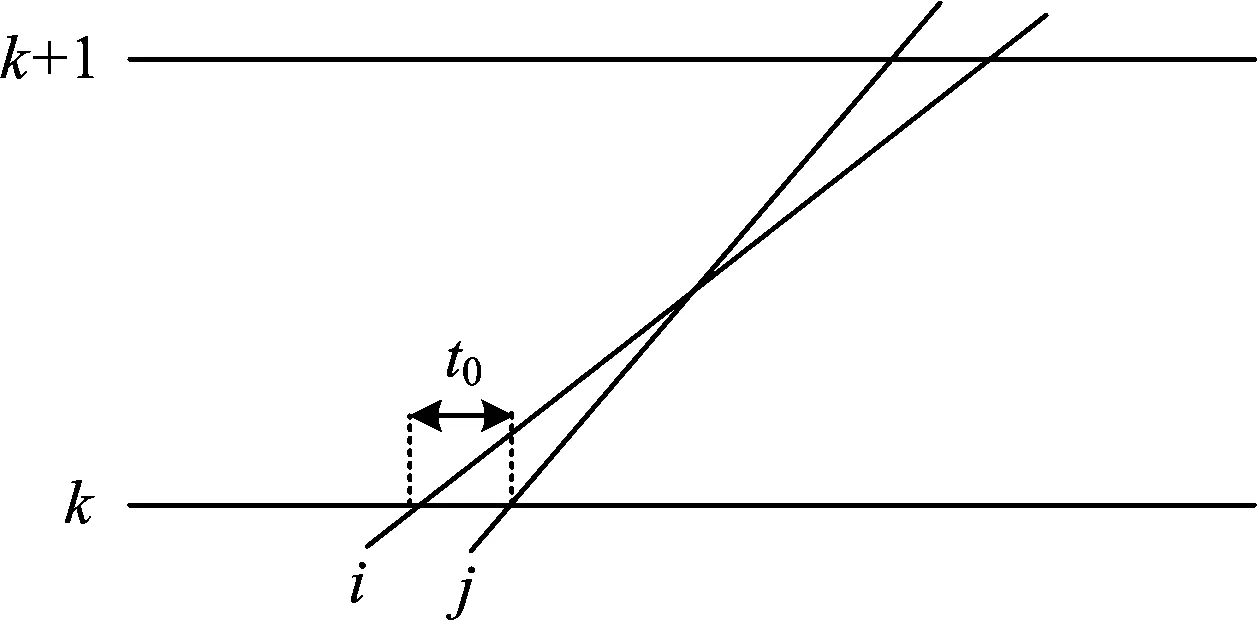
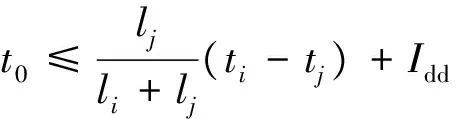
3 策略优化方法
3.1 基于极大加代数和矩阵的列车到发时刻计算方法[16-17]

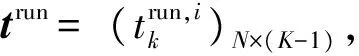
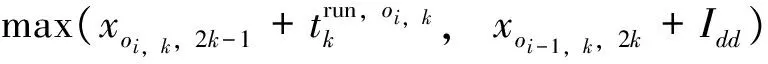
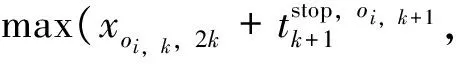
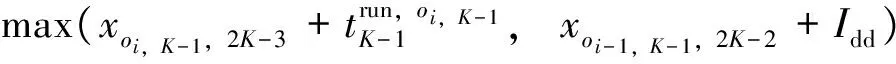
3.2 策略优化方法的实现
4 算例分析
4.1 实例概况
4.2 调整计算结果
5 结 论

