“边角”料的完美价值
—— 再论“SSA”
广东省佛山南海实验中学(528200) 刘锋
“边角”料的完美价值
—— 再论“SSA”
广东省佛山南海实验中学(528200) 刘锋
这是一个朴素而又不失乐趣的平面几何问题,我们甚至能不假思索地猜想到该问题相关的结论是什么,却又对所猜想的相关结论总有一丝疑惑.问题的解决,既用到几何画板直观验证,又用到代数知识推理论证,由浅入深,引人入胜.问题本身的内在美及其所承载的数学价值,值得我们静心感受.
1 引言
在现行的北师大版初中数学教材体系中,边边角(以下简称SSA)是在八年级下册第18页作为反例出现,说明“SSA”并不能确定三角形全等,而证明直角三角形全等有特殊方法“HL”.由此,会有部分学生有这样的惯性思考:如果两个三角形都是锐角三角形或者都是钝角三角形时,是否可以用“SSA”判断它们全等呢?
2 “SSA”适用性的初步讨论
为了系统、完整地阐述这一问题,我决定按以下两种方式进行分类讨论,一是按三角形本身进行分类,分为锐角三角形、直角三角形、钝角三角形进行讨论;二是按对应角(即“SSA”中的“A”)进行分类,分为对应角是锐角、对应角是直角、对应角是钝角进行讨论.
2.1 对三角形的分类讨论
若两个三角形是直角三角形,可以简单论证.
若两个三角形是锐角三角形:如图1,在锐角△ABC和锐角△A1B1C1中,AB=A1B1,AC=A1C1,∠B=∠B1,求证:△ABC~=△A1B1C1.

图1


若两个三角形是钝角三角形,则不能通过上述证明方法得到全等,那么是否可以找出反例说明“SSA”在两个钝角三角形中不适用呢?
借助几何画板,可以构造图2所示图形,在△ABC和△ABC1中,AB=5cm,AC= AC1=4cm,∠B=30°.经测量,∠CAC1=97.04°,∠BC1A=138.19°(精确到十分位).由此说明,“SSA”在两个钝角三角形中不适用.

图2
通过以上讨论,我们可以得出结论:
结论一:两边分别相等且其中一组对边的对角相等的两个直角三角形全等;
结论二:两边分别相等且其中一组对边的对角相等的两个锐角三角形全等;
结论三:两边分别相等且其中一组对边的对角相等的两个钝角三角形不一定全等.
2.2 对对应角的分类讨论
若对应角是直角,可以简单论证.
若对应角是钝角:
如图3,在钝角△ABC和钝角△A1B1C1中,AB= A1B1,AC=A1C1,∠B=∠B1,90°<∠B<180°, 90°<∠B1<180°,求证:△ABC~=△A1B1C1.
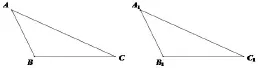
图3

若对应角是锐角,图2仍是一个很好的反例,说明对应角是锐角时,“SSA”不适用.
通过以上讨论,我们可以得出结论:
结论四:两边分别相等且其中一组对边的对角相等且对应角是直角的两个三角形全等;
结论五:两边分别相等且其中一组对边的对角相等且对应角是钝角的两个三角形全等;
结论六:两边分别相等且其中一组对边的对角相等且对应角是锐角的两个三角形不一定全等.
3 “SSA”不确定性的深入探讨
若我们的探讨就到此为止,未免平淡无味.以上两种分类方法,有一定的重合度,经过比较分析,我们可以进一步缩小“SSA”不适用的范围,得到以下结论:
结论七:两边分别相等且其中一组对边的对角相等且对应角是锐角的两个钝角三角形不一定全等.原因很简单,我们并不清楚另外一组相等的边所对的角是否相等,这组角可能相等,也可能互补.我们再进行以下的尝试:

根据以上论证可以得出以下结论:
结论八:两边分别相等且其中一组对边的对角相等且对应角是锐角的两个钝角三角形,若对应角所对的边不小于三角形中的最短边,则这两个三角形全等.
结论九:两边分别相等且其中一组对边的对角相等且对应角是锐角的两个钝角三角形,若对应角所对的边是三角形最短边,则这两个三角形不一定全等.
4 “SSA”的相关应用
在现行的教材中,“SSA”不能用来证明三角形全等,也没有对此做过多的论述,但这并不代表“SSA”没有用武之地.
例:同学们都知道,只有两边和一角对应相等的两个三角形不一定全等.你如何处理和安排这三个条件,使这两个三角形全等?比如:设有两边和一角对应相等的两个三角形,如果这组角的对边恰好都是这两边中较大的边,那么这两个三角形全等.请你仿照上例,再写出三个使这两个三角形全等的方案.
解析:可以有以下参考方案:
方案一:如果这个角是这两边的夹角,那么这两个三角形全等;
方案二:如果这个角是直角,那么这两个三角形全等;
方案三:如果这个角是钝角,那么这两个三角形全等;
方案四:如果这两个三角形都是锐角三角形,那么这两个三角形全等.
这是一道开放型的方案设计题,通过分析,可以知道在什么情况下“SSA”能判断两个三角形全等.
结论
行文至此,已近尾声.纵观现今初中数学教材的安排,“SSA”犹如沧海遗孤,很少被提及或是作为反例,未免有些遗憾.运用分类讨论思想,我们不难发现,从三角形的三条边、三个角中选取三个条件,应该有三个角(AAA)、两角一边、一边两角和三条边(SSS)四大类,两边一角分为边角边(SAS)和边边角(SSA),一边两角分为角边角(ASA)和角角边(AAS).因此,只有“SSA”的加入,才能使得这是一个完整的体系.而对“SSA”的研究和讨论,其过程远比其它几个判定三角形全等的定理或推论的获得更富有趣味性和思想性.而“SSA”本身,也体现了数学的完整美.
[1]黄国辉.全等三角形判定中的“边、边、角”问题探讨.抚州师专学报, 1985.
[2]陈德前.满足“SSA”的两个三角形全等吗?.中学生数理化(八年级数学)(配合人教社教材),2014.7-8.
[3]查萍伟.“SSA”与中考题.中学生数理化(八年级数学)(配合人教社教材),2015.7-8.

