最短路线之我见

甘肃省武威市凉州区武南镇九年制学校(733009) 徐辉章

最短路线之我见

甘肃省武威市凉州区武南镇九年制学校(733009) 徐辉章

在初中数学中,有一类问题是求按满足某些特定条件连结,使所连结的线段的长度之和最小,称之为最短路线.最短路线问题通常是以“两点之间,线段最短”为原则引申出来的,本文通过一些例子,介绍一些求最短路线问题的方法.

一、两点之间线段最短

我们知道,连结两点之间所有的线中,线段最短.将它扩展、延伸可得到一个最短路径问题、即求连接A、B两点的线段中哪一条最短.

当A、B在同一平面内时,即使是从乌鲁木齐到北京,我们也可以轻松地利用“两点之间,线段最短”得出线段AB是A、B两点间的最短路径(如图1).

图1

二、饮马问题

如图2,A为马厩,B为草地,L为一条河流,牧马人某一天要从马厩牵出马,先到河边饮马,再到草地牧马,请你帮他确定这一天的最短路线.

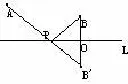
图2

已知:如图2,直线l及点A、B.

求作:点C在直线l上,AP+BP最小.

作法:1.作B关于直线l的对称点B′连接AB′交l于点P连接AP路线A−P−B就是最短路线

证明:略

三、蚂蚁爬行路线最短问题

1.正方体、长方体

如图4,一只蚂蚁要从正方体的一个顶点A′沿表面爬行到顶点C,怎样爬行路线最短?

图3

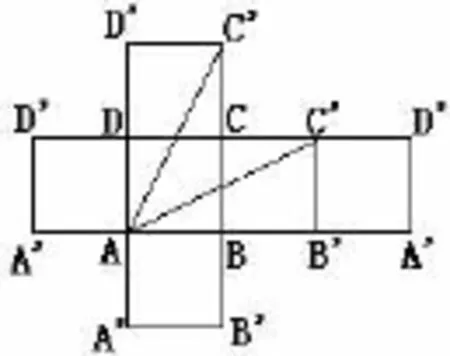
图4

分析:求点A′到点C的最短路径是那一条.此时已不在同一平面内,不能直接利用公理解决问题.此时,就要利用数学中的转化思想,把立体图形转化成平面图形来研究(如图4).

从而得到两条最短路径:A→BC→C′和A→CD→C′.长方体最短路线问题与正方体类似,这里就不详细说明了.

2.圆柱体

如图5所示是一个底面半径为3,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一圈到达B点,求蚂蚁爬行的最短路程.

图5

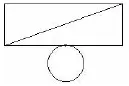
图6

把圆柱体展开(如图6),此时,只有AB才是最短路径,且只有一条最短路径.

3.圆锥问题

如图7所示是一个底面半径为三分之二,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短距离.

分析:先求得的侧面展开图扇形的中心角是60度;于是需求的线段AA′是等边三角形的边长,蚂蚁爬行的最短路程是4.

图7

四、三角形周长问题

A是锐角MON内部任意一点,在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小.(如图所示)