源于课本题的一道高考题的多种解法

江苏省南京市金陵中学(210005) 祁云

源于课本题的一道高考题的多种解法

江苏省南京市金陵中学(210005) 祁云

三角变换是历年高考的必考考点之一,也是要求学生熟练掌握和运用的知识点.以2016年江苏高考数学填空题的第14题为例,题目将三角变换和不等式结合,有一定的难度:

14.在锐角三角形ABC中,sinA=2sinB sinC,则tanAtanB tanC的最小值是____.

【答案】8.

【解析】注意到题中条件两边的次数不齐,考虑将sinA改写为sin(B+C),得sinB cosC+cosB sinC= 2sinB sinC.锐角△ABC中,cosB＞0,cosC＞0.在上式的两侧同时除以cosB cosC,得tanB+tanC=2tanB tanC.此时,条件中仅剩下B与C的关系,于是将所求式也化为仅和B、C相关.因为

点评:这两种方法都采用了“消元”的思想.先利用A+B+C=π将三个变量转化为两个变量B、C,然后方法二是令t=tanB tanC再转化为一个变量,方法三是令t=tanB+tanC再转化为一个变量.难点在于第二步,即如何实现变量形式的统一化.

点评:多元问题除了一元化之外,还可以直接运用基本不等式求得最值.

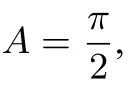
数学必修2第103页习题10“已知M(x,y)与两个定点O(0,0),A(3,0)的距离之比为那么点的坐标应满足什么关系?”

数学选修2-1第51页例2“求平面内到两个定点A,B的距离之比等于2的动点M的轨迹轨迹方程.”的综合改编.

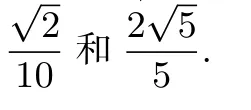
(1)求tan(α+β)的值;

图1

(2)求α+2β的值.

18.在平面直角坐标系xOy中,二次函数f(x)= x2+2x+b(x∈R)与两坐标轴有三个交点.记过三个交点的圆为圆C.

(1)求实数b的取值范围;

(2)求圆C的方程;

(3)圆C是否经过定点(与b的取值无关)?证明你的结论.

数学必修2第101页例3“已知△ABC的顶点A(4,3),B(5,2),C(1,0),求△ABC外接圆的方程.”数学必修2第80页第8题“设直线y−3=k(x+2).当k取任意的实数时,这样的直线应具有什么共同特点?”的综合改编.

所以我们在高三这一年的综合复习中,不能仅仅局限于大量的题海中,而是要着眼于课本,回归教材,将例题习题真正理解透彻,才能以不变应万变,掌控高考的变化.