例谈初中数学有关三角函数应用题的四个模型

南雄市第二中学(512400) 黄端鑫

例谈初中数学有关三角函数应用题的四个模型

南雄市第二中学(512400) 黄端鑫

三角函数在初中是一个非常重要的函数,用途很广泛,我们常遇见直角三角形中三边的关系用勾股定理,而要联系角和边就需要借助三角函数,因此透过三角函数的定义和本身的意义的考查确实是监测学生各方面的知识和能力的好方法.尤其是有关三角函数应用题在中考试题中时常出现,做好此类应用题的解题环节是学生取得好成绩的关键所在.我认为一是加强三角函数基础知识的训练,二是要熟练掌握三角函数知识应用四个方面的知识模型,这样一定能做好三角函数应用的考题的,现举例分析说明.

图1

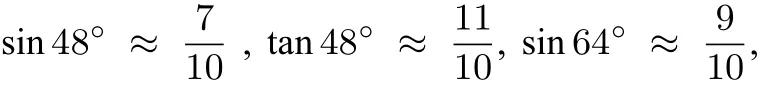
分析Rt△ADB中用AB表示出BD、Rt△ACB中用AB表示出BC,根据CD=BC−BD可得关于AB的方程,解方程可得.

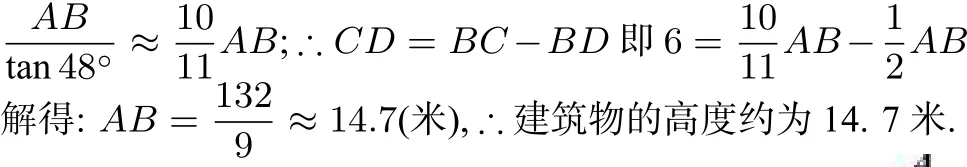
点评此题考查了解直角三角形的应用-仰角问题,主要是三角函数的基本概念及运算,关键是用数学知识解决实际问题.我们将这种图形归纳为一个模型(图2)

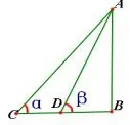
图2

例2(2015•韶关模拟)如图3,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=45°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.

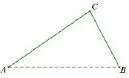
图3

(1)求改直后的公路AB的长;

(2)问公路改直后该路程比原来缩短了多少千米?(精确到0.1)

分析(1)过点C作CD⊥AB与D,根据AC=10千米,∠CAB=25°,求出CD、AD,根据∠CBA=25°,求出BD、BC,最后根据AB=AD+BD列式计算即可,(2)根据AC=10千米,BC=5.9千米,即可得出公路改直后该段路程比原来缩短的路程.

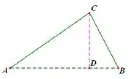
图4

对于第(1)小题的解答是:如图4,过点C作CD⊥AB与D,因为AC=10千米,∠CAB=25°,所以CD=sin∠CAB·AC= sin25°×10≈0.42×10=4.2 (千米),AD=cos∠CAB·AC=cos25°×10≈0.91×10= 9.1(千米),因为∠CBA=25°,所以BD=CD=4.2(千米),所以AB=AD+BD=9.1+4.2=13.3(千米).

点评本小题考查了解直角三角形的应用,用到的知识点是三角函数、特殊角的三角函数值,关键是作出辅助线,构造直角三角形,我们将这种图形归纳为一个模型(图5)

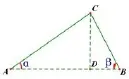
图5

例3(2016•云南昆明)如图6,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:

图6

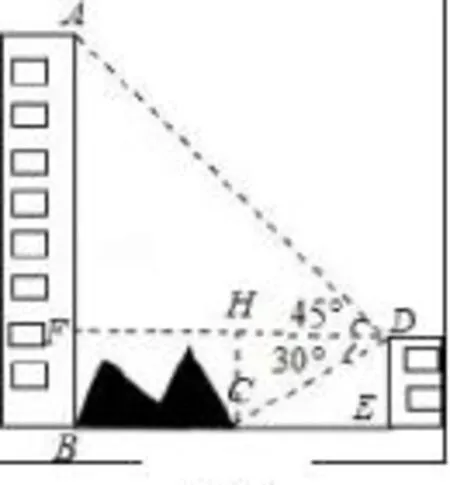
图7

点评此题考查了解直角三角形的应用-仰角俯角问题,主要是三角函数的基本概念及运算,关键是用数学知识解决实际问题.我们将这种图形归纳为一个模型(图8)

图8

例4(2016•湖北黄石)如图9,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,∠CBE=45°.

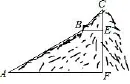
图9

(1)求AB段山坡的高度EF;

分析(1)作BH⊥AF于H,在Rt△AHB中根据正弦的定义可计算出BH的长,从而得到EF的长;(2)先在Rt△CEB中利用∠CBE的正弦计算出CE,然后计算CE和EF的和即可.

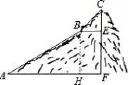
图10

点评此题考查了解直角三角形的应用-坡度与坡角问题:坡度是坡面的铅直高度和h水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=h:l的形式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=tanα.我们将这种图形归纳为一个模型(图11)

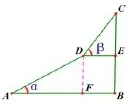
图11

总之,在求解有关三角函数背景下的应用题时,数形结合,借助三角函数,通过利用三角函数的定义和本身的意义,联系角和边的关系,进而解决实际问题.只要掌握了上面4个模型,反复训练,是很容易做好三角函数应用的考题的.

[1]《数学九年级教材下册》[M],人民教育出版社,2013;

[2]黄李珍,锐角三角函数的应用分类例谈[J],《数学学习与研究》, 2012,(14).