坡角对双坡屋盖风荷载特性影响分析

王 程，李方慧，张 杰，向本军，苏政忠

(黑龙江大学 a.水利电力学院；b.建筑工程学院，哈尔滨 150080)

0 引 言

近年来，双坡屋盖房屋材料朝着轻质高强方向发展，且房屋体型与屋面形式多变，其风荷载特性为建筑抗风设计所考虑的重要因素。历次风灾害调查报告显示，屋面破坏是低矮房屋破坏的主要形式之一[1]，而影响低矮房屋屋面风荷载的因素有很多，如房屋高宽比、屋面坡度、檐口大小等，其中屋面坡度是影响双坡低矮屋面风压的重要因素，且不同坡度对风压分布影响比较复杂，在实际房屋设计中难以确定最优的坡度方案。研究不同坡角作用下屋面风压分布特性可为实际工程设计提供理论依据。

国内外对双坡低矮建筑风压的研究方法主要分为实地观测、风洞实验、数值模拟。Hoxey R P等[2]、李秋胜等[3]、王旭等[4-5]多位国内外专家通过建立足尺模型研究了高度、宽度等参数对建筑屋面风压分布的影响，真实有效地总结出建筑风压分布特性，但实测所消耗的时间和财力也是巨大的，随后罗颖等[6]、高阳等[7]、Chen B等[8]、Hatem A等[9]通过建立缩尺模型，并进行风洞试验研究了多因素影响下的建筑风压分布以及屋面风压极值的检测。而随着计算机技术的进步和CFD数值模拟技术的不断成熟，对建筑抗风的研究方法就不局限于实测与风洞试验，黄强[10]通过对比TTU模型数值模拟的结果与风洞实验的结果，确定要使用的湍流模型和一些参数的设置，对低矮双坡屋面房屋模拟，总结出坡角、檐口和挑檐对平均风压系数的影响。戴成元等[11]通过对比分析RNGk-ε、SST、Realizablek-ε和Standardk-ε湍流模型的结果，分析了RANS模型与分离涡模型在模拟流场的湍流分布及结构背风处涡旋的分离脱落情况时的差距。杨庆山等[12]采用CDRFG (Consistent discretizing random flow generation)人工合成湍流方法生成大气边界层湍流,研究了来流湍流度对低矮建筑表面的平均、脉动以及极小值风压分布以及风压非高斯特性的影响。夏少军[13]采用数值模拟总结出不同山体布置形式对低矮房屋屋面风压分布的规律。而作为对建筑屋面风压分布初步研究，并能在短时间内经济、有效地得出结论，二维模拟不失为一种更优的选择。

因此，本文采用Realizablek-ε湍流模型在雷诺数为20 000的均匀流场中对二维典型双坡屋盖进行平均风压分布的数值模拟。分析了不同坡角下屋面平均风压系数的变化规律，并通过计算气动力系数以及结合流场变化机理确定湍流的形成与脱落的位置，从而得出屋面风压分布最不利位置以及对屋面风压分布影响关键的坡角，为此类建筑抗风措施提供建议。

1 数值模拟和计算模型

1.1 控制方程

文献[14]指出，当时均应变率很大时，Standardk-ε模型可能产生负的正应力。为了使流动符合湍流的物理定律，必须给正应力施加某种约束。其认为要实现这种约束，湍动黏度计算公式中的系数Cμ应该与应变率相关联，而不能认定为常数。于是，便提出了Realizablek-ε模型。该模型中k和ε的输运方程为

(1)

(2)

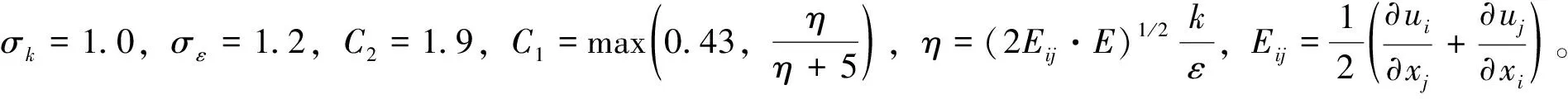
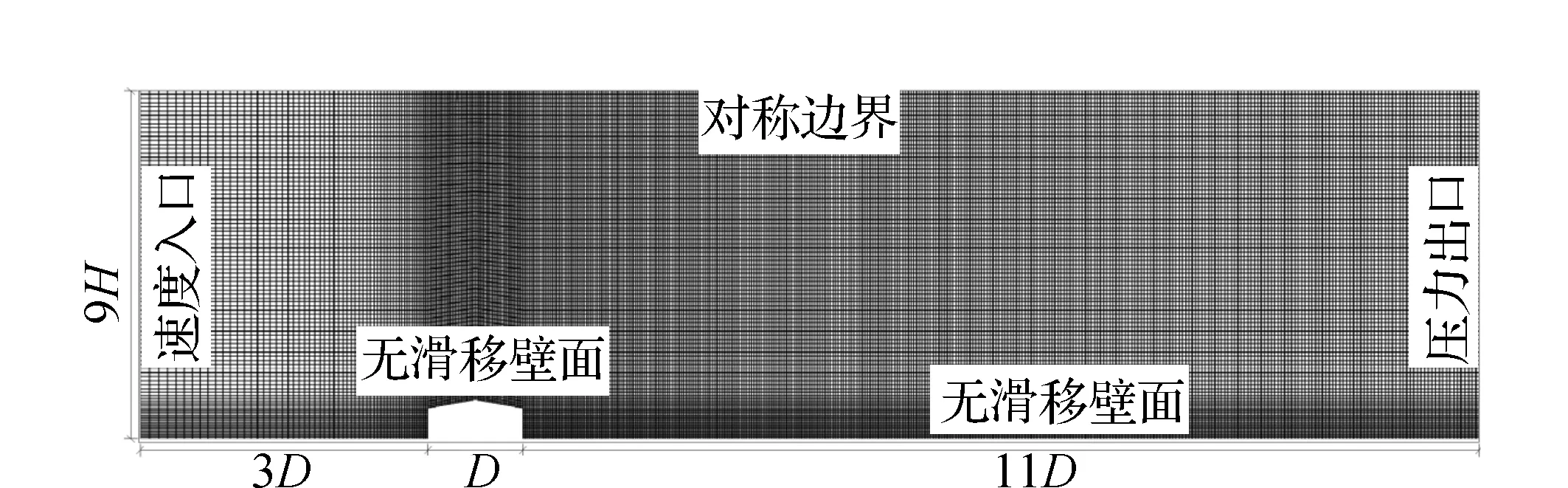
图1 计算模型、边界条件及计算域整体网格Fig.1 Calculation model, boundary conditions and theentire grid of the computational domain

1.2 计算模型与网格

本文计算模型见图1，房屋檐口高度h=0.414，长度D=1.293，屋脊高度H=0.528，其计算域取一长方形，其在模型前流场、后流场和高度的尺寸分别取为3.88、14.223和4.71。计算域的网格采用结构化网格，为了更精确地监测模型表面的参数，对模型边缘区域进行了局部加密，最小网格高度为0.027，对应y+<30。

计算域入口采用速度入口边界条件，来流风速采用沿高度不变的均匀流，上表面采用对称边界条件，下表面采用无滑移壁面，压力速度耦合方法采用SIMPLEC算法，残差收敛值设为1×10-3。

2 计算结果分析与讨论2.1 计算结果验证

为了验证计算结果的准确性，提取屋面风压系数模拟结果并与风洞实验结果[2]以及三维模拟结果[15]进行对比分析，见图2。本文模拟结果在迎风面屋檐处略大于风洞试验和三维模拟结果，这是由于二维模型迎风面为一条直线直接受风荷载作用，而三维模型受中线两侧的屋面湍流干扰影响，类似结构整体稳定性分析也同样具有复杂性[16]。屋脊处风压系数出现大幅度转折要早于风洞实验，其主要原因是屋脊为高流速区域，流场分离情况较强烈，湍流模型无法精确计算该位置湍流分流及回流的量。背风屋面受流场直接作用较小，其与实验结果相差不到10%。由此可见，采用二维模拟方法可有效反映屋面中线风压分布情况，从而说明本文模拟方法及参数设置的合理性。

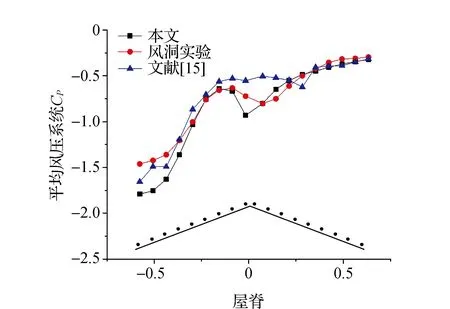
图2 10°屋面平均风压系数比较Fig.2 Comparison ofmean wind pressure coefficient on 10° roof

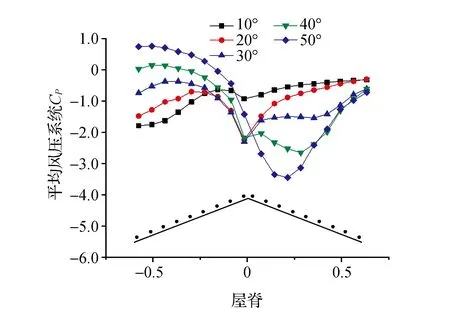
图3 坡角变化下屋面平均风压系数对比Fig.3 Comparison of roofmean wind pressure coefficient under slope angle change

2.2 坡角变化对平均风压系数的影响

坡角变化下屋面上方测点平均风压系数的变化见图3。屋盖迎风面平均风压系数随着坡角的增大而增大，坡角小于30°的屋盖迎风面风压系数皆为负值，而坡角大于30°的平均风压系数在屋檐处为正，在靠近屋脊处又转为负值。屋盖背风面平均风压系数皆为负值，随着坡角的增大，其平均风压系数也在增大。坡角小于30°时，越靠近屋檐其平均风压系数越小，在坡角为30°时背风屋面CP峰值为-1.6，而在50°坡角时背风屋面CP峰值为-3.6，相比30°坡角，50°坡角背风面CP增涨了1.31倍，坡角大于30°时，随着坡角的增大，背风面离屋脊0.25D处的风压增势急剧，该处风压增加约50%/10°，所以该位置为屋面风压最不利区域，而30°坡角是影响双坡屋盖前后屋面风压变化的转折点。

2.3 坡角变化对气动力系数的影响

为便于分析，对建筑的升力和阻力均进行了无量纲化处理，即：

(3)

(4)

式中：CL、CD分别为升力和阻力系数；ρ为空气密度；U0为来流风速；FL、FD分别为升力和阻力；D为房屋宽度；H为屋顶高度。下文分析中，CL,RMS为升力系数根方差值，CD,mean为阻力系数均值，分别表示脉动升力系数和平均阻力系数。10°～50°坡角下房屋的气动力系数见表1。通过对比不同坡角下升力系数和阻力系数的变化可得：当坡角小于30°时，平均阻力系数随着坡角的增大而减小，当坡角大于30°时，随坡角的增大而增大。平均升力系数随着坡角的增大而减小，脉动阻力系数受坡度变化的影响不大，脉动升力系数随着坡度的增大而增大。

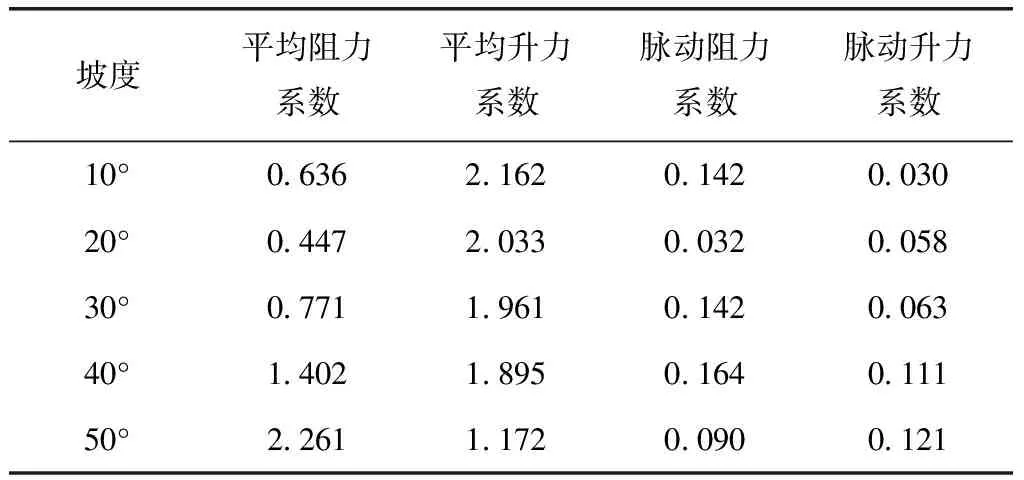
表1 气动力系数变化

2.4 流场分析

屋面受风压和风吸影响最显著的位置在近屋脊处，结合房屋周围及屋面流场涡结构详细分析风荷载作用机理以及从流场变化的角度验证30°为影响屋面风压分布的关键角度。10°～60°坡角房屋周围风速云图见图4，坡角变化对建筑屋面及周围的涡形成的位置、大小、形态均产生了明显的变化：在低坡角屋面，由于建筑立面的阻挡，屋顶迎风近壁面形成了低压甚至负压区，而随着坡角的增大，低负压区逐渐向背风面转移。屋顶背风近壁面随着坡角的增大，在30°坡角时产生负压漩涡，并且随着坡角继续增大，漩涡的尺寸与流场速度也在不断增大。在建筑前后区域流场中，坡角小于等于30°的房屋后流场中距建筑背立面0.2D位置有小型的漩涡产生，且其随着坡角的增大而增大。当坡角继续增加到30°以上时，建筑后流场漩涡消失。不同坡角屋面流线图见图5。在坡角小于等于30°建筑前流场中，建筑与地面夹角处有小型漩涡产生，而在坡角大于30°时，建筑前流场漩涡消失，建筑后流场漩涡随着坡角的增大慢慢向背风屋面转移，并且在50°时完全转移，在60°时漩涡达到最大。

图4 不同坡角屋面速度云图Fig.4 Cloud diagram of roof velocity at different slope angles

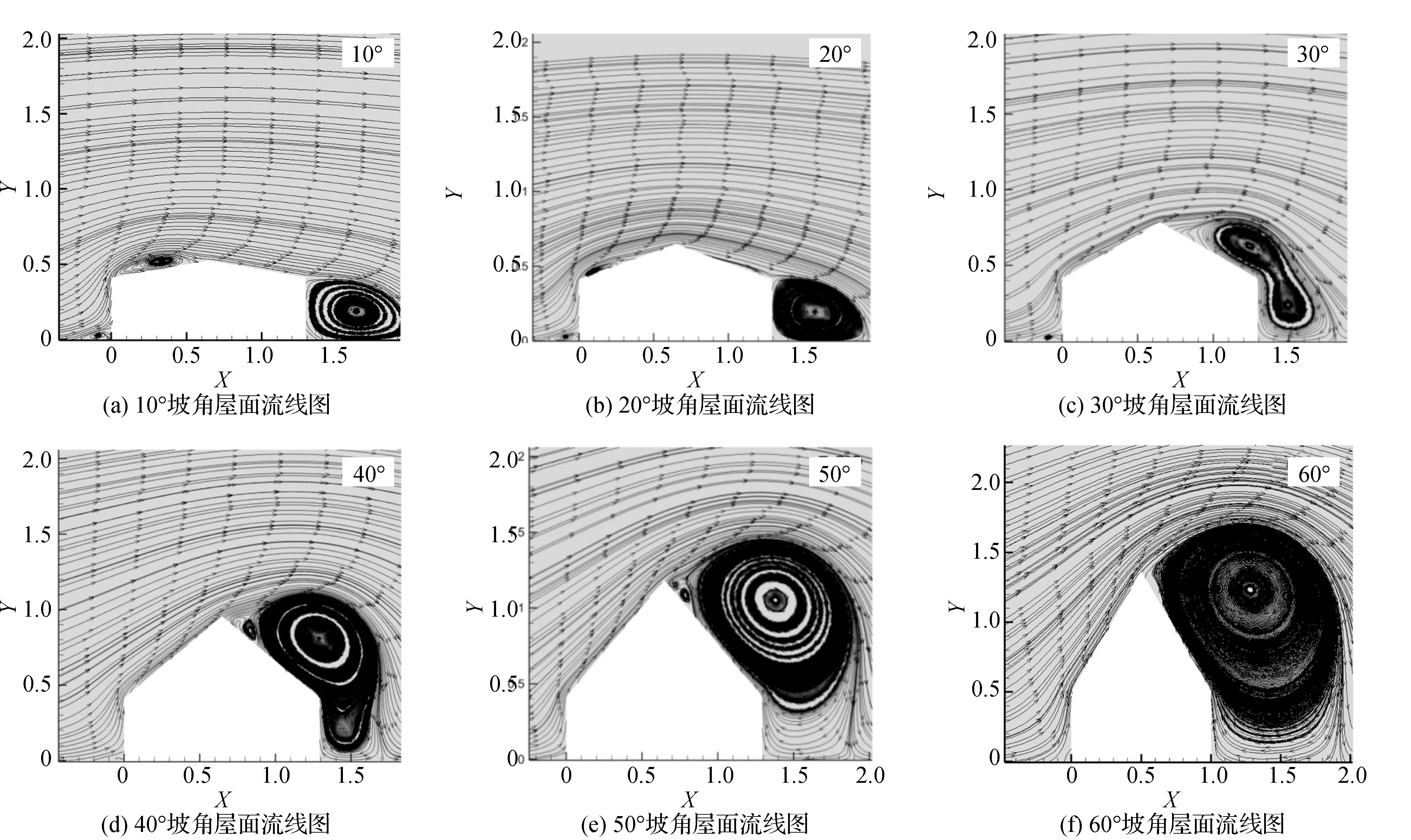
图5 不同坡角屋面流线图Fig.5 Stream diagram of the roof at different slope angles

3 结 论

通过Reynolds时均法，在雷诺数为20 000，均匀流场中对不同坡角房屋进行模拟，分析了随屋面坡角变化，屋面平均风压系数及气动力系数的变化规律，并从流场机理的角度验证了所得的规律，结论如下：

1)在均匀流场中，屋面平均风压系数随屋面坡角的增大而增大，且在坡角在30°以上屋面增速尤为明显，在坡角大于等于30°时，背风屋面离屋脊0.25D处平均风压系数产生突增，在坡角为30°时背风屋面平均风压系数峰值为-1.6，而在50°坡角时背风屋面平均风压系数峰值为-3.6，即30°～50°间背风面离屋脊2.5D处CP增涨了1.31倍，则该处为屋面风压最不利位置。

2)当坡角小于30°时，平均阻力系数随着坡角的增大而减小，当坡角大于30°时，随坡角的增大而增大。平均升力系数随着坡角的增大而减小，脉动阻力系数受坡度变化的影响不大，脉动升力系数随着坡度的增大而增大。

3)在坡角小于等于30°建筑前流场中，建筑与地面夹角处有小型漩涡产生，而在坡角大于30°时，建筑前流场漩涡消失，建筑后流场漩涡随着坡角的增大慢慢向背风屋面转移，并且在50°时完全转移，在60°时漩涡达到最大。

4)在低坡角屋面，由于建筑立面的阻挡，屋顶迎风近壁面形成了低压甚至负压区，而随着坡角的增大，低负压区逐渐向背风面转移。屋顶背风近壁面随着坡角的增大，在30°坡角时产生负压漩涡，并且随着坡角继续增大，漩涡的尺寸与流场速度也在不断增大。