巧分真假,“戏耍”增根

四川成都棠湖外国语学校(610225) 杨伟 刘佳

巧分真假,“戏耍”增根

四川成都棠湖外国语学校(610225) 杨伟 刘佳

我们知道分式方程的根有真根和假根(增根)之分,但你可知道增根中也有真假之分吗?

为此我们先来回顾一下增根的定义.

增根,是指在分式方程化为整式方程的过程中,若整式方程的根使最简公分母为0,(根使整式方程成立,而在分式方程中分母为0)那么这个根叫做原分式方程的增根.

从定义中我们可以很清楚的知道增根首先是分式方程化成的整式方程的根,这是前提,然后还要使分式方程的分母为0.只有同时满足这两个条件才能叫分式方程的增根.

下面我们就一起走进分式方程增根的世界,去感悟增根的真与假.

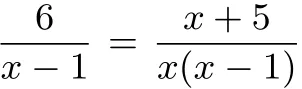
分析:此题是填空题,很多同学看完题目后会不加思索的填0或1,得出这样的答案源于学生对增根概念片面的理解:学生只注意了使分式方程分母为0,但忽略了“增根是把分式方程化成的整式方程的根”这一点前提要求.其正确解答如下:

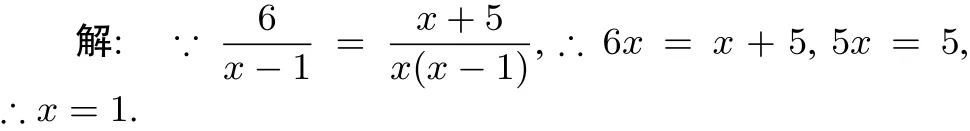
经检验,x=1是原方程的增根.故原方程的增根为x=1.

通过以上解答我们发现0根本就不是这个分式方程化成的整式方程的根,所以0当然也不是这个分式方式方程的增根,我们来看下面这个变式.

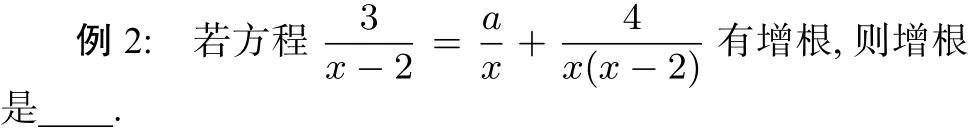
分析:此题是含有参数的分式方程,解答应先将参数看成已知数,把分式方程化为整式分程,再把可能的增根带入计算.

情况1:当x=2时,方程为6−2a=4−2a,明显此整式方程是无解的;故x=2不可能是原分式方程的增根.

情况2:当x=0时,方程为0=4−2a,∴a=2;此时x=0即为原分式方程的增根.

综上所述,原分式方程的增根为x=0.

很明显,如果只满足“分式方程化成的整式方程的根”这个前提条件也是不行的,我们来看下面的探讨:

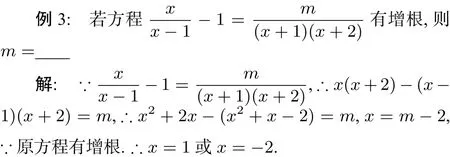
情况1:当x=1时,m=3;

情况2:当x=−2时,m=0;

增根的世界很精彩,我们在对增根这部分内容进行学习时一定要抓住概念,辨清概念后才能使在解题时有抓手,不出错,才能把知识掌握牢固.