“面积法”引入中学几何课堂

广州大学计算机科学与教育软件学院(510006) 廖红丽

“面积法”引入中学几何课堂

广州大学计算机科学与教育软件学院(510006) 廖红丽

平面几何是初中数学知识内容中的一个重要组成部分,也是初中数学教学中的一个难点,几何难学已是不争的事实.为了解决这个问题,很多数学教育家前赴后继地研究新的几何学习方法、教学方法,但仍无多大改观.有的数学教育家甚至提出要削减平面几何的在初中课本中的分量,这是不可取的.几何是数学学科的一个重要的知识模块,对培养学生的数学推理能力和严谨性思维有着不可替代的作用.两千多年来,中学几何课堂一直采用欧几里得的几何体系进行几何教学,公理、定理较多,解题的技巧比较灵活多变.张院士发现欧几里得几何仍然停留在“一题一法”的水平上,并没有一套强有力的通用的解题方法,使得学习几何的人觉得十分吃力[]1.如何去改良平面几何,处理好中学课本中的几何,已成为中学数学教学改革争论的焦点之一.

《义务教育数学课程标准(2011年版)》中指出,要培养学生几何直观能力,几何直观通俗上讲是借助直观的几何图形去思考复杂的问题,把问题简单化.在平面几何中,图形的面积无疑是最直观的.用“面积法”解题体现了数形结合的思想,除了在几何中可用“面积法”解题,在代数中“面积法”也非常实用.恒等式、不等式的证明都可以用“面积法”来证明,而且比用代数方法证明更加直观、简单.在初中平面几何中引入“面积法”的解题思想,并把面积作为解题的主线,改造初中几何,会不会是个好的改革方案呢?首先来学习两个基本定理——共边比例定理和共角比例定理.这两个定理易于掌握,而且非常实用,通过面积的关系转化为相应线段的关系可以把几何问题用代数方法解决,能解决很多比较难证的平面几何题.

首先引入两个基本概念——共边三角形和共角三角形.

定义1有一条公共边的两个三角形称为共边三角形.例如,如图1中,△ABC与△ABE,△BCD与△BCA,△ABD与△ADC,△ABD与△BDC等.

定义2有一组角对应相等或互补的两个三角形称为共角三角形.如图1中,△ABE与△CDE,△BCD与△BCA,△ABD与△ADC,△ABD与△BDC等.

为了书写简单,我们约定△ABC的面积S△ABC以后仍用△ABC表示.这里我们引入一个基本命题,由这个基本命题可以得到共边比例定理和共角比例定理.

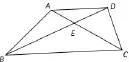
图1

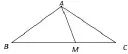
图2

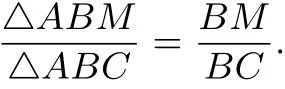
共边比例定理[]2有公共边的两个三角形面积之比等于它们第三顶点连线被公共边所截对应线段之比.上述共边比例定理可表示成:

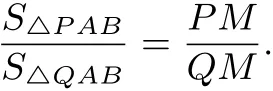
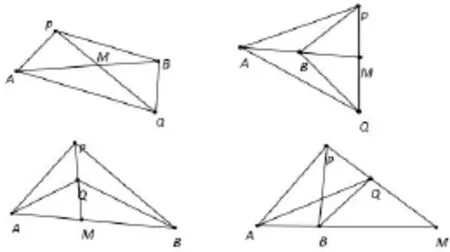
图3

共角比例定理[]2共角三角形的面积之比等于相等角或互补角的两夹边乘积之比.反之,若两个三角形的面积之比等于对应角两夹边乘积之比,则两角相等或互补.上述定理可写成:

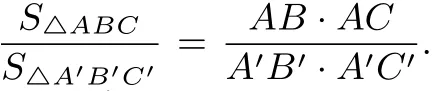
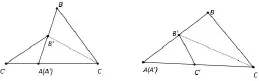
图4

注:共角比例定理的逆定理是证明两角相等或互补的一个十分有用的工具.

从共边三角形、共角三角形的定义我们可以看出,这两个模型在平面几何图形中普遍存在,那么共边比例定理与共角比例定理便可以大放异彩.以这两条定理作为基本定理,再辅以其他简单的几何命题,例如三角形内角和定理,圆的定义等就可以得到平面几何的一系列定理.在现行初中数学教科书中,某些定理的证明过程不够简洁或严谨,将共边比例定理、共角比例定理引入后,可以弥补这方面的不足.除此以外,这两个定理在解决较难或较复杂的几何题中,往往能发挥出意想不到的效果.从下面的例子体会这两个定理的美丽之处.

1 相似三角形的判定

在人民教育出版社义务教育课程标准试验教科书中数学九年级下学期(以下简称“《人教版数学教科书九(下)》”)中第二十七章第二节中介绍了相似三角形的判定.课本中先直接引入平行线分线段成比例定理,指导学生用度量线段的方法检验,并没有给出严格的证明.由平行线分线段成比例定理可以得到相似三角形的模型,然后推导出相似三角形的判定条件.这里,我们用“面积法”推导出相似三角形的判定条件.首先证明平行线分线段成比例定理.

平行线分线段成比例定理三条平行线截两条直线,所得的对应线段的比相等.上述定理可以写成:

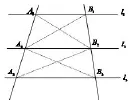
图5

如图5,直线l1、l2、l3互相平行,直线m、n分别交l1、l2、l3于

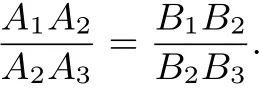
用“面积法”证明平行线分线段成比例定理比用度量法得到定理更能体现数学思维的严谨性,而且证明过程简单,证法直观、易懂.

三角形相似判定条件之一若△ABC与△A′B′C′中,∠A=∠A′,∠B=∠B′,则△ABC∽△A′B′C′.

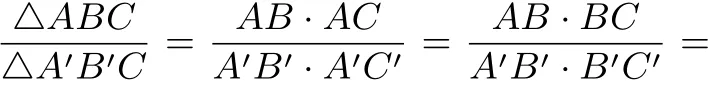
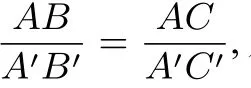
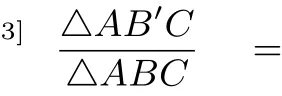
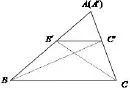
图6

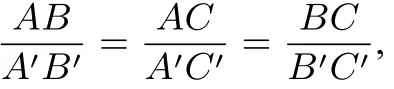
图7

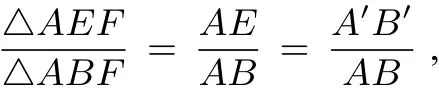
采用“面积法”的解题方法,应用共角比例定理来证明相似三角形的判定条件,相比起《人教版数学教科书九(下)》中对相似三角形的判定条件的证明更为简便、所用的知识储备更少.《人教版数学教科书九(下)》中需引入平行切割定理、全等三角形的知识来推导、证明,而这里只需用面积的简单推论和共角比例定理就可以得到,而且证明的过程简洁、易懂.

2 蝴蝶定理

设圆内的弦AB的中点为M,过点M作两弦CD、EF.连结CE、DF,分别交AB于G、H,则M为GH的中点.

分析:蝴蝶定理是初等几何著名难题之一,对蝴蝶定理的证明也有许多优美奇妙的解法,有添加辅助线的,也有解析几何的证法,但用面积法证明是最简单明了的,面积证法可以利用共边比例定理、共角比例定理或张角公式来得到面积与线段之比,不需添加辅助线.

证法一:如图8,由共边比例定理和共角比例定理得

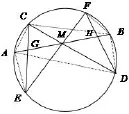
图8

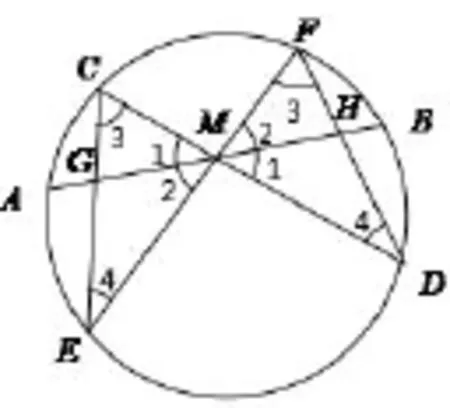
图9

证法三:此处给出欧几里得几何体系中的一种常用的证法.此证法需添加辅助线,用到全等三角形、相似三角形和四点共圆的知识点.

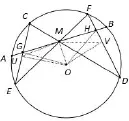
图10

如图10,连结OM,过圆心O作OU⊥CE,OV⊥FD,垂足为U、V,则OM⊥AB,U、V分别为CE、FD的中点.且由于∠GUO=∠GM=90°,∠HV O=∠HMO=90°得G、U、O、M四点共圆,H、M、O、V四点共圆.则∠CUM=∠GOM,∠MOH=∠MV F.又因为△CME∽△FMD,U,V为CE,FD的中点,所以,△CUM∽△FV M,∠CUM=∠MV F,所以,∠GOM=∠MOH,△GMO～=△HMO.所以,GM=HM.证毕.

通过对比以上三种不同的证明过程,我们体会哪种证法更优.在逻辑结构方面,逻辑结构越简单越好.从证明步骤看,证法三的证明步骤比证法一、证法二的证明步骤要多些,且需要添加辅助线得到全等三角形和相似三角形的模型才能解题,而这往往是我们解题时不容易想到的.从涉及的知识面看,证法三所涉及的知识点比较多,包括全等三角形的性质,相似三角形的判定,圆的性质定理,四点共圆的判定定理等.而用“面积法”证明不用添加辅助线便可得到共边三角形和共角三角形的模型,所用的定理主要是共边比例定理和共角比例定理,证明过程相对简便.

3 赛瓦定理

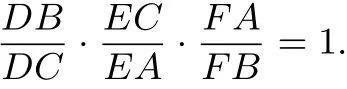
分析:要求线段之比,则可利用“面积法”的解题思想将线段之比变换成三角形面积之比,这里可以有很多不同的选择,只要使之满足三个比的积为1即可.[]3

用“面积法”证明赛瓦定理最能体现面积法解题的优越性,只需用共边比例定理或共角比例定理便可以得到,另外的证法可以用梅涅劳斯(Menelaus)定理来证明,同时梅涅劳斯定理也可以由面积法证得.

由以上几个简单的例子可以看出“面积法”的优点,特别是在解决数学奥林匹克的问题时,“面积法”的优势更为明显.将“面积法”的解题思想引入中学几何课堂,在中学课本中加入共边比例定理、共角比例定理这两个有力的解题法宝,能给学生提供多一种解题工具.同时,共边比例定理、共角比例定理的引入直观自然,知识的起点低,学生易于接受,并不会加重中学生的学习负担.以这两个定理作为基本定理,在课本中辅助推导证明其他的定理,能起到锦上添花的作用.学生在课堂学习中若能熟练运用“面积法”的解题思想来解决几何问题,那么学生解决几何难题的能力将会得到极大的提高.

[1]张景中,曹培生.从数学教育到教育数学[M].北京:中国儿童出版社,2005.2.

[2]张景中.一线串通的初等数学[M].北京:科学出版社,2009.12-13

[3]邱承雍.赛瓦定理及其应用[J].中学生数学,2012(02).

[4]张景中.教育数学探索[M].成都:四川大学出版社,1994.