动直角+定圆=轻松求线段最值

董浙南

在九年级的中考复习中，动点问题一直都是重点题型，而且常常以压轴题的位置出现，它蕴含着丰富的数学思想方法，需要学生具备良好的解题技巧和能力。而学生却因为找不到动点中的不动点，画不出运动轨迹，所以就找不到突破口。动直角是动点问题中的冰山一角，所谓“动直角”，是指角的顶点位置按照一定的规律轨迹在运动，并且角度始终是直角。所以，我们要解决利用动直角求线段的最值，首先要准确无误地画出该动直角顶点的运动轨迹（定圆），然后以不变应万变。但是要找到其中的不变，找到解决问题的突破口，对于学生来说，的确是件不容易的事。下面我仅从教学中遇到的几题提炼出其中一个类型，来阐述一种解题的教学方法。

例1 如图1，在平面直角坐标系中，将30°的三角尺的直角顶点O放在坐标原点，其斜边两端点A，B分别在x轴、y轴上，且AB=12cm。点C是平面内的一个动点，始终满足∠ACB=90°，求点C与点O之间距离的最大值。

学情分析：一般情况下，往往让我们求两点间距离的最小值，可以利用“两点之间线段最短”，也可以利用“垂线段最短”，但本题却求两点间距离的最大值。常规做法：用二次函数的形式来表示该两点间的距离，利用二次函数的最值来求解。可是，本题如若用函数思想来完成，学生几乎不知道该令什么是自变量，所以毫无头绪。

考点：圆周角定理；直角三角形斜边上的中线；两点之间线段最短。

分析：虽然点C是动点，但∠ACB=90°这个条件始终不变。利用“90°的圆周角所对的弦是直径”这一定理，从而找到一个以AB为直径的定圆，而点C的运动轨迹恰巧在该圆上。

解：如图2，∵∠ACB=∠AOB=90°

∴点C，O都在以AB为直径的圆D上

∴CO是圆D的一条弦

即当CO为直径时，CO最大

此时CO=AB=12cm

当然，利用三角形的“两边之和大于第三边”也可以解决。取AB中点D，连接CD与OD，因为CD=OD=6，所以当C、D、O三点共线时CO最大，等于12cm

总结：解决本题的关键在于能够找到点C在运动变化中的不变，并借助圆或三角形的有关知识点来解答问题，学生看到这样一个圆，问题就迎刃而解，充分体现数学中圆的四两拨千斤之功效。

例2 如图3，在边长为■的正方形ABCD中，动点F，E分别以相同的速度从D，C两点同时出发向C和B运动（任何一个点到达即停止），在运动过程中，求线段CP的最小值。

学情分析：一般情况下，求一条线段的最小值都是利用“垂线段最短”或是“两点之间线段最短”等知识点来解决的，但这道题利用以上两个常用的知识点无法解决，学生甚至都找不到不变的量，找不到CP最小时的位置，关键在于画不出点P的运动路径。

考点：圆周角定理；全等三角形的判定与性质；正方形的性质；点与圆的位置关系。

分析：首先对于即将参加中考的学生来说，看到图3，根据长期的解题经验，他们肯定可以得到△ABF≌△BCF，从而得到AE与BF垂直且相等，也就是说∠APB=90°恒成立。这样此题就比较明朗了，点P一定在以AB为直径的半圆上（如图4），当A、P、C三点共线时CP最小。

解：由题意得：BE=CF

∵AB=BC，∠ABE=∠BCE=90°

∴△ABE≌△BCF

∴∠BAE=∠CBF

∵∠CBF+∠ABF=90°

∴∠BAE+∠ABF=90°

∴AE⊥BF

∴∠APB=90°

即点P在以AB为直径的半圆O上，如图4

当点O、P、C三点共线时CP最短，等于OC-OP

此时CP=■-■

总结：本题的关键在于点P的运动轨迹，一旦朝这个方向想了，并且画出了准确的图，动中求静，使学生充分感受到解决动点问题的实质是变动为静、寻找不变的量。

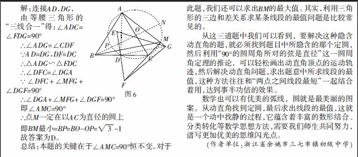
例3 （2015年武汉市中考第10题）如图5，△ABC，△EFG均是边长为2的等边三角形，点D是边BC，EF的中点，线段AG，FC相交于点M。当△EFG绕点D旋转时，线段BM的最小值是（）

A.2-■ B.■+1

C.■ D.■-1

考點：圆周角定理；相似三角形；等腰三角形。

分析：先考虑让△EFG和△BCA重合，然后把△EFG绕点D顺时针旋转，联结AG、DG，根据旋转角相等，旋转前后的对应线段相等，容易发现∠ADG=∠FDC，DA=DG，DF=DC，故∠DFC=∠DCF=∠DAG=∠DGA。又根据等腰三角形的“三线合一”可知∠FDG=90°，所以∠DFG+∠DGF=90°，即∠DFC+∠CFG+∠DGF=90°。所以∠AMC=∠MGF+∠CFG=∠AGD+∠DGF+∠CFG=∠DFC+∠DGF+∠CFG=90°。故点M始终在以AC为直径的圆上。

解：连接AD，DG，

由等腰三角形的“三线合一”得：∠ADC=∠FDG=90°

∴∠ADG=∠CDF

∵AD=DG，DF=DC

∴△ADG∽△FDC

∴∠DFC=∠DGA

∵∠DFC+∠MFG+∠DGF=90°

∴∠DGA+∠MFG+∠DGF=90°

即∠AMC=90°

∴点M一定在以AC为直径的圆上

即BM最小=BP=BO-OP=■-1

故答案为D。

总结：本题的关键在于∠AMC=90°恒不变。对于此题，我们还可以求出BM的最大值。其实，利用三角形的三边和差关系求某条线段的最值问题是比较常见的。

从这三道题中我们可以看到，要解决这种隐含动直角的题，就必须找到题目中所隐含的那个定圆，然后利用“90°的圆周角所对的弦是直径”这一圆周角定理的推论，可以轻松画出动直角顶点的运动轨迹，然后解决动直角问题，求出题意中所求线段的最值，这种方法往往和“两点之间线段最短”一起结合着用，达到事半功倍的效果。

数学也可以有优美的弧线，圆就是最美丽的图案。从动直角找到定圆，最后求出线段的最值，这就是一个动中找静的过程，它蕴含着丰富的数形结合、分类转化等数学思想方法，需要我们师生共同努力，谱写更加优美的思维闪光点。

（作者单位：浙江省余姚市三七市镇初级中学）