让学生经历学习数学的过程——小学数学探究性学习的五个特征

◎陈真真

让学生经历学习数学的过程
——小学数学探究性学习的五个特征

◎陈真真

探究的用法非常广泛，根据对探究和探究性学习过程的分析，探究性教学和学习在五个方面与科学探究有联系又有区别，这五个方面的特征构成了“让学生经历学习数学的过程”，即探究性学习的五个基本特征。

一、提出问题：学习者投入到对科学型问题的探索中

科学型问题，即符合客观规律的科学的问题，这些问题能引导学习者进行实证调查研究，通过动手操作或实验来收集和利用数据以形成对科学现象的解释。

在课堂里，提出对学生有意义的、有针对性的问题能够丰富学生的探究活动，但是它们不能是深不可测的，应该必须通过学生的观察和利用从可靠的渠道获得的科学知识能够来解决。学生必须掌握解答问题的基本知识和步骤，这些知识与步骤必须是便于检索和利用的，必须适合学生的发展水平。一开始提出的问题可以来自于学习者、教师、教材、网络和其它一些资源，有可能是结合起来产生。教师在引导和识别这些问题上起着关键的作用，熟练的教师能够帮助学生，使他们研究的问题更为集中、深入。例如学生们常常问“为什么”的问题，其中有些问题太大，教师可以把其中一些问题转变为“怎么样”的问题，这种改变使探究的问题更为集中、深入，更加接近科学，从而把学生导向科学探究，使学生能够体验到又有趣又丰富的调查研究结果。

例如在教学“东南西北”时，我先让孩子回忆学过的一篇文章——《方向》：“早晨起来，面向太阳，前现是东，后面是西，左边是北，右边是南，”学生问：“老师，为什么面向太阳，前面是东？”这时，我说：“因为太阳是从东边升起，那么我们在太阳底下会有一个影子，你会用影子辩认方向吗？除了用影子辩认方向，如果没有太阳，你还能用什么方法辩认方向呢？”从而把孩子引入怎样辩认方向的探究中。

在通过收集、探究之后，学生懂得了在野外时，苹果树上的苹果比较红的是南面，树叶比较稀少的是北面；在秋天的夜晚时，可以用北极星来辩认方向；在海上航船时，可以用指南针辩认方向。

二、收集数据：学习者重视实证在解释与评价科学型问题中的作用

在探究性学习中，学生也要根据实证资料作出对科学现象的解释。

（一）观察

例如，在教学《长方形的面积》一课时，我出示了4个大小、形状不同的长方形，并标上长和宽。

师：仔细观察这四个长方形，你觉得长方形的面积可能和什么有关呢？

（二）计算，记录

例如，在教学《长方形的面积》一课时，当孩子通过实验得出长方形的面积后，我引导学生：这个发现是否正确呢？这个方法是否对计算所有的长方形的面积都适用呢？接着，出示5个大小不同的长方形，让各小组任选一个长方形，组内学生一起验证——两个学生用刚才的方法测量，另两个学生用公式计算，看结果是否相同并做好记录。

（三）实验

将实验过程中的变化和发展情况记录在报告和表格中。例如，在教学《长方形的面积》时，我提出问题：“长方形的面积是不是与长和宽有关呢？下面我们做个实验，并填好表格。”（用面积为1平方厘米的小正方形进行粘贴）

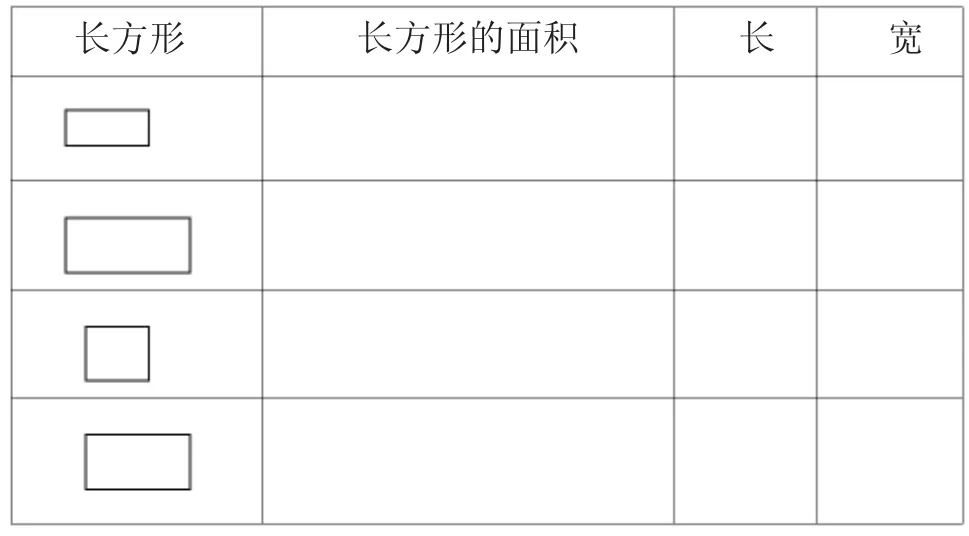
通过实验学生们知道：长方形面积所含的平方厘米数和长方形的长和宽有关，所以：长方形的面积=长×宽。

（四）探究

例如，在教学《圆的认识》一课时，我提出这样的一个问题：“回家去探究——车轮为什么是圆的？”从而让学生把所学的知识延伸到课外，并让学生经历通过各种各样的渠道收集信息和处理信息的能力，培养探究兴趣。

三、形成解释：学习者根据实证形成对科学问题的解释

所谓解释，指的是在学习新知识的过程中，将探究的结果与已有的知识联系起来，形成自己的结论。结论必须与实验或观察得来的实证材料相一致。学习者必须尊重事实，尊重规律，以开放的态度面对批评，运用与科学相联系的各种不同的认知过程——归类、分析、推论、预测，以及像批判性推理和逻辑等一般方法。

例如教学《三角形面积计算》中，在探究三角形面积计算公式时，我先让学生对三角形进行归类——直角、锐角、钝角，并让他们把三角形分类拼组成平行四边形或长方形。引导学生进行分析：三角形面积跟平行四边形有什么关系？由此来预测三角形面积的计算可能跟它自身的底和高有关。

四、评价结果：学习者根据其他解释对自己的解释进行评价

评价结果，即集体论证学习者个人的探究结果。学生们能通过参与对话比较各自的探究结果，或把他们的结果与教师或教材提出的结果相比较。

特别要注意的是：学生的科学性探究与科学家的科学探究不同，学生只要将他们的结果和适应他们的发展水平的科学知识相结合，就达到了探究性学习的目的。例如在教学《三角形面积的计算》一课时，学生经过动手操作实验之后明白三角形面积计算可能跟它自身的底和高有关，而后再把探究的结果与课本里的公式进行比较，从而达到探究的效果。

五、检验结果：学习者交流和验证他们提出的解释

科学家通过重复他人的实验来验证其结果。这就要求对问题、步骤、证据、提出的解释和对其他解释的评价进行明确清晰的描述。它使研究能够经受更多的质疑，也为其他科学家用这些解释来研究新问题提供机会。

让学生们交流他们的研究结果可以为其他人提供问题、检验实证材料、找出错误的推理、提出实证资料所不能证明的表述以及根据同一观察资料提出其它不同解释的机会。交流的结果能够引入新问题，或者加强在实证资料与已有的科学知识以及学生提出的解释之间已有的联系。结果是学生们能够解决交流中遇到的矛盾，进一步确定以实证为基础的论证方法。

“让学生经历学习数学的过程”，应充分体现这五个基本特征。当然这些特征都可以有所变化。例如，每一次探究都可以使学生投入到科学型问题中去，但是在有些情况下，探究的问题首先是由学生提出的，而有些情况下，学生并没有直接提出问题，而是在教师提供的问题中选择一个问题进行研究，或者在别人提出的问题上稍加修改，使之更为深入。研究表明，探究性学习中“让学生经历学习数学的过程”。学生的自主程度是很重要的，应该尽量使学生投入到自己发现问题或深化探究问题的活动中去。但是探究性学习也不是绝对的，只要围绕科学型问题的、使学生投入到思考中去的、适应特定的学习目标要求的，那么即使在这五个特征上有所变化，也可以认为是探究性学习。

（作者单位：福建省厦门实验小学）

（责任编辑：杨强）