应用型本科院校《微分方程数值解》课程教学改革的若干举措
——以黄淮学院为例
周红玲,沈 林
(黄淮学院 数学科学系,河南 驻马店 463000)
应用型本科院校《微分方程数值解》课程教学改革的若干举措
——以黄淮学院为例
周红玲,沈 林
(黄淮学院 数学科学系,河南 驻马店 463000)
针对黄淮学院微分方程数值解课程教学中存在的一些问题, 对该课程的教学进行了一些大胆的改革.主要介绍了课程在教学内容重组、模块化教学、实验教学、课程考核方式等方面的改革及其取得的成效.
微分方程数值解;应用型;教学改革
微分方程数值解是我校数学科学系信息与计算科学专业的专业必修课程,主要包括有限差分法、有限体积法、有限元法、变分原理和sobolev空间等内容的教学.同时由于其应用的广泛性也是一些院校理工科专业高年级学生的选修课程.
1 我校微分方程数值解课程教学中主要面临的问题
自升为本科院校后, 我校数学科学系信息与计算科学专业即开设了微分方程数值解课程.2014年前,该课程的教学主要存在以下几个问题:
第一,学时少内容难。我校信息计算科学专业的微分方程数值解课程的总授课学时为54学时,采用教材为李荣华老师、刘播老师编写的《微分方程数值解法(第四版)》,按照我校原教学大纲要求需讲授常微分方程初值问题的数值解法、椭圆型方程的有限差分法、抛物型方程的有限差分法、双曲型方程的有限差分法、边值问题的变分形式与Ritz-Galerkin法、Galerkin有限元法的教学内容, 而要完成以上内容的教学至少需要96学时,因此任课老师在讲授时只能把各章的部分重点讲到位,不可能做到面面俱到, 学生在学完一章后不能有一个整体的把握, 只记住了部分的重点,不利于学生后期的发展.同时,由于微分方程数值解中各种差分格式推导的烦琐性和各种格式相容性、稳定性、收敛性证明的复杂性,使得微分方程数值解课程被学生公认为本科阶段最难学的课程之一,大部分学生反映学完微分方程数值解课程后, 只记住了几个重要差分格式的收敛性等结论,而不知道具体怎么得来的,这有悖于我校现阶段“厚基础、重应用”中“厚基础”的原则.
第二,纯理论课程学习积极性减弱。我校原微分方程数值解教学大纲中设定54学时均为理论学时,由于课时紧张,任课教师在授课时往往采用“满堂灌”和“填鸭式”的教学方式,每一节课在简单复习上一节课的重点后,马上进入下一节的讲解,一章讲解完后,处理一下作业,紧接着进入下一章的讲授.学生在学完一章后,只记得一些零碎的差分格式及相关结论,不知道这些知识点除了解题外, 还有什么用途,就使得老师教的辛苦,学生学得迷茫.这有悖于我校现阶段“厚基础、重应用”中“重应用”的原则.
我校现阶段实行“3+1”的教学模式,而微分方程数值解课程开设于大三下半学期,也即是学生在校理论学习的最后一个学期.不考研的学生忙着选择实习单位,而考研的学生忙着复习专业课,对于纯理论课程的学习兴趣不高,达不到教学效果.
针对我校微分方程数值解课程教学中存在的一些问题,团队以坚持“特色鲜明的应用型本科高校”的办学定位为指导思想,对我校信息与计算科学专业的微分方程数值解课程教学进行了大胆改革.
2 我校微分方程数值解教学改革措施
2.1 重组教学内容实行模块化教学
由于我校信息与计算科学专业大三上学期开设的计算方法课程中已经详细讲解了常微分方程初边值问题的处理方法.因此,新的教学大纲中不在体现常微分方程初边值问题的数值解法.同时,在原有的54个学时中,团队拿出36个学时进行理论教学,那么再按教材讲解已无法完成教学任务.因此,团队对剩余教学内容进行了重组,并分5个教学单元进行教学.其中,教学单元1和5采用传统教学方式,教学单元1主要讲授微分方程数值解课程研究内容与考核方法;回顾常微分方程初边值问题的数值解法和偏微分方程等相关知识,为学生学好该课程打好基础.在教学单元5的教学中,团队弱化了教材中第5章边值问题的变分形式与Ritz-Galerkin法的讲解,重点让学生掌握变分原理和一些简单的sobolev空间, 为学生的深造打下基础.重组后,团队主要讲授3种方法:有限差分法(教学单元2)、有限体积法(教学单元3)、有限元法(教学单元4),其中重点讲授有限差分方法,具体课时分配及教学单元内容见表1.

表1 微分方程数值解教学单元及理论教学学时分配
为了适应现阶段应用型教学需求,有限差分法、有限体积法、有限元法采用模块化教学.例如有限差分法,主要从抛物型方程的有限差分法、椭圆型方程的有限差分法、双曲型方程的有限差分法等3个模块开展教学,每个模块的教学都设置了4个相同的教学过程:区域剖分、方程离散、初始和边界处理、性态研究,通过4个过程的学习,完成模块的学习(图1).对于各过程的教学,团队也作了详细的设置,区域剖分重点让学生学会矩形网的剖分和三角网的剖分;方程离散重点让学生掌握向前差分格式、向后差分格式、Crank-Nicolson差分格式;初始和边界处理主要讲授Dirichlet边界、Neumann边界、混合边界以及初始条件的处理.性态研究主要让学生了解各种差分格式稳定性、收敛性、收敛速度、误差分析(表2).由于3个模块的教学过程完全一致,因此只需将第1个模块的过程讲透彻, 剩下的2个项目的教学就比较容易了.
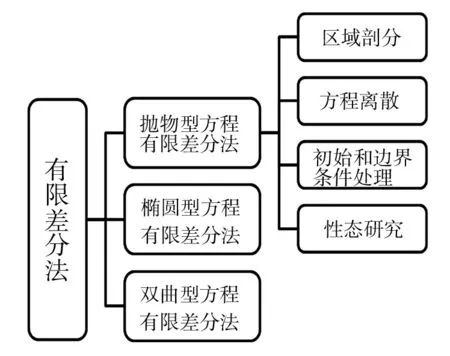
图1 有限差分法模块化教学安排结构
表2 模块化教学各过程知识点安排

教学过程知识点 区域剖分方程的离散初始和边界的处理性态研究1矩形网向前、向后差分格式Dirichlet边界稳定性2三角网Richardson差分格式Neumann边界收敛性3正六边形网Crank-Nicolson差分格式混合边界收敛速度4DuFort-Frankel差分格式初始条件误差分析
2.2 理论教学中融入实验教学环节
由于微分方程数值解课程理论性较强,为了使学生更好地掌握各教学过程,提高学生的数学应用能力,新教学大纲中,设置了18个学时的实验学时(实验学时安排见表3).实验教学分为热传导方程数值解法实验、Poisson方程数值解法实验、波动方程数值解法实验3个单元,每个实验单元6个学时.例如,在热传导方程数值解法实验中,设置的实验题目是:
求解一维热传导方程的初边值问题[1]141
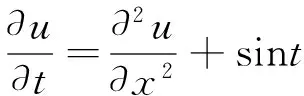
ux(0,t)=ux(1,t)=0,t>0,
u(x,0)=cosπx,0 表3 微分方程数值解实验学时分配 通过设置的实验可以检验学生对热传导方程有限差分法、有限体积法、有限元法的掌握.同时,也使得学生能够系统的运用所学知识解决问题,提高了学生学习的兴趣. 2.3 完善课程考核方式 课程的考核在教学环节中至关重要.课程考核不仅是检验学生掌握所学知识的程度,也是考查学生分析问题、解决问题能力的手段[2]5.我校微分方程数值解课程为考试课程,考核方式采用“6+2+2”方式.即“期终考试成绩+实验成绩+作业考勤成绩”,各自的比重60%、20%、20%. 期终考试是评估教学质量和学习水平的重要手段之一.根据课程的教学性质、教学目的、教学要求,重点考查学生对基本概念、常用差分格式和差分格式分析的掌握情况,特别对差分格式的应用性进行考核,以促进学生更好地掌握所学知识并强化学生的数学思维能力[3]29, [4]124-125.我校微分方程数值解课程期终考试的题型一般有选择题、填空题、计算题、证明题、综合分析题等五种题型,试卷整体综合性强且考察知识面广. 实验成绩主要取决于学生上交的实验报告,根据实验大纲中各个实验的要求,重点考查学生对所学知识的灵活运用能力,团队协作能力,论文撰写能力,程序编写能力等[5]96-97, [6]91-92.同时,任课老师通过作业的批阅和平时课堂考勤可以及时发现学生学习过程中出现的问题, 并予以纠正,达到敦促学生学习的目的. 近两年的教学改革和实践,得到了学生和院系的认可.学生们感觉采用这种教学模式不仅有利于学习微分方程数值解的各种差分格式,而且对实际问题处理的能力也有所提高, 激发了他们学习该课程的兴趣,同时拓展了他们的数学视野.院系老师也一致认为微分方程数值解课程在教学模式、教学内容、实验教学、考核方式等方面进行了大胆的改革与实践, 并取得了一定的成效.在后期的教学实践中团队将进一步完善模块化教学,利用学校资源实现教学手段现代化,努力使我校微分方程数值解的教学改革更彻底、更完善. [1] 李荣华, 刘 播.微分方程数值解法[M].4版.北京:高等教育出版社,2009. [2] 张宏伟.注重培养研究能力的《微分方程数值解法》课程教学研究与实践[J].大学数学,2006,22(06). [3] 廉海荣,赵琳琳, 陈瑞阁,等.关于“微分方程数值解”课研究型教学模式的探讨[J].大学数学,2012,28(05). [4] 杨 韧,杨光崇,谢海英.“微分方程数值解”的教学研究与实践[J].高等数学研究,2010,13(01). [5] 唐玲艳,屈田兴.微分方程数值解课程教学的实践与探索[J].湖南工业大学学报,2010,24(02). [6] 王保军,王景泉,徐国东.微分方程数值解教学实践的探究[J].南阳师范学院学报,2010,09(12). [责任编辑 梧桐雨] 2016-08-09 河南省教育厅教师教育课程改革研究项目“中学数学实验的开发设计与实施策略研究”(2016-JSJYYB-185) 周红玲(1981- ),女,河南西平人,黄淮学院数学系讲师,硕士,主要从事偏微分方程及其可视化研究。 G642;O241.8 A 1671-8127(2017)01-0085-04

3 结语

