一个不定积分的计算方法探讨

景慧丽，刘 华，赵伟舟

(火箭军工程大学 理学院， 陕西 西安 710025)

一个不定积分的计算方法探讨

景慧丽，刘 华，赵伟舟

(火箭军工程大学 理学院， 陕西 西安 710025)

针对一道不定积分的题目进行探讨，提出8种计算方法，即可以利用凑微分法、分部积分法、三角代换、根式代换等方法进行计算，有利于学员突破思维的局限性，进而培养学员的发散思维和综合能力.

不定积分；凑微分法；分部积分法；根式代换

0 引言

不定积分是微积分学中最基本的概念之一，能正确地计算不定积分是学员学习微积分必须掌握的基本能力之一.计算不定积分常用的方法有基本公式法、凑微分法(也叫第一类换元积分法)、第二类换元积分法和分部积分法[1]194-208等，当然每种方法都有自己的使用条件和适用范围.而且有的题目可以用多种方法来计算，有时计算结果形式上也会不一样，换句话说就是不定积分的计算比较开放，其实这种开放性对培养学员的发散思维很有帮助，因此，在教学中教员可以通过不定积分的计算来培养学员的发散思维.本文就一个不定积分题目的计算进行探讨，提出8种计算方法，进而培养学员的发散思维.

1 利用凑微分法

2 利用分部积分法

注2 分部积分法是计算两类函数乘积的不定积分的一种有效方法，遇到被积函数是两类函数的乘积的不定积分时，首先对其中一个函数(或构成这个函数的初等函数)求导，如果该导数等于另一个函数的常数倍，就可以用凑微分计算该不定积分；如果该导数不等于另一个函数的常数倍，就用分部积分来计算.

注4 分部积分可以多次使用，需要注意的是每次使用所选u的类型必须一致.

3 三角代换法

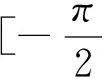
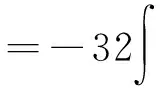
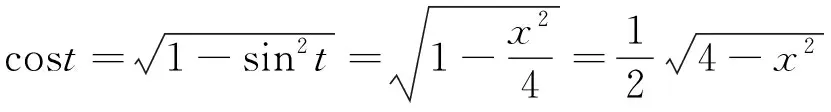
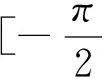
注7 在应用第二类换元积分法求解不定积分时一定要记着“回代”，即一定要把积分结果换成原来变量的函数[2]24-26.

4 根式代换法

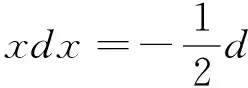
5 先恒等变形再利用根式代换

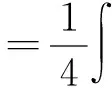
6 先恒等变形再利用整体代换

7 先利用换元积分法再利用分部积分法

8 结语

由上述计算方法可以看出，对一道题目的解法往往有不同的思路，知识点之间表面上看是相互独立的，实际上它们具有一定的联系.另外，高等数学课程中很多题目都可以用多种思路和方法来求解，教员在应用这类一题多解的题目组织教学时，必须以学员为本，鼓励学员积极参与教学活动，鼓励学员敢于标新立异，勇于提出问题、开展交流和讨论，这样才有利于学员突破思维的局限性，培养学员的发散思维和综合能力[3]24-26.

[1] 同济大学数学系.高等数学(上)[M].7版.北京：高等教育出版社,2007.

[2] 景慧丽.一道不定积分题的多种解法[J].玉溪师范学院学报，2016,32(04).

[3] 景慧丽，杨宝珍，刘 华，等.一个不等式的证明方法探讨[J].重庆工商大学学报(自然科学版)，2014,31(08).

[责任编辑 梧桐雨]

Research on Calculating Method for One Indefinite Integral

JING Huili, LIU Hua, ZHAO Weizhou

(SchoolofNaturalScience,theRocketForceUniversityofEngineering,Xi’an710025,China)

The papey discussed the subject for an indefinite integral and proposed eight kinds of calculation methods that can be used to scrape together differentiation, integration by parts, substitution triangle, radical substitution methods to help students break through the limitations of thinking and to cultivate students divergent thinking and comprehensive ability.

indefinite integral; improvising differential; integration by parts

2016-10-04

火箭军工程大学2015年度教育教学立项课题“基于高等数学课程教学的军校学员问题意识培养研究”(EPGC2015008)

景慧丽(1983- )，女，河南平顶山人，火箭军工程大学理学院副教授，硕士，主要从事最优化和大学数学教育研究。

O172.2

A

1671-8127(2017)01-0082-03