让错误成为一种课程资源

王伟云

摘要：在真实的数学课堂中，每天都有学生在出错，而错误中却蕴含着宝贵的课程资源。因此，我们要善待错误，让错误激发学生的学习兴趣；要捕捉错误，让错误点燃学生的创造火花；要珍视错误，让课堂在真实中演绎精彩；要诱发错误，在陷阱中培养学生的反思能力。课堂会因“错误”更加美丽。

关键词：错误；课程资源；学习兴趣；创造火花

中图分类号：G633.6 文献标识码：A 文章编号：1992-7711（2017）02-0067

错误是伴随学生学习过程出现的一种产物。只要有学习，就会有错误，它的出现是一种合理的现象。因此，我们教师，面对学生作业或练习中出现的错误，不必惊慌。它恰恰能反映学生在解题过程中的思维流露，也表现教师在教学过程的疏忽与缺漏。正视错误，利用错误，挖掘错误，把错误当作一种教学资源，不仅能够变废为宝，同时还能使数学课堂变得更加精彩。在实践中，笔者经常把错误当作资源加以利用，收到比较好的教学效果。

一、善待错误，激发学生的学习兴趣

“成功的教学所需要的不是强制，而是激发兴趣”。数学学习是不断假设、不断纠正错误的过程。面对错误，教师就要研究学生真实思维、反思自己的教学方法，进而激发学生的学习兴趣。而不应该批评指责，大声喝斥。

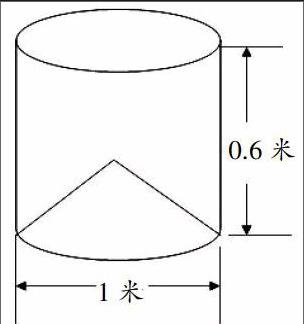
例如，学生在解下面这题时：（右图是一个酒厂蒸馏白酒用的集酒器，外形呈圆柱形，底面是一个向内凹进去的圆锥，高是圆柱的1/2，上面需加满冷水，求需加冷水部分的体积？）

大部分学生都用圆柱的体积减去圆锥的体积写出了这样的算式：3.14×0.52×0.6-1/3×3.14×0.52×0.3，可却有一位平时成绩优异的学生列出了这样的算式：3.14×0.52×0.6×5/3，很多学生因为看不懂算式，都在看着笔者，等待笔者的讲解。笔者没有直接指出学生的错误，而是让这位学生说说算理，该生在说的过程中发现自己的错误，并小声地说道：“不对啊，这样不是比圆柱体的体积还要大了吗？”然而，刚刚那几位迷惑不解的学生听了这位学生的讲解后却认为他说的有道理，很兴奋地叫道：“对的，对的。”刚刚那位学生又站起来说：“不对，这样算不是比圆柱体的体积还要大吗？”这时大家都觉得很好奇，疑惑到底错在哪里？进一步激起了他们的求知欲望。过了一分多钟，又是刚刚那位学生很兴奋地站了起来：“老师，我知道错哪里了，指着算式3.14×0.52×0.6×5/3，这里不是乘5/3而是乘5/6，因为需加冷水部分是这个圆柱体体积的5/6而不是这个圆柱体体积的5/3，是我把单位“1”弄错了。”在这位同学的启发和影响下，学生更加好奇，学习激情高涨，都不满足于此，于是他们又列出了3.14×0.52×0.3×5/3、1/3×3.14×0.52×0.3×5等算式。正是那位同学的错误激起了学生探究的欲望和学习兴趣，从而想出了更多的解题方法，也让课堂演绎了精彩。

二、捕捉错误，点燃学生创造的火花

课堂是动态发展的过程，错误随时可能发生。有些错误不可预见，有些错误防不胜防。教师只有独具慧眼，及时捕捉稍纵即逝的错误。把它当作教学资源，师生通过检查错误，反思错误，挖掘产生错误的内在因素，就可以点燃学生创造的火花，也能促进自己的教学机智。

例如，在教学习题时：小明每分钟步行18米，小东骑自行车20分钟行了1800米，小东每分钟骑的路程是小明每分钟行的路程多少倍？

方法一：1800÷20=90（米） 90÷18=5

方法二：18×20=360（米） 1800÷20=90（米）360÷90=4

当时，笔者没有马上说谁对谁错，只是让方法二的学生谈解题思路，他说：“小明20分钟行360米，小东每分钟骑90米，小明是小东的4倍。”当他说出的时候，马上发现了自己的错误之处，及时进行了纠正。列出了正确的算式：18×20=360（米）1800÷360=5。而且说出了想法。这时，大家都恍然大悟。可见，教师应有及时捕捉错误、让课堂在错误中“生成”的意识和能力，并让学生在探索中体验，在交流中辨明，在师生互动中共同创造、发展。

三、预设错误，让教学事半功倍

在教学实践中，我们常常会遇到一些容易出错的题目，教师可以利用这些易错点，凭借自己的经验，对容易错的种类、原因做出预判断，故意把容易发生错误的地方进行预设，诱导学生犯错，学生往往受到定势思维的影响，对事情缺乏细致、准确的理解，容易掉进教师所设的陷阱，然后在纠错过程中，明白错误的原因，真正了解题目的特征，提高解题思维。进而提高自主探究的能力。

例如，在教完《简便运算》这个单元后，笔者设计了这样一道有陷阱的题目：27+73×12，很多孩子受到前面凑整思想的影响，一心想着凑整，于是纷纷给出答案100×2=1200，这时有几个细心的同学叫道：“错了，不是先算加的，先加虽然方便，但是还是要遵循计算顺序的。”这时那些先加的同学纷纷叫道：老师坑人。师：如果要可以先算+再算×，题目应该要怎样修改？教师的问题引起了学生的思考，部分成绩优秀的孩子想到了答案：需要27也×12，这样才是27个12+73个12是100个12，才可以先加再乘。这时，教师不忘总结：可见要想先加再乘必须符合什么条件？“必须同时乘一个数。”经过此次“坑人”事件后，孩子们对此类题目的特点有了进一步的认识，再遇此类题目的时候明显注意了，在后面的作业中虽然还有个别孩子出现这种错误，但是只要一提醒你被“坑”了，孩子马上就知道了自己的錯因了，几次之后自然就记住了。乘法分配律的逆运算对孩子们来说是难点，经过这次的设“错”纠“错”之后，孩子们对乘法分配律有了更深的认识，学生学会了判断什么样的题目可以用乘法分配律，就会站在原认知的高度审视题目的特点，从而提高学习效果和效率。

总之，在教学过程中，把错误当作一作课程资源，有效地挖掘错误的价值，善待错误，及时捕捉错误，有效预设错误。这样，学生才能不断地从错误中走出来。数学课堂也会因此而变得更加精彩。