通过数学思维框架助推学生有效探究

徐丽峰+唐恒钧

【摘要】“探究教学”是我们高三课堂的重要课堂形式.通过数学思维框架建构，培养学生提出问题，解决问题的能力，推动探究课堂有效进行.同样，切实有效的“探究教学”促进学生学习与思考，完善学生的数学思维框架.

【关键词】探究教学；数学思维；起点性问题；通性通法

《普通高中数学课程标准（实验）》指出“倡导积极主动、勇于探索的学习方式”.单纯被动地吸收知识，并予以不断重复强化的学习，很难真正内化为学生自己头脑中的知识.只有让学生经历数学探究活动，知识才能真正得以内化，也才可能有所创造.目前中学数学的探究教学还存在比较多的问题.比如，由于起点性探究问题创设不恰当，导致学生探究目的不明确、探究低效；又如探究过程中教师引导过多，探究只有“形式”而缺乏实质；再如，在探究活动中学生只是完成教师给出的探究问题，而缺乏对问题提出过程的经历与思考.要让学生有效探究，并使其在不断深入的探究中发展数学能力，这需要教师创设恰当的探究脉络.这里的脉络既包括探究的起点问题，也包括使学生由起点问题引发新的探究问题的思维框架.本文将以笔者曾经实施的一次教学实践为例，探索通过数学思维框架助推学生有效探究的一些经验.

1案例简述

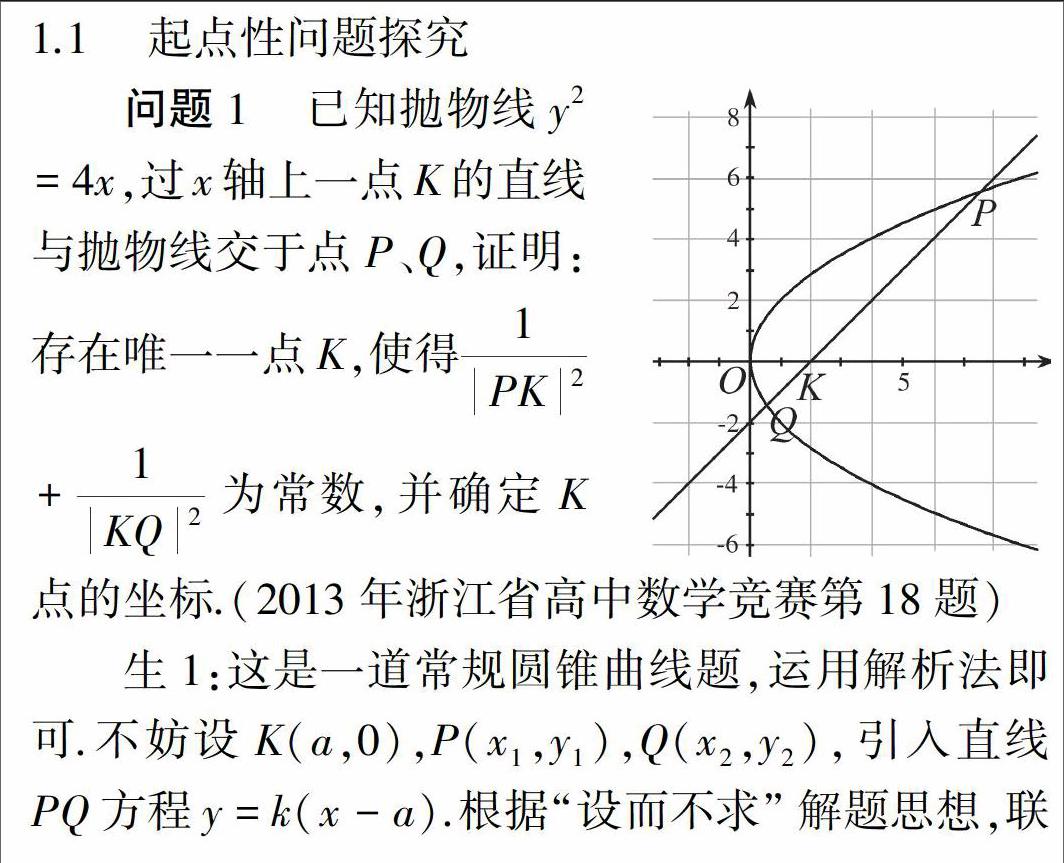
1.1起点性问题探究

1.2自然生成问题及其探究

1.3一般化问题的提出及解决

1.4课堂小结

师：经过一节课的探究学习，同学们有什么收获？

生11：这节课以“抛物线”为例，探究圆锥曲线中一类定点问题.解题方法常规，并没有涉及特别复杂计算.就椭圆部分比较麻烦，字母运算复杂，变量与参量容易搞混.但只要我们分清变与不变，大胆计算，成功离我们只有一步之遥.

生12：在问题探究过程中，体现很多数学思想方法，比如“逆向思维”、“一般化思维”、“特殊化思维”、“类比思维”.体现转化与划归、分类讨论、数形结合等数学思想方法，这是我们解决数学问题的通性通法.这些方法指引我们发现数学问题，解决数学问题，带领我们领略数学的奥秘……

师：这节课从抛物线展开，探究椭圆与双曲线.除了运用了解析法、“设而不求”等策略解题外，在从第一个关于特殊抛物线的定点问题到一般圆锥曲线的定点问题的讨论过程中，我们还可以看到问题变化过程中的逆向思维、一般化思维、特殊化思维、类比思维等一些基本思维方式.

2若干反思

2.1关注起点性探究问题的创设与提出

数学学习要养成善于思考、善于提出问题的习惯.李渺和单墫教授曾说过，不断地，持续地“思之、思之、思之、思之”，定有意想不到的收获[1]. “起点性探究问题”是探究型课堂的关键， 它应具备以下几个特点（1）起点性问题需要具有可变性、可拓展性，只有这样的问题才能形成有生命力的探究活动.（2）在实际教学中，起点性问题可以由老师提出，使后续探究活动具有一定指向性.中学课堂时间紧，课堂内容紧凑，这使得高中课堂探究活动不能完全自由，而需要有预设性的指向.比如本文中的竞赛题，问题指向一定范围，有助于触发学生有效思考与提问.生6围繞起点性问题的条件与结论互换，生7、生8将特殊问题推广至一般问题.教师平时要注意收集经典的好题和教学案例等素材，注意掌握引导学生开展探究性活动的经验.并通过起点性问题的设计，在教师引导与学生探究间取得平衡.

2.2关注以数学思维框架作为学生探究活动的先行组织者

数学是锻炼思维的体操，高质量数学学习以数学思维作为首要基础.练习数学解题是数学学习的较低层次，更重要的是在解题过程中形成具有一般意义的数学思维框架.通过对2013年浙江省数学竞赛第18题的探索，生6逆向思维和生7、生8特殊问题一般化思维、类比思维，推广得到任意抛物线、乃至一般圆锥曲线中有关定点的结论，这些都体现数学思维方法在数学解题以及提出问题中的价值.在这节课中，通过教师的引导与学生的实践，试图让学生形成用三种思维进行数学问题的探究：（1）学会一般性与特殊性转换思维，复杂即简单，简单即复杂.（2）学会逆向思维，从条件到结论，从结论到条件，理解问题的基本结构.（3）学会通过一般化思维、类比思维，使问题得到推广.教师要充分挖掘来源于学生提问、数学作业等探究性资源，以此为契机，建构循序渐进研究问题的数学思维框架，增强学生自我破体能力[2].

2.3关注在一类问题的探究过程中并形成通性通法

通性通法，是指具有某些规律性和普遍意义的常规解题模式和常用的数学思想方法.数学试题的形式和知识背景可能会千变万化，但其中运用的数学思想方法却往往是相同的.例如本题中，贯彻“设而不求”解题，将直线方程代入圆锥曲线方程，整理成一元二次方程，再利用根的判别式、求根公式、根与系数的关系等通性通法.在数学的学习和解题过程中思维起主导作用，老师在教学时要更多地注重“一题多变”；更多地注重引导学生体验问题提出及解决过程中所渗透的一般性的数学思维方法，以及一类问题的通性通法.

总之，探究性学习有助于学生数学能力的发展.本文试图通过一次教学实践案例，讨论如何让学生通过起点性问题的探究，在数学思维框架的引导下生成新的、更具挑战性问题，并在解决这类问题的过程中学习通性通法.当然，这方面的研究还需要更多的实践探索.

参考文献

[1]李渺，单墫.解题中的形象思维[J].数学通报，2006（5）：51-53.

[2]孙小龙.问题打破预设，师生生成探究[J].中学教研（数学），2016（8）：19-22.