一种基于最大Lyapunov指数奇异分解的并行挖掘算法

文政颖，李运娣

(河南工程学院 计算机学院,河南 郑州 451191)

一种基于最大Lyapunov指数奇异分解的并行挖掘算法

文政颖，李运娣

(河南工程学院 计算机学院,河南 郑州 451191)

针对当前大数据挖掘并行计算采用多元线性回归分析方法导致的计算开销过大、挖掘准确度不高等问题，提出了一种基于最大Lyapunov指数奇异分解的大数据挖掘并行计算方法.该方法对大数据信息流进行高维相空间重构和QR分解，计算大数据流模型的最大Lyapunove指数谱，基于微积分极值理论构建大数据的Lyapunove指数谱的网格分布矩阵，采用奇异值分解方法对参与运算的大数据特征向量矩阵行分解，将大规模的数据挖掘计算问题变为一系列小规模的并行计算问题，实现了大数据挖掘中并行算法的改进.测试结果表明，采用该方法进行大数据挖掘的计算时间较短、内存开销较小、准确度高.

大数据；挖掘；最大Lyapunove指数；奇异值分解；并行算法

数据挖掘是通过提取数据信息流中的有用特征来估计数据中的关键信息参量，以实现数据采集和参量估计.大数据挖掘中的并行算法是在分布式云计算环境下进行数据的并行调度和网格化多线程处理的[1]，为了提高大数据的挖掘效率，需要进行数据挖掘的并行算法优化，研究大数据挖掘并行算法在数据库构建、云计算信息处理等领域也具有较高的应用价值.

传统方法中对大数据挖掘的并行处理主要有基于数据特征量的LU分解方法、QR分解方法与基于数据并行调度的块匹配方法等[2-5].随着大数据信息处理技术研究的不断深入，对大数据挖掘的并行计算受到了相关学者的重视，取得了一定的研究成果.文献[6]采用海量散乱点云快速压缩方法进行海量云大数据的并行计算，对数据信息流进行互信息特征的提取，对提取的互信息特征采用支持向量机进行误差修正，以提高数据并行计算的能力，但该算法应用于矩阵秩亏损大数据挖掘中收敛性不好，对求解大规模数据挖掘问题不适用.文献[7]采用多元线性回归分析方法进行大数据并行计算,实现数据拟合、参数估计和系统辨识，该方法在进行高维数据计算中容易导致计算开销过大、挖掘准确度不高等问题[8].针对上述问题，课题组提出了一种基于最大Lyapunov指数奇异分解的大数据挖掘并行计算方法,计算大数据流模型的相空间重构轨迹和最大Lyapunove指数谱，构建大数据的Lyapunove指数谱的网格分布矩阵，采用奇异值分解方法对参与运算的大数据特征向量矩阵行分解，将大规模的数据挖掘计算问题变为一系列小规模的并行计算问题，最后进行仿真测试，得出了有效性结论.

1 大数据信息流高维相空间的重构和特征提取

1.1 大数据信息流高维相空间的重构

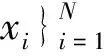
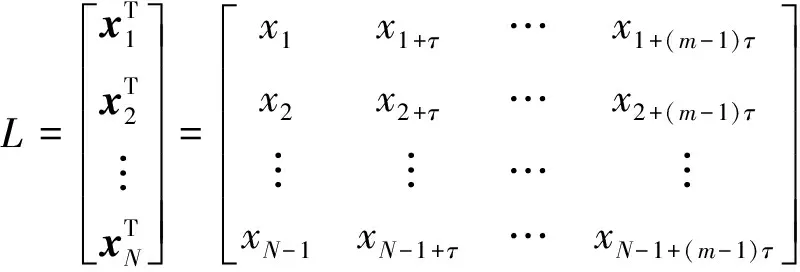
(1)

式中:m为海量大数据序列中的特征信息关联维数；τ为相空间中的嵌入时间延迟.在重构数据映射的m维相空间内，构建对大数据挖掘的稀疏矩阵L，进行奇异值分解L=U×S×C，U和C是高阶特征系矩阵，

C=(c1,c2,…,cn).

(2)

将映射u→uλ代入泛函性平衡解中，在有限域的线性子空间中存在广义逆正解，S为L的奇异值，且

S=diag(σ1,σ2,…,σn),σ1≥σ2≥…≥σn≥0.

(3)

对任意一个正交矩阵，在线性子空间中得到高维相空间中大数据信息流并行计算的轨迹的欧式距离满足

‖xj-xi‖≤ε，

(4)

式中：ε是足够小的正数，由此可确定xj，从而组成一个大数据并行挖掘特征挖掘的邻域矩阵：

Bxi=(δxi(j1),δxi(j2),…,δxi(jNb))T.

(5)

通过上述相空间的重构，在高维相空间中进行最大Lyapunove指数谱特征的提取，构建了高维特征矩阵，采用特征压缩方法将高维矩阵转换为低维矩阵，降低了运算的复杂度.

1.2 最大Lyapunove指数谱特征的提取

通过提取大数据信息流的最大Lyapunove指数谱，实现大数据挖掘的并行处理[9].计算在相空间内的数据序列映射向量{δxi+1(jk)=xjk+1-xi+1|k1,…,Nb}，重构数据映射的m维相空间，采集一维数据矢量Xn，又得一个邻域矩阵：

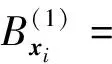
(6)

当ε足够小，当相空间嵌入维数m增加到m+1时，有

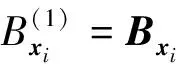
(7)

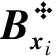
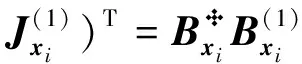
(8)

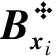
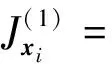
(9)

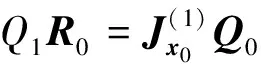
(10)

在大数据挖掘过程中，数据信息流的最大Lyapunove指数谱通过自适应泛函通向局部收敛，有

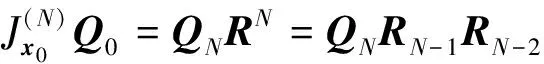
(11)

对全部Q0，大数据信息流的Lyapunove指数谱特征收敛于

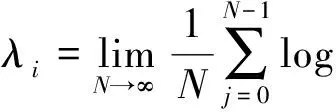
(12)

2 数据挖掘并行算法的改进

2.1 大数据挖掘并行处理中的矩阵分解

在进行了上述最大Lyapunove指数谱特征提取的基础上，进行大数据挖掘并行计算，提出了一种基于最大Lyapunov指数奇异分解的大数据挖掘并行计算方法，待挖掘的大数据信息流为

(xi1,xi2,…,xi,m-1,yi),i=1,2,…,n.

(13)

对大数据挖掘的并行计算问题就是求向量β的一致性估计的最小二乘问题，为了使‖Y-Xβ‖达到最小，对于有因变量自变量的n组观测大数据(xi1,xi2,…,xi,m-1,yi)求解

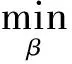
(14)

采用奇异值分解方法对参与运算的大数据特征向量矩阵行分解，进行大数据挖掘的并行计算.

2.2 大数据挖掘并行计算的优化

采用最大Lyapunove指数谱特征矩阵的奇异值分解方法，设A∈Rn×m且秩为r的非零矩阵，n和m都是正整数，考虑第i次迭代，输入为双端块雅克比向量Y(i)和奇异矩阵X(i)，矩阵维数分别为N(i)×1和N(i)×m.在大数据信息流的特征分解过程中，矩阵X(i)被分解为p(i)个大小为Nij×m的子矩阵Xij，将矩阵X进行奇异值分解，X=UΣVT，求大数据信息流Lyapunove指数谱的子矩阵最小二乘解.这里,Nij≥m，对于大数据挖掘的重构特征矩阵A，存在n阶正交矩阵U和m阶正交矩阵V，对第j个奇异值分解矩阵Xij进行非零特征值分解：

Xij=UijΣijVijT.

(15)

β*=V(k)1Σ(k)1-1U(k)1TY(k)，

(16)

式中：V(k)，Σ(k)1，U(k)1为X(k)进行奇异值矩阵分解运算所得.限于篇幅，并行算法伪代码省略.

采用奇异值分解方法进行数据挖掘的特征分解和并行处理，对参与运算的大数据特征向量矩阵行分解，子矩阵之间是完全独立的.对p(i)个子矩阵，奇异值分解运行能在数据挖掘过程中并行处理，从而加快了运算速度，降低了大数据挖掘并行运算的开销，提高了计算效率.

3 实验与分析

为了测试本算法在实现大数据挖掘并行运算中的性能，进行数据挖掘并行运算对比仿真实验，实验平台采用的CPU是四核八线程的，软件采用Matlab7仿真平台，使用大型网络数据库OpenMP2.0和MPICHNT1.2.5中的数据为测试样本数据集，分别取其中的6组数据样本进行大数据挖掘并行运算仿真分析，图1给出了其中一组数据的时域波形.

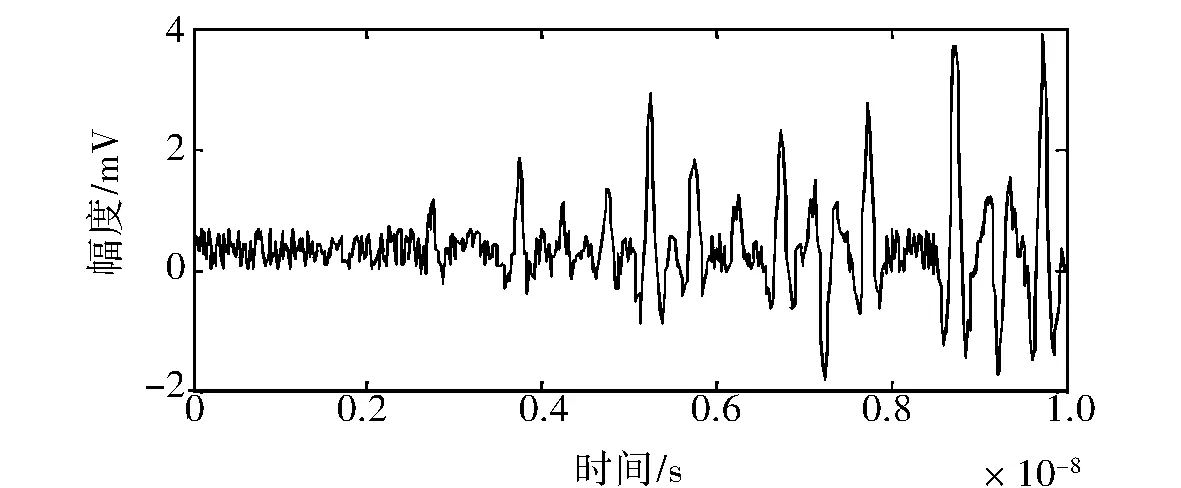
图1 大数据信息流时域波形Fig.1 Time domain waveform of large data information flow

对图1所示的大数据信息流进行特征提取和挖掘分析，计算大数据流模型的最大Lyapunove指数谱，得到Lyapunove指数谱，如图2所示.图2中，4条谱线中收敛值最大的谱即最大Lyapunove指数谱.

以计算得到的Lyapunove指数为特征参量，构建大数据的Lyapunove指数谱的网格分布矩阵，采用奇异值分解进行并行运算，实现大数据挖掘.为了对比性能，采用并行算法和传统的串行算法进行数据挖掘的时间开销对比，结果如图3所示.

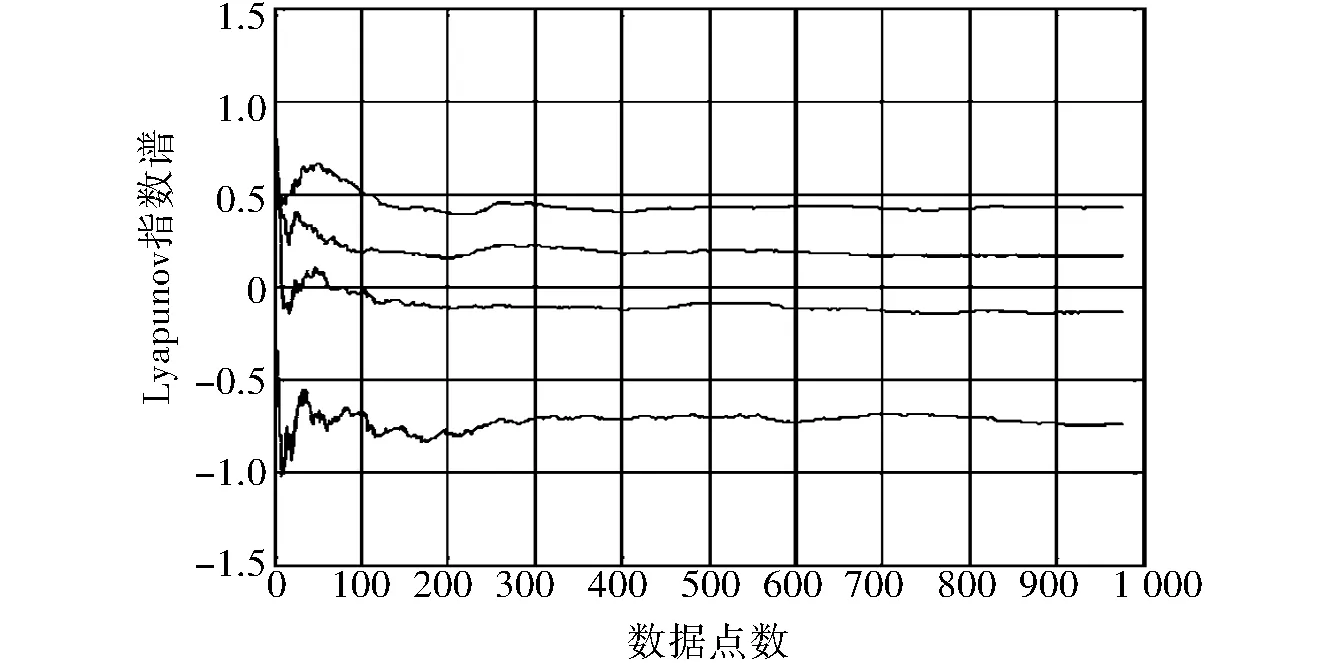
图2 大数据信息流的Lyapunove谱特征提取Fig.2 Lyapunove spectrum feature extraction of large data stream

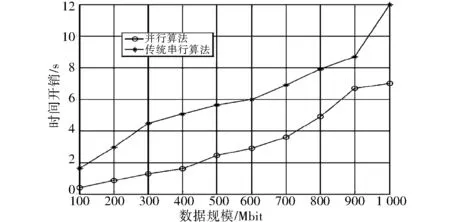
图3 运算时间开销对比Fig.3 Operation time overhead contrast

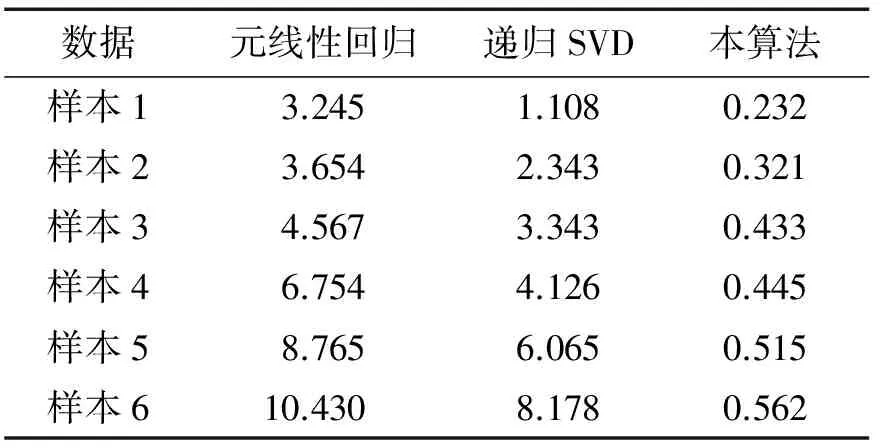
Tab.1 Memory consumption M

分析图3可知，采用并行算法进行大数据挖掘的时间开销较小.表1给出了不同算法进行数据挖掘的内存开销.分析表1可知，随着数据规模的增加，内存开销加大，传统方法内存开销的增长幅度较大，严重占用了计算的内存，而本算法的内存开销远小于传统方法，受大数据运算规模的影响较小，特别适合用于海量数据的挖掘.因此，采用本算法进行并行运算，降低了内存开销，提高了运算性能.

4 结语

为了提高大数据挖掘的效率和准确性，本研究提出了一种基于最大Lyapunov指数奇异分解的大数据挖掘并行计算方法.该方法对大数据信息流进行高维相空间的重构和QR分解，计算大数据流模型的最大Lyapunove指数谱，基于微积分极值理论构建了大数据Lyapunove指数谱的网格分布矩阵，采用奇异值分解方法对参与运算的大数据特征向量矩阵行分解，将大规模的数据挖掘问题变为一系列小规模的并行计算问题，实现了大数据挖掘中并行算法的改进.实验证明，采用本算法进行大数据挖掘并行运算处理的计算开销和内存开销都较小，运算效率得到了提高.

[1] 邢淑凝,刘方爱,赵晓晖.基于聚类划分的高效用模式并行挖掘算法[J].计算机应用,2016,36(8):2202-2206.

[2] ZIHAYAT M,AN A.Mining top-k high utility patterns over data streams[J].Information Sciences,2014(285):138-161.

[3] YUN U,RYANG H,RYU K H.High utility itemset mining with techniques for reducing overestimated utilities and pruning candidates[J].Expert Systems with Applications,2014,41(8):3861-3878.

[4] SONG W,LIU Y,LI J.Mining high utility itemsets by dynamically pruning the tree structure[J].Applied Intelligence,2014,40(1):29-43.

[5] HIE B E,HSIAO H F,TSENG V S.Efficient algorithms for discovering high utility user behavior patterns in mobile commerce environments[J].Knowledge and Information Systems,2013,37(2):363-387.

[6] 方芳,程效军.海量散乱点云快速压缩算法[J].武汉大学学报(信息科学版),2013,38(11):1353-1357.

[7] LEE D,PARK S H,MOON S.Utility-based association rule mining:a marketing solution for cross-selling[J].Expert Systems with Applications,2013,40(7):2715-2725.

[8] 闫昭,刘磊.基于数据依赖关系的程序自动并行化方法[J].吉林大学学报(理学版),2010,48(1):94-98.

[9] 杨景明,侯宇浩,孙浩,等.采用数量级阈值与二维信息排序策略的NSGA-II-DE算法[J].控制与决策,2016,31(9):1577-1584.

[10]张景祥,王士同,邓赵红,等.融合异构特征的子空间迁移学习算法[J].自动化学报,2014,40(2):236-246.

A parallel mining algorithm based on maximal Lyapunov exponent singular decomposition

WEN Zhengying，LI Yundi

(CollegeofComputer，HenanUniversityofEngineering，Zhengzhou451191，China)

In view of the current data mining parallel computing method of regression analysis leads to excessive computational overhead by using multivariate linear, mining accuracy is not high, in order to improve the efficiency and accuracy of data mining, a large number of maximum Lyapunov Exponent Based on singular decomposition according to the parallel computing method of mining. For phase space reconstruction and QR decomposition of large data flow, the maximum Lyapunov index calculation of large data flow model of the spectrum, constructing the grid distribution matrix data Lyapunov exponent spectrum calculus based on extreme value theory, using singular value decomposition method for participating in the operation of large numbers according to the eigenvector matrix decomposition, large-scale data mining the calculation problem into a series of small scale parallel computing problem, improved algorithm in data mining. Experimental results show that the proposed method is used for large data mining, the computation time is relatively short, the memory cost is small, and the accuracy of data mining has been greatly improved.

big data; mining; maximum Lyapunov exponent; singular value decomposition; parallel algorithm

2016-10-12

河南省高等学校重点科研项目(16A520004)

文政颖(1979-)，女，河南南召人，副教授，主要研究方向为图像处理与计算机应用.

TP312

A

1674-330X(2017)01-0067-04