物联网节点需求量计算方法
何 莉,李 博
(河南工程学院 计算机学院,河南 郑州 451191)
物联网节点需求量计算方法
何 莉,李 博
(河南工程学院 计算机学院,河南 郑州 451191)
物联网节点覆盖的全面性和连通性直接关系着对物理空间监控的有效性.当前,人们对二维空间覆盖问题研究得较多,但随着物联网应用领域向空中和水下延伸,三维空间节点覆盖问题亟待解决.现有的三维空间k-覆盖问题的解决方法通常是1-覆盖问题解决方案的简单扩展,存在一定的局限.在总结现有研究结果的基础上,提出了一种新的三维空间k-覆盖节点数量快速计算方法,利用指数增长方法快速确定节点需求量的充分值,然后利用分治策略快速定位节点需求量的必要值,实验结果证明新方法具有较强的适应性且更加贴合实际.
k-覆盖; 分治策略;三维空间覆盖问题
物联网被誉为继计算机和Internet之后世界信息产业发展的第三次浪潮.物联网从物理世界获取信号,经信息系统处理后,反作用于物理系统.物联网信息系统工作的有效性取决于物理信息获取的全面性.因此,要有效监控物理空间,就要先解决物联网节点的覆盖问题,这是物联网研究与应用的基础.
物联网二维空间覆盖问题的研究成果[1]较多.随着物联网在空中和水域的应用,三维空间的覆盖问题逐渐成为研究热点.三维空间覆盖问题的复杂度远高于二维空间,不能简单地从二维空间的研究成果推广应用于三维空间.三维空间的覆盖问题分为1-覆盖和k-覆盖问题,1-覆盖问题可以看作k-覆盖问题的特例,即k=1时的情况.现有研究分别从子空间划分和节点部署最低密度的角度尝试解决1-覆盖问题,并从空间角度将1-覆盖问题的研究成果推广到k-覆盖问题[2].子空间划分的基本思想是在节点的通信距离与探测距离比率确定的情况下,选取合适的三维立体空间结构为基本单元,无缝填充覆盖目标,节点部署在每个基本单元的几何中心.对于1-覆盖,通常在每个单元放置1个节点;对于k-覆盖,每个单元放置k个节点.为满足活动节点需求量最少且保证节点连通性的条件,感知距离至少是通信距离的0.542 326倍.当节点的通信距离和探测距离的比率不同时,选取不同的多面体满足1-覆盖三维空间[3].节点最低密度求解方法的基本思想是对于给定空间中的任何一个点,要满足1-覆盖或k-覆盖条件,确定在空间中需要部署的节点的最低密度[4].
现有研究存在的待改进之处:①对于子空间划分方法,k-覆盖问题的解决方法是在1-覆盖基本单元几何中心放置k个节点,在理论上是可行的,但考虑到节点本身需要占据一定的空间及从安全角度来说,多个节点并不适合于集中放置,所以在实际部署时这种方法存在不合理之处;②现有方法侧重于覆盖率,通常假设节点探测距离与通信距离满足一定的约束条件时节点的连通性得到满足,当约束条件改变时,需要复杂的计算才能获得节点的需求量.
基于以上不足,课题组提出了一种新颖的节点需求量计算方法以解决物联网空间k-覆盖问题.给定节点探测距离r,新方法能够计算通信距离d和k取不同值时节点的需求量.
1 相关假设与定义
首先,对物联网进行必要的假设和定义.
为了便于研究三维空间的覆盖问题,将连续空间覆盖问题转化为离散空间覆盖问题.具体步骤为在三维空间S的3个方向X,Y,Z分别进行等间隔划分,等分线交叉形成的点构成集合Ω,点的数量用‖Ω‖表示,每个点i的空间坐标用Loc(i)=(xBi,yBi,zBi)表示,下标B表示这些离散点为基准点(benchmark points),1≤i≤‖Ω‖.
对物联网的假设如下:物联网节点部署后位置不变,节点之间一旦建立连接,该连接在节点存活期内不会中断;物联网的节点是同质的,即具备相同的通信距离、感知距离和初始能量;节点s的感知距离为r,感知范围是以节点所在位置(xs,ys,zs)为中心的球体;设节点的通信距离为d,当两节点之间的欧氏距离不大于d时,两节点可以建立通信.
对物联网的定义如下:在三维空间S中部署m个节点,节点构成集合V,节点之间的相互连接(称为无向边)构成集合E,节点和边构成图G=(V,E).
定义1 连通性.如果图G=(V,E)中任何两节点之间都存在一条路径,那么物联网是连通的.节点连通率φ(m)定义为监控空间部署m个节点后图G的最大连通图的节点数与图G的全部节点数的比率.设G′=(V′,E′)表示图G的最大连通子图,那么
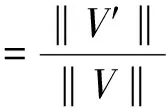
(1)
节点连通率坡度φ′(m,n)定义为
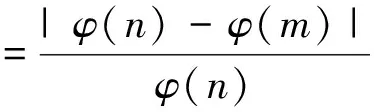
(2)
式中:φ(m)和φ(n)分别表示监控空间部署m和n个节点的节点连通性;φ′(m,n)表示部署不同数量的节点连通性的相对变化,将作为迭代寻找节点需求量的终止依据.
定义2k-覆盖的定义.如果空间中某点i位于至少k个节点的感知范围内,那么该点i是k-覆盖的.当k=1时,点i是1-覆盖的.如果三维空间S中任何一点都是k-覆盖的,那么空间S是k-覆盖的.
三维空间中部署的节点i的坐标为(xi,yi,zi),1≤i≤m.每个节点i能够监测的离散点集合用SR(i,r)表示,集合Ω中满足k-覆盖的点集用Ωk表示.
k-覆盖率ηk(m)定义为监控空间部署m个节点后集合Ω中满足k-覆盖的节点占的比例,表示为
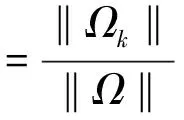
(3)
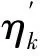
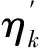
(4)
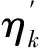
定义3k-覆盖问题.在三维空间中至少需要多少个节点以满足监控目标空间是k-覆盖的条件,并且要保证这些节点是连通的.k覆盖问题用数学描述如下:
maxy=f(X)=[ηk(m),φ(m)],
(5)
式中:ηk≤1;φ≤1;X={(x1,y1,z1), (x2,y2,z2), …, (xm,ym,zm)},表示所部署节点的坐标的集合,m∈Z+.
2 k-覆盖节点数量的计算方法
三维空间的k-覆盖问题最优化已被证明是NP优化问题,本课题提出了一种近似最优化方法来解决这个问题.
2.1 基本方法
在给定的三维空间S中,当部署的节点数量较少时,只有部分节点能连通且只有部分空间是k-覆盖的.随着部署节点数量的增加,节点的连通率和监控空间的k-覆盖率都会得到改善.节点的连通率和空间的覆盖率是影响节点需求量的主要因素,为区分这两个因素对节点选择的影响,节点数量的计算分3个阶段进行.
(1)仅根据节点连通率计算节点需求量
节点连通率主要与节点的通信距离有关,与节点的覆盖距离没有关系.可以预见,为达到一定的节点连通率,随着节点通信距离的增加,节点数的需求量将减少,这个阶段获得的节点数量记为mconn.
计算mconn的问题可分解为两个子问题:①充分性问题,即尽快找到一个节点数量,能够满足节点连通率φ(m)等于1或接近1;②必要性问题,即最低需要部署多少个节点才能够满足条件.
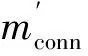
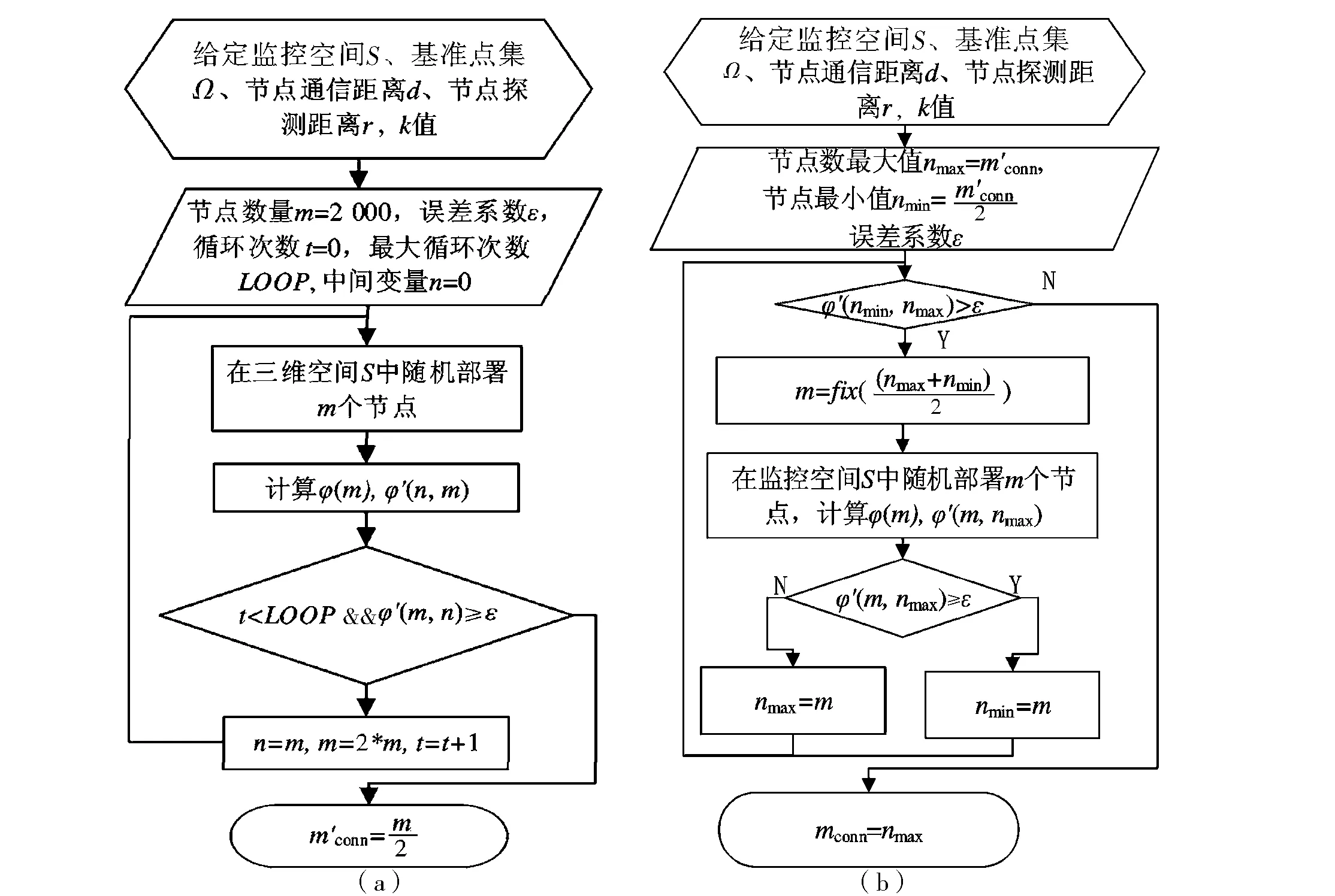
图1 节点需求量的计算流程Fig.1 Flow chart for computing node demand
(2)仅根据空间覆盖率计算节点需求量
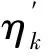
(3)综合考虑节点连通率和空间覆盖率来计算节点需求量
令mcomplete=max(mconn,mcover).当监控空间S部署mcomplete个节点后,可以同时实现节点连通率和空间k-覆盖率等于100%或接近100%.
2.2 方法分析
将节点需求量的计算过程分为3个阶段,主要考虑不同因素对计算的影响,也便于有针对性地分析影响因素.
在第1阶段第(1)步,找到满足条件的节点数,节点数的增长方法有多种选择,如线性增加、指数增加等.若采用线性增加方法,需要事先确定每次增加的节点数,即步长.如果步长选取过小,需要多次迭代才能满足要求;若步长过大,虽然迭代次数减少,但依然存在冗余.因此,步长的合理选择存在一定的困难.采用指数增加的方法,即使初始节点选取较小,由于每次迭代节点数量成倍增加,也可以迅速找到满足条件的节点数.因此,指数增加的方式相对于线性增加具有一定的优势.
在第1阶段第(2)步,在[nmin,nmax]中搜索节点必要值,可以选择线性搜索、分治策略等.和线性搜索相比,分治策略搜索的计算量比较小.
通过引入最大循环变量LOOP和误差系数ε,在满足一定精确度的同时,提升了程序的稳定性.
第1阶段的算法复杂度主要由计算节点连通率决定,而计算节点连通率的复杂度主要由计算最大连通子图决定.第2阶段的算法复杂度主要由计算空间k-覆盖率决定,其算法复杂度为Θ(n2).
3 实验
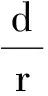
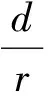
新算法能够计算出不同k-覆盖对应的节点需求量.k取值由1增加到5,步长为1,不同k值对应的节点需求量如图3所示.从图3可以看出,随着k值的增加,节点需求量也逐渐增加,但增长率低于k.
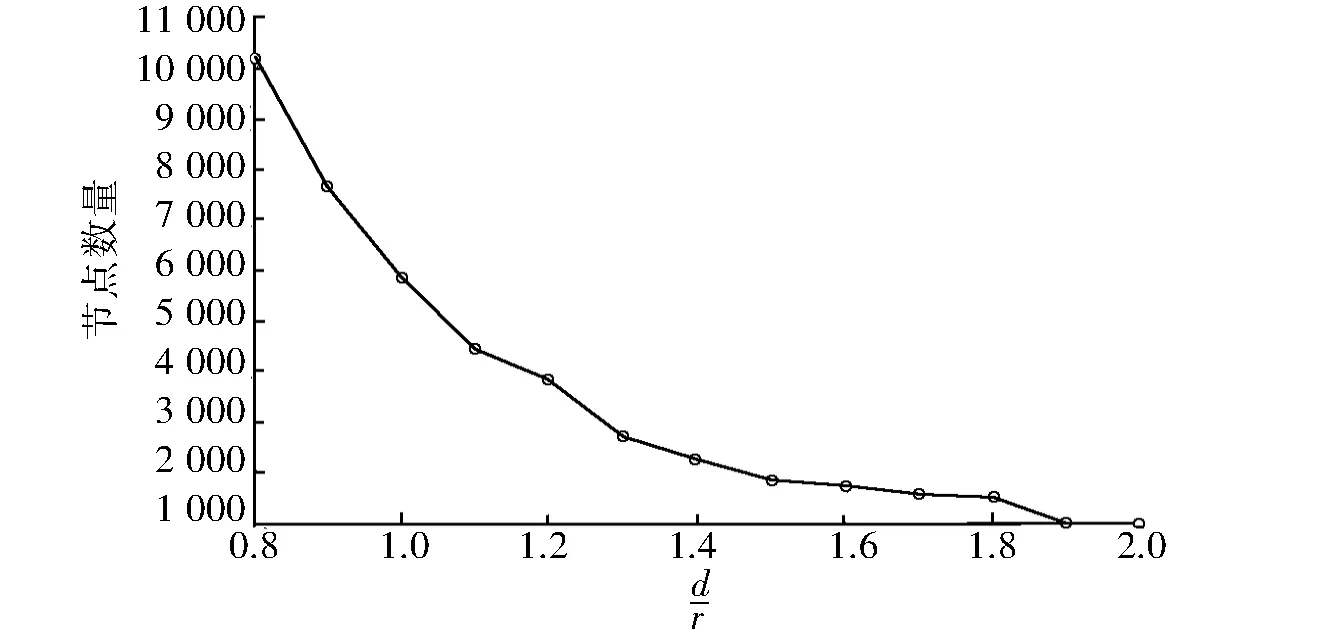
图2 节点数量mconn与的关系曲线Fig.
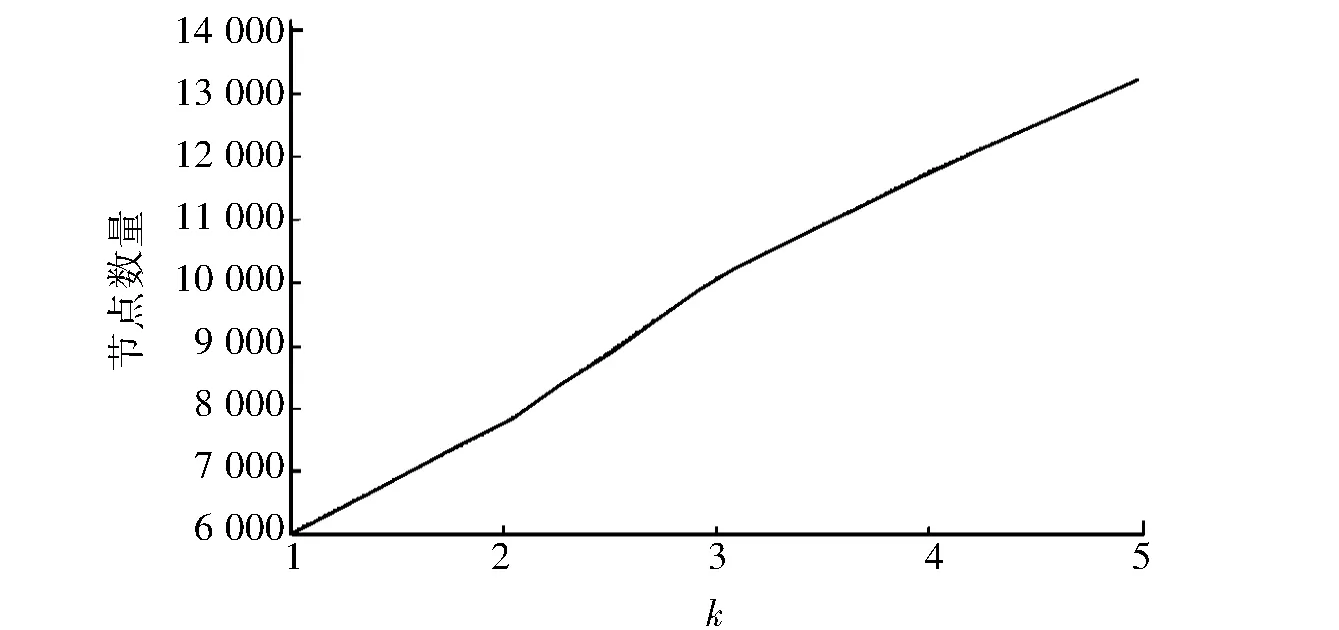
图3 节点数量mcover与k值的关系曲线Fig.3 Number of nodes mcover vs k
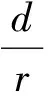
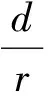

表与k,的关系表
4 结语
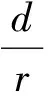
[1] ZHU C,ZHENG C,SHU L,et al.A survey on coverage and connectivity issues in wireless sensor networks[J].Journal of Network and Computer Applications,2012,35(2):619-632.
[2] ALAM S M,HAAS Z J.Topology control and network lifetime in Three-dimensional wireless sensor networks[J].Networking and Internet Architecture,2006(1):1-18.
[3] 钟永信,黄建国,韩晶.三维传感器网络部署、覆盖和连接问题研究[J].控制与决策,2011,26(10):1447-1451.
[4]POMPILID,MELODIAT,AKYILDIZIF.Three-dimensionalandtwo-dimensionaldeploymentanalysisforunderwateracousticsensornetworks[J].AdHocNetworks,2009,7(4):778-790.
[5] 凡高娟,王汝传,黄海平,等.基于容忍覆盖区域的无线传感器网络节点调度算法[J].电子学报,2011,39(1):89-94.
A calculation method of node demand in internet of things
HE Li, LI Bo
(CollegeofComputer,HenanUniversityofEngineering,Zhengzhou451191,China)
In Internet of Things (IOT) node comprehensive coverage and connectivity are related to whether the physical space can be effectively monitored. Coverage problem in two-dimensional space has been studied deeply. However, with the IOT applications extend into the air and water, coverage problem in 3D space needs to be solved. Since the recent methods of solvingk-coverage in 3D space are extended from the methods of solving 1-coverage, there are limitations. In summing up the current status of research on coverage problem, a novel and fast method was presented to calculate the node demand to meet thek-coverage conditions in 3d space. Exponential growth model is applied to find the sufficient value of node demand, and the divide-and-conquer strategy is used to quickly locate the necessary value of node demand. The experiments results show the adaptability of the new method is stronger and realistic.
k-coverage; divide-and-conquer strategy; coverage problem in 3D space
2016-11-18
河南省高等学校重点科研项目(17A520026);河南工程学院博士基金(D2012016)
何莉(1982-),男,江西萍乡人,讲师,博士,主要研究方向为物联网与智能计算.
TP311
A
1674-330X(2017)01-0057-05

