基于SIFT和RANSAC的鞋印图像匹配算法

董艳丽，崔 艳

(天津工业大学 理学院，天津 300387)

基于SIFT和RANSAC的鞋印图像匹配算法

董艳丽，崔 艳

(天津工业大学 理学院，天津 300387)

针对失真的鞋印图像的匹配问题，在研究中引入了基于尺度不变特征变换SIFT(scale-invariant feature transform)算法与RANSAC算法相结合的图像匹配方法.首先，对图像进行SIFT特征点的提取，在分析 SIFT 特征描述子生成的基础上，以最小欧式距离为标准来判断特征点是否匹配.然后，用最小欧式距离与次小欧氏距离之比进行初始匹配，用随机抽样一致性算法剔除SIFT算法匹配过程中存在的误匹配点对，从而实现精确匹配.实验结果表明，在局部鞋印图像中含有尺度缩放和旋转失真的情况下，该算法达到了良好的匹配精度且具有较强的鲁棒性和有效性.

鞋印图像；图像匹配；SIFT算法；RANSAC算法

鞋印是一种重要的物理证据，可以提供犯罪嫌疑人与犯罪地点之间的联系[1-2].相对于指纹，鞋印在犯罪现场很常见且容易获取，通过将犯罪现场的鞋印图像与鞋印数据库进行对比，可以获得非常有价值的案件侦破线索[3].在犯罪现场，由于环境的复杂性与地理特征的局限性，局部鞋印图像相对于完整的鞋印图像更容易提取.因此，研究局部鞋印在鞋印自动识别系统中具有重要的意义，而鞋印图像匹配作为鞋印自动识别系统中的重要内容，其匹配算法具有重要的研究价值[4-5].

图像匹配算法一般分为两种,一种是基于图像的某些区域的匹配算法，另一种是基于图像的局部特征点匹配算法,如尺度不变特征变换算法(Scale-invariant Feature Transform,SIFT)[6].该方法充分利用了图像灰度的统计特性，避免了由于局部环境、光照、噪声等造成失真引起的误匹配，对匹配图像的非本质变化不敏感，对含有尺度、旋转、噪声失真的图像匹配效果较好.在鞋印图像匹配的应用上，SIFT算子的总体性能优于其他算子，提取的特征点具有良好的几何稳定性，尤其适合图像存在较大变形的局部目标识别、 图像匹配等任务.SIFT算法对图像的缩放、旋转、位移等保持不变性，具有抗干扰能力强、稳定性好等诸多优点，被广泛应用于多个领域[7-9].

鞋印匹配的关键是克服所收集鞋印图像质量方面无法控制的问题，如背景、尺度缩放、旋转、噪声等由于非垂直拍摄而引起的失真[10-11].为了提取具有高稳定性、高匹配性的局部特征，解决局部鞋印的失真问题，本研究在原始SIFT算法[12]的基础上，利用随机抽样一致性算法(Random Sample Consensus，RANSAC)[13-14]对特征点匹配点对提纯，根据精确匹配的特征点数实现鞋印图像匹配的鲁棒性和有效性.

1 SIFT算法

1.1 检测尺度空间极值点

SIFT算法是在尺度空间中进行特征点检测的，不同尺度表示图像的不同特征.

图像的尺度空间定义为函数L(x，y，σ)，即具有尺度变化的高斯函数G(x，y，σ)与图像I(x，y)的卷积，生成图像的高斯金字塔LoG，如式(1)和式(2)所示：

L(x，y，σ)=G(x，y，σ)×I(x，y)，

(1)

(2)

式中：(x，y)代表图像像素坐标处的灰度；σ是空间尺度.采用高斯差分DoG(Difference of Gaussian)图像来获取图像的极值点，DoG为相邻尺度空间的函数之差，即

D(x，y，σ)=[G(x，y，kσ)-G(x，y，σ)]×I(x，y)=L(x，y，kσ)-L(x，y，σ)，

(3)

式中：k为乘性因子，是一个常数.

寻找尺度空间的极值点，每一个采样点需要和它所有的相邻点进行比较，采样点和它同尺度的8个相邻点及上下相邻尺度对应的9×2个相邻点共26个点进行比较，若该像素点的灰度值在这26个邻域像素中皆为极值，则为候选的极值点.

1.2 精确定位极值点的位置

为了获取稳定的特征点，采用拟合函数来实现空间极值点的精确定位，同时要去除低对比度的特征点和不稳定的边缘响应点，以增强匹配的稳定性，进而提高抗噪声能力.DoG函数在图像边缘有很强的边缘响应，利用Hessian矩阵剔除不稳定的边缘响应点，再次精确定位特征点的位置[15].

1.3 特征点方向的分配

为了使算子具备旋转不变性，通过梯度直方图确定特征点的主方向：

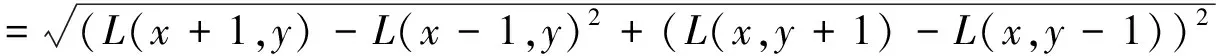
(4)

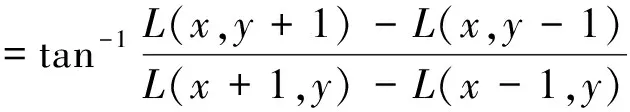
(5)

式(4)和式(5)分别为特征点处的梯度幅值和梯度方向的计算公式.每个特征点被指定有一个主方向，少许特征点有一个主方向和多个辅方向，以增强匹配的鲁棒性[16].

1.4 生成特征点描述子

为了确保旋转不变性，先将坐标轴旋转为特征点的方向.以特征点为中心在16×16的邻域内计算，将邻域分成4×4的子像素块，然后对子像素块计算8个方向的直方图.因此，每个特征点的特征描述符的特征向量是4×4×8=128维.

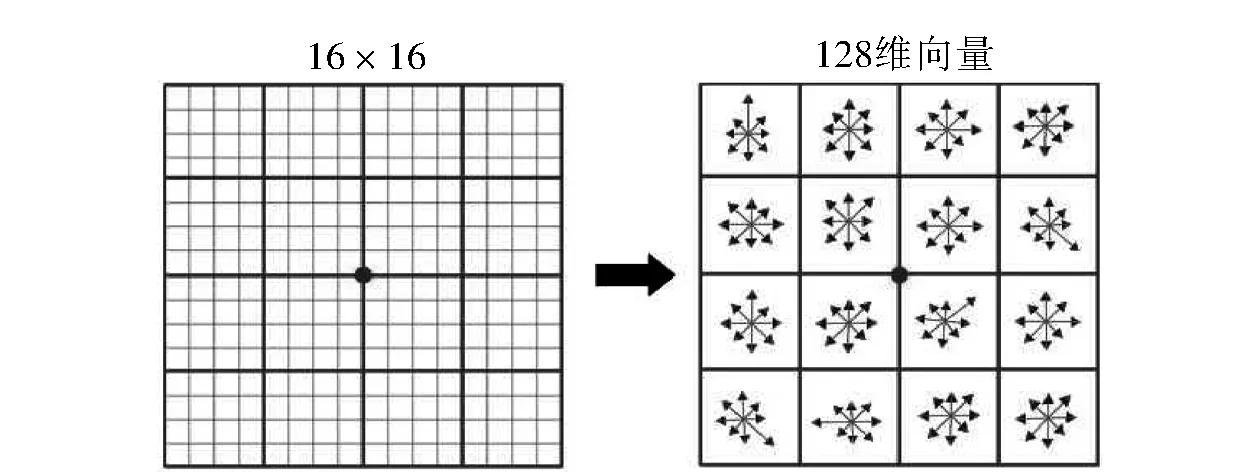
图1 SIFT描述子Fig.1 SIFT descriptor

SIFT特征向量除去尺度变化、旋转等几何变形因素的影响之后，归一化特征向量的长度，进一步除去光照变化的影响[17]，如图1所示.

2 随机抽样一致性算法

随机抽样一致性算法(RANSAC)是根据一组包含异常数据的样本集，通过假设计算出数据的数学模型参数，从而得到有效的样本数据的算法.RANSAC算法的基本假设是样本中包含正确数据(即可以被模型描述的数据)，也包含异常数据 (即无法适应数学模型的数据).为了得到最优的模型，需确定模型所需数据的最小集合.RANSAC算法的基本思想描述如下：

(1)从样本集P中随机选取一个最小抽样集，由这个子集初始化模型.

(2)找出根据阈值Td判断后成为当前模型的支撑点集S，集合S就是样本的内点.

(3)若集合S的大小超过了某个阈值Ts，用S重新估计模型并结束.

(4)若集合S小于阈值Ts，选取下一个新的样本，重复上述步骤；随机抽样计算N次，选出最大的一致集，重新计算模型，得到最后的结果.

3 特征点的匹配

当两幅图像的关键点特征向量生成后，采用关键点特征向量的欧式距离为两幅图像中关键点的相似性判定度量.取待匹配图像中某个关键点的特征向量，找出其与原始图像中欧式距离最近的前两个特征点，在这两个特征点中，如果最近邻的距离与上次近邻的距离的比值小于某个比例阈值δ(δ设定为0.8)，则接受这一对匹配点.

在匹配的过程中，会出现一些错误的匹配点对，可利用RANSAC算法将其剔除.首先，输入4个匹配点对数据，得到模型参数，利用此模型寻找其他局内匹配点，计算出符合模型的局内数据并重新计算模型参数作为下一个状态，迭代此过程.重复操作随机抽样计算N次，选择数目最多的局内点为最终局内点.确定一个适当的迭代次数M，确保4对匹配点都是局内点的概率为99%.RANSAC算法在剔除误匹配点的同时，计算匹配点在变换矩阵的正变换与逆变换后的误差，利用设置的阈值剔除误差较大的点，得到进一步精化的匹配点，以达到最佳的匹配效果.

4 实验和分析

采用MatlabR2015a来实现整个实验过程，评价指标是正确匹配率(CorrectMatchingRate，CMR)，即正确的匹配序列对数与总匹配序列对数的比值[18-19].

实验采用人工提取的鞋印图像进行测试，每个样本图像的磨损程度不同.从每幅样本图像中各截取4幅不同的局部鞋印图像，截取的局部图像分别为前脚掌、后脚跟、左半部鞋印与右半部鞋印，分别用P1～P4来表示.图像P1～P4均占原始鞋印图像的50%左右，样本图像尺寸为240像素×640像素.然后，对每个局部图像进行旋转和缩放失真，产生失真图像，从而构成测试数据库，如图2所示.

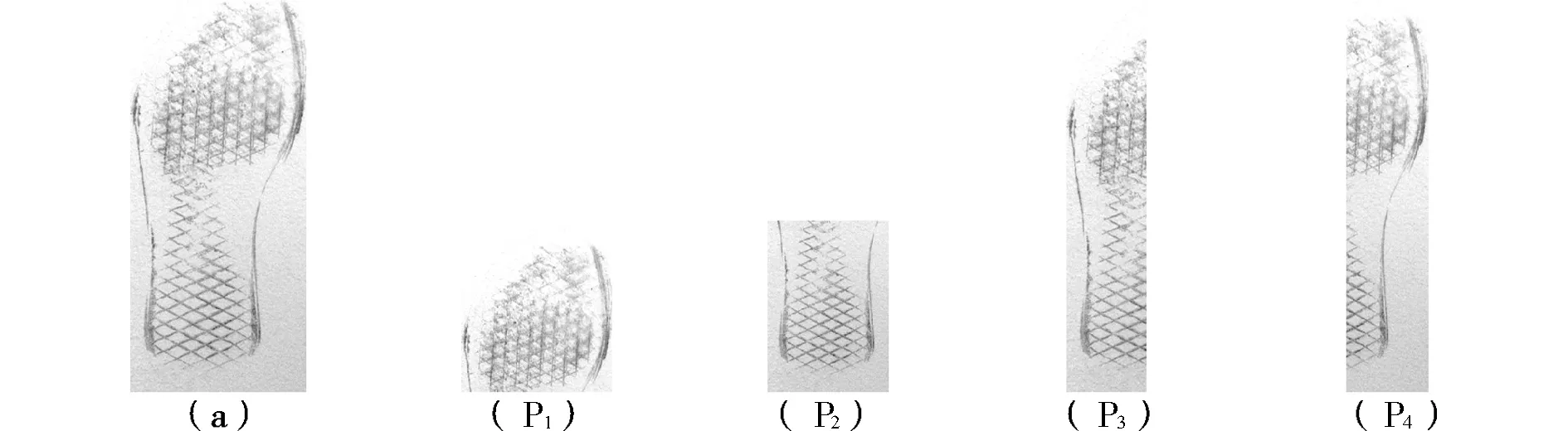
图2 测试数据库Fig.2 Test database

实验采用的样本待匹配图像如图2(a)所示，样本图像中待匹配目标如图2(P1)～(P4)所示.首先，进行SIFT特征点提取，之后检测出图像的匹配点对，利用RANSAC算法筛选出全部正确的匹配点对，实验结果如图3和表1所示.从表1可知，鞋印局部图像P1～P4与样本图像的正确匹配率为98%～100%，匹配精度较高.同时，对P1～P4这4组局部图像增加随机旋转和缩放失真，再次组成测试图组.表2和表3为测试数据库中4组局部鞋印图像在不同质量下的实验结果.表2的数据显示，旋转失真后的图像P1～P4与样本图像的正确匹配率为71%～86%；表3的数据显示，缩放失真后的图像P1～P4与样本图像的正确匹配率为91%～96%.由此可知，SIFT与RANSAC相结合的算法处理鞋印图像能达到较高的匹配精度，对存在旋转和尺度失真的鞋印图像具有一定的有效性.

图3 局部鞋印图像匹配结果Fig.3 The matching result of partial shoeprints image

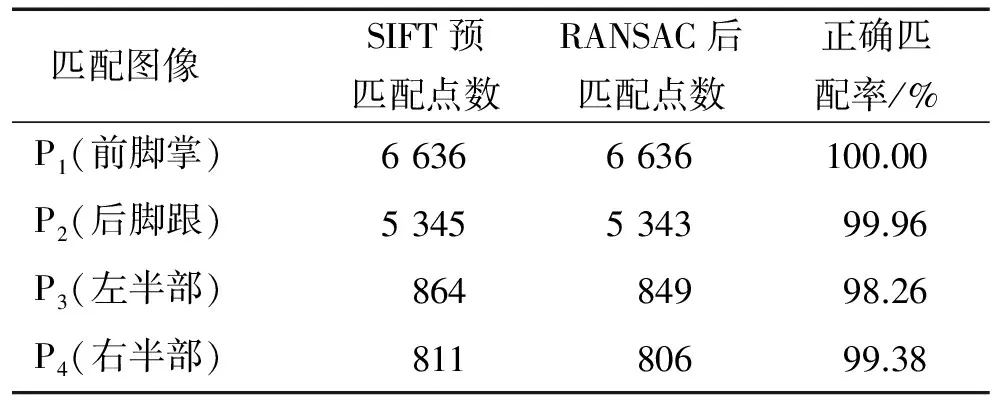
匹配图像 SIFT预匹配点数RANSAC后匹配点数正确匹配率/%P1(前脚掌)6636 6636 100．00P2(后脚跟)5345 5343 99．96P3(左半部)864 849 98．26P4(右半部)811 806 99．38

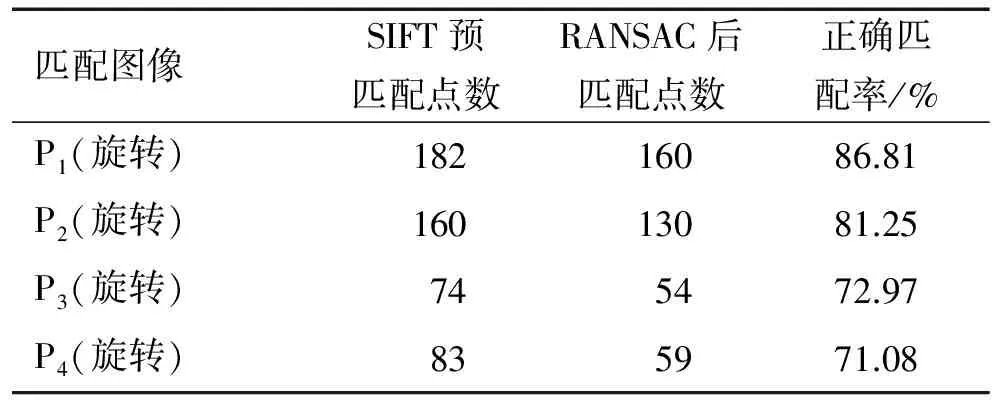
表2 P1～P4旋转失真图像SIFT算法和RANSAC算法相结合的实验结果

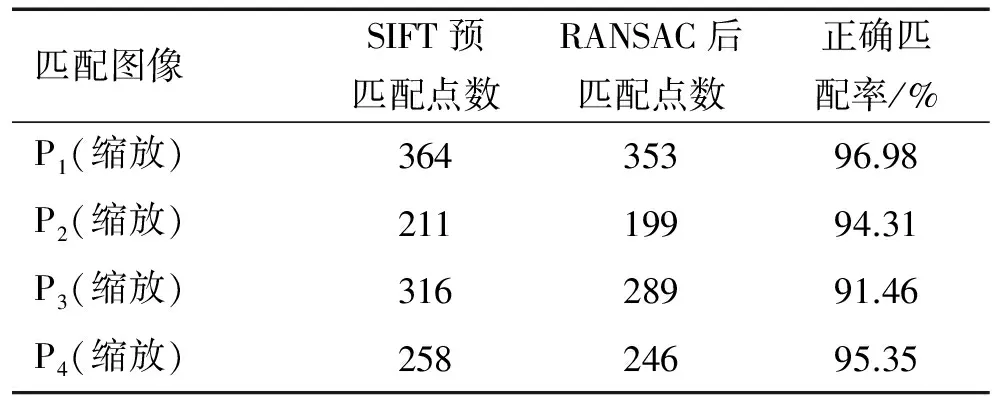
表3 P1～P4缩放失真图像SIFT算法和RANSAC算法相结合的实验结果

为了测试本算法的鲁棒性和有效性，避开随机性带来的误差，取10幅样本图像，共120幅局部图像组成测试数据库.对测试数据库进行实验，得出不同局部鞋印图像匹配精准度的对比曲线，如图4所示.

由图4可以看出，本实验用SIFT算法预匹配和RANSAC算法去除误匹配后，得到的正确匹配率均在70%以上.图4(a)中，该算法的正确匹配率为75%～100%；图4(b)和(c)是对旋转和缩放图像的实验结果，该算法的匹配精度为70%～95%，增加旋转和缩放失真的图像对其匹配精度没有太大的影响.这就证明了SIFT和RANSAC相结合的算法对存在尺度和旋转失真的图像的匹配有一定的不变性，利用图像的局部特征点对来完成模板匹配，匹配的精准度较高.

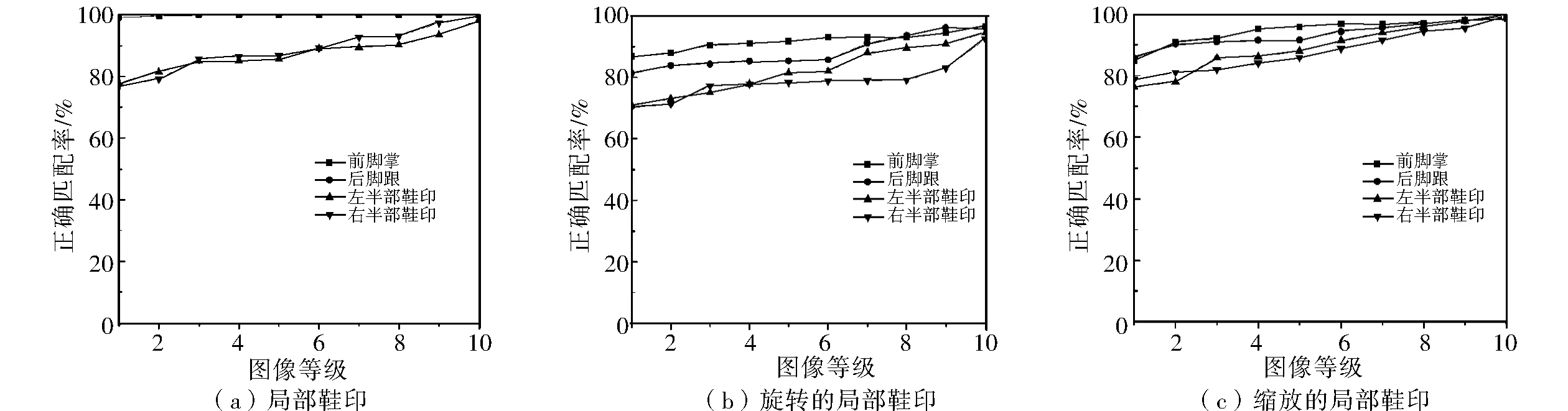
图4 不同质量鞋印图像的正确匹配率Fig.4 The correct matching rate of partial shoeprints in different qualities

由图4(a)可知，无论局部鞋印的质量如何，利用本方法进行匹配，前脚掌和后脚跟图像的正确匹配率均为95%～100%，左右局部图像的正确匹配率均为75%～100%.这是因为一些左右两部分鞋印图案在纵向分割时，鞋印的图案被破坏，局部特征发生了变化，影响了特征点的提取.而横向切割的鞋印图像如前脚掌和后脚跟，相对于左右局部图像保存了鞋印图案的完整性，保留了大部分信息，故提取的特征点数目较多.

从上述实验结果可知，利用本匹配算法进行鞋印的局部特征点模板匹配，鞋印图像的前脚掌和后脚跟区域要优于左右局部鞋印图像的匹配精度，多数特征点的匹配受图像失真的影响较小.

5 结语

将SIFT算法和RANSAC算法结合，提出的鞋印匹配方法充分利用SIFT特征与RANSAC算法的鲁棒性，有效地解决了存在旋转和尺度失真的图像的匹配问题，具有较高的匹配精确度，未来的研究工作是提高匹配效率的同时保持匹配效果不变.

[1] BODZIAK W J.Footwear Impression Evidence-Detection,Recovery and Examination[M].Boca Raton：CRC Press LLC,2000.

[2] THOMPSON T,BLACK S.Forensic Human Identification:an Introduction [M].Boca Raton：CRC Press,2007.

[3] CHAZAL P D,FLYNN J,REILLY R B.Automated processing of shoeprint image based on the fourier transform for use in forensic science [J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2005,27(3):341-350.

[4] ALGARNI G,HAMIANE M.A novel technique for automatic shoeprint image retrieval [J].Forensic Science International,2008,181(1/3):10-14.

[5] TAPIO L,ANTTI L.Measuring the accuracy of automatic shoeprint recognition methods [J].Journal of Forensic Sciences,2014,59(3):1-7.

[6] DAVID G L.Object recogniton from local scale-invariant features[J].The Proceedings of the International Conference on Computer Vision,1999(2):1150-1157.

[7] RAJEEV R,KH M S.Digital Image forgery detection using SIFT feature [J].International Symposium on Advanced Computing and Communication,2015(4):186-191.

[8] TONY L.Image matching using generalized scale-space interest points [J].Journal of Mathematical Imaging and Vision,2015,52(1):3-36.

[9] CHEN Y,SHANG L.Improved SIFT image registration algorithm on characteristic statistical distributions and consistency constraint[J].Optik,2016,127(2):900-911.

[10]SHEIDA H,RIAN M S,JOHN B.The interpretation of shoeprint comparison class correspondences [J].Science and Justice,2012,52(4):243-248.

[11]ALMAADEED S,BOURIDANE A,CROOKES D,et al.Partial shoeprint retrieval using multiple point-of-interest detectors and SIFT descriptors [J].Integrated Computer-Aided Engineering,2015(22):41-58.

[12]LOWE D G.Distinctive image features from scale-invariant keypoints [J].International Journal of Computer Vision,2004,60(2):91-110.

[13]FISCHLER M A,BOLLES R C.Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography [J].Communications of the Association for Computing Machinery,1981,24(6):381-395.

[14]CHALOM E,ASA E,BITON E.Measuring image similarity:an overview of some useful applications [J].IEEE Instrumentation & Measurement Magazine,2013,16(1):24-28.

[15]AHROR B,DJAMAL B.A new generalised α scale spaces quadrature filters [J].Pattern Recognition,2014,47(10):3209-3224.

[16]LIAO K,LIU G Z,HUI Y S.An improvement to the SIFT descriptor for image representation and matching [J].Pattern Recognition Letters,2013,34(11):1211-1220.

[17]YIU Y,LIU S P,WANG Z F.Multi-focus image fusion with dense SIFT [J].Information Fusion,2015(23):139-155.

[18]PRADEEP M P,JAYANT V K.Rotation and intensity invariant shoeprint matching using Gabor transform with application to forensic science [J].Pattern Recognition:the Journal of the Pattern Recognition Society,2009,42(7):1308-1317.

[19]KHAN M A,ANSARI M B.Rotation invariant matching of partial shoeprints [J].International Journal of Engineering Research and Applications，2014,4(9):1-5.

An approach to the partial shoeprints image matching based on SIFT and RANSAC

DONG Yanli, CUI Yan

(SchoolofScience,TianjinPolytechnicUniversity,Tianjin300387,China)

This paper presents a solution for the matching of shoeprints which is considerably more robust than existing solutions in the presence of geometric distortions such as scale, rotation distortions. A new matching method is proposed based on SIFT and RANSAC algorithm. Firstly, feature detection and pre-matching of images are done by using SIFT algorithm. Then we applied the matching between the extracting interest points descriptor with a nearest neighbor method using the Euclidean distance. Secondly, the mismatching is wiped out by using RANSAC algorithm. This method solves the mismatching problem of image matching. Experimental results show that compared with conventional algorithms, the proposed algorithm is more robust while maintaining good registration accuracy when analyzing partial shoeprint images in the presence of geometric distortions such as scale, rotation distortions.

shoeprint image; image matching; SIFT algorithm; RANSAC algorithm

2016-08-29

董艳丽(1988-)，女，山东菏泽人，硕士研究生，主要研究方向为图像匹配.

崔艳(1963-)，女，天津人，副教授，硕士生导师，主要研究方向为图像处理与模式识别.E-mail:cuiyan@tjpu.edu.cn.

TP391.7

A

1674-330X(2017)01-0071-05