线板式静电除尘器数学模型的建立及数值仿真
李永兵, 曾 珠, 李兵磊
(1.河南工程学院 安全工程学院 ,河南 郑州 451191;2.福州大学紫金矿业学院 采矿工程系,福建 福州 350108)
线板式静电除尘器数学模型的建立及数值仿真
李永兵1, 曾 珠1, 李兵磊2
(1.河南工程学院 安全工程学院 ,河南 郑州 451191;2.福州大学紫金矿业学院 采矿工程系,福建 福州 350108)
简要介绍了线板式静电除尘器除尘过程中所发生的各种物理现象,在前人所建立的数学物理模型的基础上,通过对静电除尘器中高压静电场、气流场和电力场的分析,建立了粉尘粒子输运的数学模型,修正了以前理论中不合理的边界条件,重新建立了静电除尘器实际除尘规律的新的边界条件,建立了除尘电场模型、尘粒荷电模型、粉尘颗粒捕捉等一系列反映静电除尘过程的数学物理模型.运用差分法对静电除尘器的数学模型进行求解,利用Matlab和Fortran进行数值模拟算法设计和方程求解,得到了静电除尘器中粉尘粒子在高压静电场中的浓度分布和运动规律.利用所建立的实验模型对本研究数值模拟的结果进行验证,可知建立的数值模型和边界条件基本符合静电除尘器的除尘规律.
静电除尘器;数学模型;粉尘粒子;数值仿真;除尘效率
随着现代工业的高速发展与人们环境保护意识的进一步加强,静电除尘技术也有了长足的进步.在理论方面,文献[1]对著名的Deutsch-Anderson公式进行了阐述.后来,之后的研究者又针对研究中所发现的非Deutsch现象从不同角度提出了Deutsch公式的修正式.随着静电除尘理论研究的进一步深入和计算机技术的飞速发展,人们对静电除尘的机理有了更深层次的研究.尽管静电除尘的过程仅包括粉尘荷电、捕集和清灰3个部分,但是各环节受众多因素的影响和制约,对过程中所发生的一切复杂的现象很难用一个统一的除尘效率理论进行描述,所以除尘效率理论的发展有待于高压静电场理论和紊流理论的进一步发展[2].借助于建立在计算机基础上的静电除尘器数学模型,不但可以定性定量地了解电除尘器的机理,模拟静电除尘器中所发生的过程,了解因为某个或者几个参数的改变所引起其他参数的变化趋势,而且还可以借助于数学模型对实验结果进行分析和总结,利用已有的数据对实验进行必要的推断,可以节省大量的人力、物力和财力,特别是对于那些只能做少量实验或者只能获取少量数据的情况,作用会更加明显.
1 数学模型的建立
建立静电除尘器数值研究的方法一般都是从电的参数的计算、粒子荷电的计算、理想效率的计算及非理想因素的校正这4个方面着手,通过综合这几方面的研究成果来建立数学模型[3].本研究也是采用此方法建模,思路为利用尘粒荷电方程来确定尘粒所带的电量,然后由电场方程和离子守恒方程组合确定除尘器的电场空间中某一个位置的电场强度.由尘粒所带电量和当时的电场强度来确定尘粒动量方程中所受到的电场力的大小,然后通过耦合气体的质量和动量守恒方程就可以求出尘粒在空间中某一个时刻和某一个位置的速度及尘粒的浓度.因此,通过求出除尘器气流入口和出口的尘粒浓度就可以最终确定静电除尘器的净化效率.
线板式静电除尘器的除尘过程主要包括电场分布、尘粒荷电、尘粒迁移和尘粒收集[4]这4个部分,为了能够尽可能完整地描述静电除尘器的除尘过程,数学模型被分为以下4个部分来考虑:静电除尘器中电场的分布及尘粒荷电、粒子输运方程的建立、尘粒的分布和收集、除尘过程中的其他现象.
1.1 电场分布
线板式静电除尘器两极间的电场有3种功能:第一,它会在电极附近产生电晕现象,在强电场的作用下能够产生大量的荷电离子;第二,电场能够提供使电荷传递给尘粒的荷电离子驱动力;第三,产生收集粉尘尘粒所需要的电场力.静电除尘器内部的电场分别受到由电压作用在电极系统上所形成的表面电荷和极板间离子及荷电尘粒所形成的空间电荷这两种因素的共同影响[5].
对于线板式电除尘器来说,由于各种因素的存在,计算其电场强度较为困难[6].然而,工业中所使用的大部分静电除尘器都是基于线板式的.因此,对于建立线板式静电除尘器内部电场的数学模型就显得特别重要.
在稳定的情况下,电场的一般形式可以使用如下的控制方程来表示:
·(Eε0)=ρ.
(1)
电流连续性方程:
·J=0,
(2)
式(1)和式(2)中:E=-V,其中V为空间电位;ε0为自由空间介电常数;ρ为空间电荷密度;J=ρbE,其中b为电荷载体迁移率.
式(1)可以转换成泊松方程的形式:
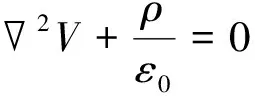
(3)
即
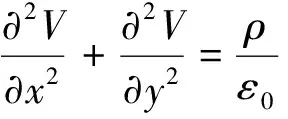
(4)
在静电除尘器的工作过程中,施加在放电极线上的电压V0还没有达到电晕电压时,两极板间并不会出现电晕现象,也就不会存在离子,此时ρ=0.
而电场的拉普拉斯方程为
2V=0.
(5)
在二维直角坐标系下,方程式(5)可以表示为离散方程的形式:
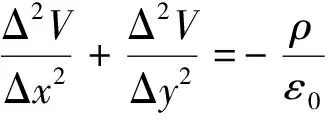
(6)
由式(1)、(2)和(4)组成方程组并解得
·J=ρb(·E)+ρ(E·b)+b(E·ρ)=·(ρbE),
(7)
即
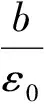
(8)
1.2 尘粒荷电
为了计算静电除尘器内的尘粒荷电量,必须确定它内部的电场分布.对于电场荷电来说,主要的影响因素是尘粒的半径r、电晕场中的荷电场强E0和相对介电系数ε.
半径为r的尘粒荷电量qi与时间变化的关系式如下:
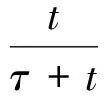
(9)
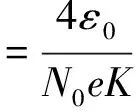
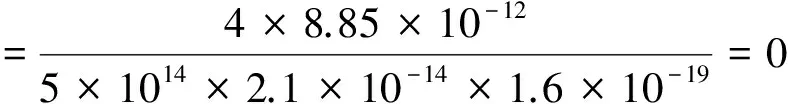
(10)
当荷电时间t为0.02 s时,尘粒将达到90%以上的荷电率,这个时间基本可以认定尘粒已经完成了荷电过程,也就是说尘粒荷电的过程是在一个很短的时间内完成的,所以尘粒的电场荷电时间与尘粒在除尘器内部的停留时间相比可以忽略不计.
1.3 粒子输运方程的建立

图1 静电除尘器电场及所取微元体Fig.1 Electrostatic field of electrostatic precipitator and schematic diagram of micro-element
荷电粒子在高压静电场中的运动是一个极其复杂的物理过程,它主要受流场、静力场、重力场和扩散场的影响.荷电粒子是在这些场的共同作用下进行沉降的[7].
为了建立粉尘粒子运动的数学物理方程,做如下假设:在电场空间中设定三维坐标,坐标的原点位于进口截面的中心,气流的方向定为x轴,电晕极线到收尘极板的方向定为y轴,重力的方向为z轴,如图1(a)所示.在此三维坐标系中取一个微元体,如图1(b)所示.
假设这个微元体在x,y和z方向上的长度分别为dx,dy和dz.在实际应用中,粉尘粒子受重力的影响比受气流和驱进速度的影响要小很多,可以忽略不计,可得粉尘粒子的二维平面模型方程:
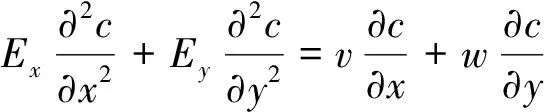
(11)
1.4 边界条件的建立
用数学模型来描述现实中的一些规律,如果不是同一个问题,即使所用的数学模型相同,最后解出的答案也是不同的.即使对于同一类问题且有着相同的数学模型,但由于假设的边界条件不一样,最后解出来的答案也可能是不一样的.
为了求解前面建立的静电除尘器的数学物理模型,必须要建立边界条件,现做如下假设:
(1)静电除尘器入口的粉尘颗粒浓度是均匀的,设为c0,即c=c0,y=0.
(2)假设除尘器的收尘极板是长的,那么在除尘器出口处的粉尘浓度为0,即c=0,y→∞.
(3)电晕线平行排列且平行于收尘极板,因为在x方向上的电场强度为Ex,理论值为0,所以在这个平面上沿x方向运动的粉尘粒子的输运为0,用数学方程表示为
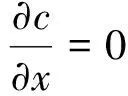

根据以上假设的4个边界条件,可得到完整的静电除尘器的粉尘粒子输运数学物理模型:
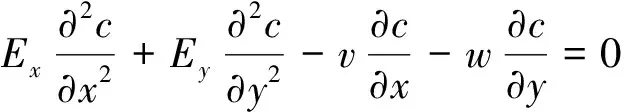
(12)
边界条件为
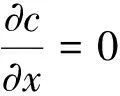
1.5 数学模型的编程算法描述
求解所建立的静电除尘器数学模型的有限差分方程,算法描述如下:
(1)根据放电极线上的电位初值,利用Cooperman方程计算静电除尘器收尘电场空间中每一节点处的电位分布.
(2)根据建立的有限差分格式方程计算出电场空间中每一节点的电荷分布值及极线上的空间电荷密度分布值.
(3)根据输入的参数并根据有限差分格式解出泊松方程,然后计算电场中每一处节点的电位分布.
(4)重复第(2)步和第(3)步,直到电场的电位差和空间电荷的密度差达到收敛.
(5)计算除尘极板上的平均电流密度并与实验值(或实际测量值)比较,如果误差在3%之内,即满足收敛的要求,可以认为计算结束.否则,需要重新调整参数,重复以上步骤,直到满足收敛的要求.
2 实验模型的建立
为了验证数值计算的结果,根据静电除尘器的机理设计制作了一个基本能反映除尘器实际情况的双通道实验室用静电除尘器模型,电除尘器的放电电极均匀地放置在两块收尘极板之间.模型的尺寸如表1所示,外形结构如图2所示.实验中所用的高压电源为CK10MA/100kVA,电源的最大输出电压为125kV,最大输出电流为10mA,除尘器的电压和风速均可以调节.
由于滑石粉具有润滑、抗黏、助流、耐火、抗酸、绝缘、熔点高、化学性不活泼、遮盖力良好、柔软、光泽好、吸附力强等优良的特性,所以本实验中所用的粉尘采用滑石粉,风速控制在1m/s左右,然后将每块收尘极板自上而下依次平均划分成400mm×250mm大小的4份,将这4个区域分别标上序号1#,2#,3#,4#.收尘器工作一段时间后,将位于中间的收尘极板小心地取出,收集每份极板上沉积的粉尘并称其质量.
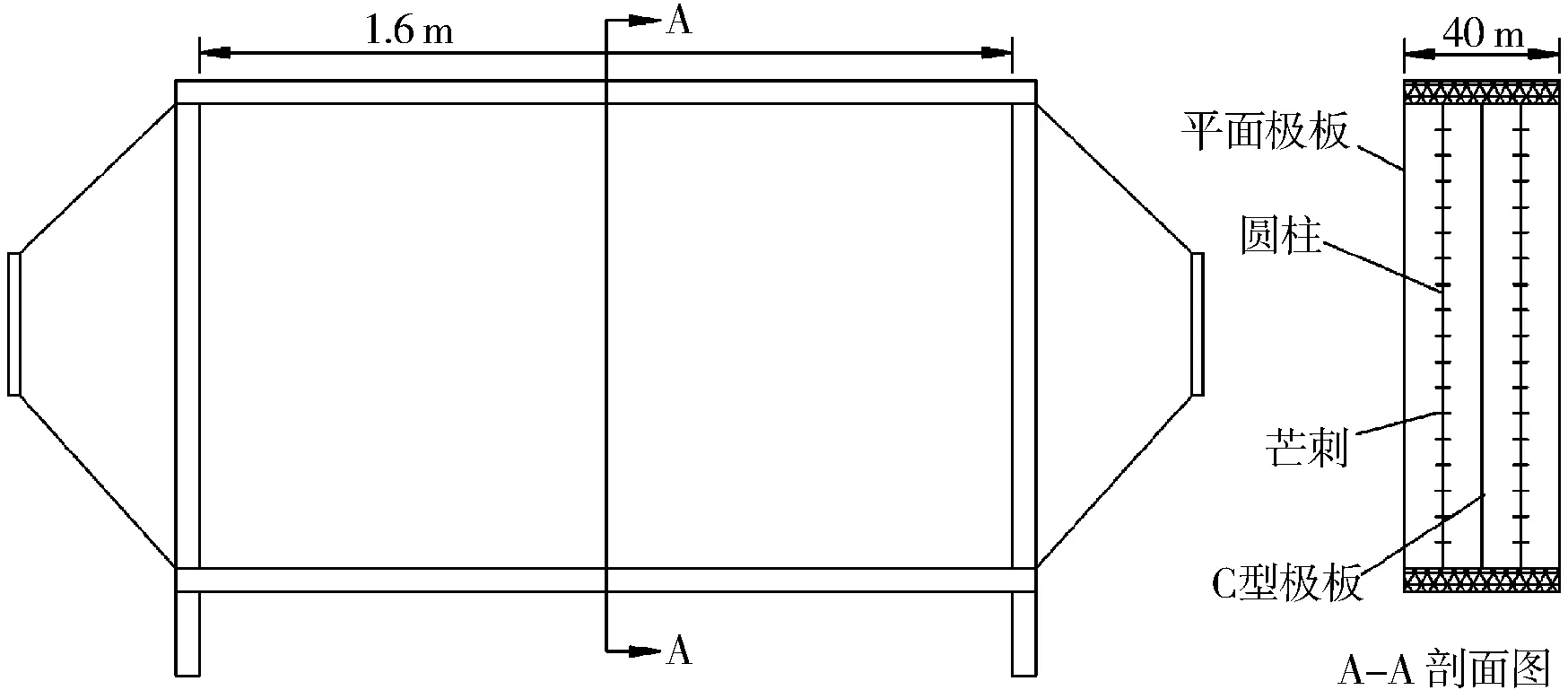
图2 电除尘器外形结构Fig.2 Electrostatic precipitator outline structure diagram
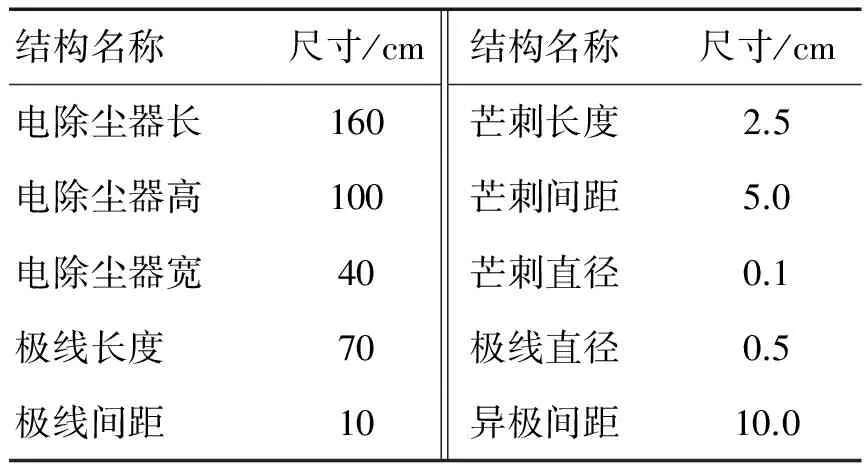
结构名称尺寸/cm结构名称尺寸/cm电除尘器长160芒刺长度2.5电除尘器高100芒刺间距5.0电除尘器宽40芒刺直径0.1极线长度70极线直径0.5极线间距10异极间距10.0
3 实验结果分析
电除尘器的每块收尘极板上不同高度的粉尘分布规律如图3所示.从上到下,粉尘沉积量是由少到多分布,沉积厚度是由薄到厚分布,而且变化比较大.同时也可以看出,极板从第1到第3区域上的粉尘呈现沉积量由少到多、沉积厚度由薄到厚的规律;但从第3到第4区域,极板上的粉尘所呈现的规律是沉积量由多到少、沉积厚度由厚到薄,但是粉尘沉积量的变化不是很大.
沿气流方向,不同收尘极板上沿积粉尘的分布见图4,收尘极板标号为一、二、三、四.由图4可知,绝大部分粉尘沉积在了第一块收尘极板上,沿气流方向,粉尘的沉积量是按由多到少、沉积厚度由厚到薄分布的.同时,用目测法也可知,沿着气流方向,每块极板上的粉尘也呈现由厚到薄的沉积规律.
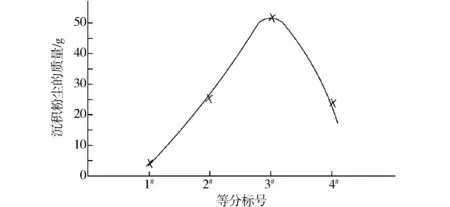
图3 沿气流方向,收尘极板不同高度沉积粉尘的分布Fig.3 Dust distribution along the air flow direction, collecting dust plate at different heights on the deposition
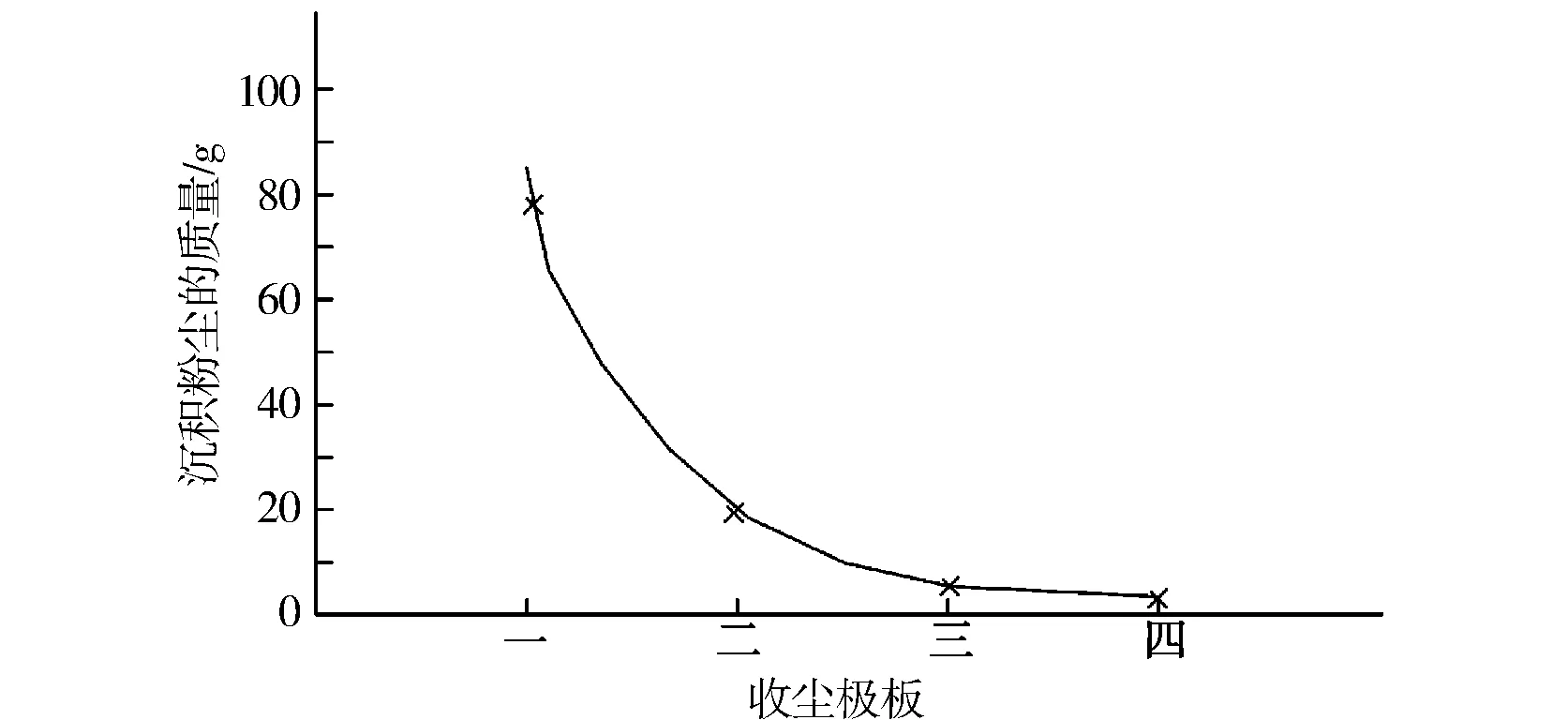
图4 沿气流方向,不同收尘极板上沉积粉尘的分布Fig.4 The distribution of dust on different collector plates along the airflow direction
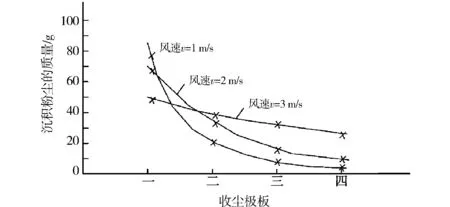
图5 风速不同时,收尘极板上沉积粉尘的分布Fig.5 When the wind speed is different, the deposition of dust on the dust collecting plate is distributed
风速不同时,收尘极板上沉积粉尘的分布见图5.从图5可以看出,当风速发生变化时,粉尘的沉降量会随着距离的增加而迅速减少,但在风速较高时,变化的幅度不是很大.这是因为,含尘气体中的粉尘颗粒大小并不是均匀单一的,含尘气体由气流速度较高的除尘器进口管通过喇叭口进入电场,气流速度会随之降为1 m/s左右,大小不一的尘粒就会呈现不同的沉降规律.
4 结语
从数值模拟和实验的结果对比来看,模拟值要比实验值高,这主要是因为在实验中会受到很多因素的影响,如粉尘颗粒的半径、介电常数,所处理气体的成分、黏度、压力、温度和密度,气体中所含各种成分的分子量,给粉尘粒子荷电的场强,工作电压、电流及除尘器的临界电压、临界场强,电晕线表面的光滑程度,除尘器的板间距,电晕线线距,电晕线半径等.这些都是建立数学模型必须要考虑的内在因素.还有一些外在因素没有考虑在建立数学模型的范围之内,如粉尘的黏结性、密度和它本身的附着力,气体的含尘湿度,粉尘的比电阻,电除尘器在工作时的稳定性,电晕闭塞和反电晕现象,电风效应,电场的配置特点,电场的风速,电极结构的性能,电风的影响,气流的均匀分布程度等.
由静电除尘器的基本理论可知,线板式静电除尘器内部粉尘粒子浓度的分布规律如下:在电晕线方向,粒子的浓度呈指数函数形式,并且是衰减的;在收尘极板附近也呈指数分布,不过是指数递增的.从实验结果来看,静电除尘器入口处横截面上的浓度变化是比较明显的,而出口处的浓度变化却不是很明显.产生这种现象的原因主要是因为静电除尘器是一种除尘效率很高的除尘净化装置,粉尘微粒在进入静电除尘器后不久就会在电场力的作用下沉降.
[1] LEONARD G L,MITCHER M,SELF S A.Experimental study of the effect of electro hydro dynamics flow in electrostatic precipitators[J].Fluid Mech,1983,127(2):123-410.
[2] 韦军新.浅谈静电除尘技术的研究发展[J].广西大学学报(哲学社会科学版),2000,22(12):193-195.
[3] 向晓东,陈旺生,刘新敏,等.长芒刺电除尘器性能研究[J].环境科学与技术,1999(1):4-7.
[4] 郝吉明,贺克斌,晁红勋,等.电除尘器数学模型的研究[J].清华大学学报(自然科学版),1989,29(3):95-104.
[5] 刘后启,林宏.电收尘器.理论设计使用[M].北京:中国建筑工业出版社,1987.
[6] 肖福春.宽间距电除尘器粒子收集特性[J].南方冶金学院学报,1993,14(3):197-205.
[7] 唐敏康.高压静电场中粉尘粒子的电气性能[M].北京:化学工业出版社,2010.
Research on mathematical model and numerical simulation of electrostatic precipitator with wire-plate
LI Yongbing1, ZENG Zhu1, LI Binglei2
(1.CollegeofSafetyEngineering,HenanUniversityofEngineering,Zhengzhou451191,China;2.CollegeofZijinMining,FuzhouUniversity,Fuzhou350108,China)
In this paper, the various physical phenomena in the process of wire-plate electrostatic precipitator are briefly introduced. Based on the mathematical physics models established by previous researchers, the electrostatic field, air flow field and electric field in electrostatic precipitator are analyzed, The mathematical model of dust particle transport is established, and the unreasonable boundary condition is corrected. Based on the original theory, the new boundary condition of electrostatic precipitator is deduced and the dust field model is established. Charge model is constructed, including dust particle capture and a series of mathematical models of the reaction process of electrostatic dust removal. The mathematical model of the electrostatic precipitator is solved by the difference methods, and the numerical simulation algorithm and the equation are solved using Matlab and Fortran. The concentration distribution and the movement law of the dust particles in the electrostatic field were obtained. The experimental results show that the numerical model and the boundary conditions are basically consistent with the dedusting rule of the electrostatic precipitator, which is verified by the established experimental model.
electrostatic precipitator; mathematical model; dust particles; simulation; collection efficiency
2016-10-20
李永兵(1980-),男,河南周口人,讲师,博士,研究方向为采矿工程.
X701
A
1674-330X(2017)01-0028-05

