运用“三十六计”，巧解小学数学习题

张丽云

摘 要：“三十六计”是根据中国古代汉族军事思想和丰富的斗争经验总结而成的兵书。在小学数学解题中运用“三十六计”，能够让学生形成一定的解题技巧，进而凸显数学中的问题解决策略，从中还可以窥见数学的思想方法。因此“三十六计”对于小学数学解题来说具有很强的实用性、针对性和指导性。

关键词：三十六计；小学数学；解题技巧

“三十六计”共分六套，即胜战计、敌战计、攻战计、混战计、并战计和败战计，“三十六计”相传为檀道济所辑，是古代汉族兵家计谋的总结和军事谋略学的宝贵遗产。

“他山之石可以攻玉”，在儿童数学学习中，运用“三十六计”，能够化抽象为形象，进而凸显数学的思想方法。下面结合自己的教学实践略举几个例子，以期抛砖引玉，求教于方家。

一、擒贼擒王

顾名思义，擒贼擒王是指擒拿敌军首领，打垮敌人主力，让敌人陷入群龙无首的混乱状态，进而彻底击溃对方。将擒贼擒王计策用在数学解题中，就是指要抓住题目的关键句、关键题眼、字眼，通过突破关键点来理顺数量关系，进而顺利解题。这里的关键点就是“贼王”，抓住它，问题的解决就能水到渠成。

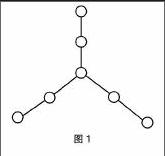
例1：如图1，将1～7分别填入图中的○内，使每条线段上三个○内数的和相等。

分析：解决此类问题的关键在于找到一个突破口。通过观察，我们不难发现，中间的一个圆圈是三根线交汇的地方，其他的圆圈只在单独的一根线上。那么，三根线交汇意味着什么呢？意味着中间圆圈中的数使用了三次，而其他圆圈中的数只使用了一次。因此，抓住中间圆圈中的数（贼王），也就算是牵住了“牛鼻子”。这里，我们不妨一一尝试。如果中间的圆圈里填上数1，那么三条线上的数之和为：1+2+3+4+5+6+7+1+1=30，所以每条线上三个圆圈中的数之和为：30÷3=10。由于中间的圆圈填上了1，所以每条线上另外两个圆圈中所填数之和为10-1=9。接着我们可以两两配对，分别是2和7，3和6，4和5。同理，中间圆圈除了可以填1外，还可以填4和7。因此，本题有三种填法。

二、无中生有

“无中生有”计策运用在军事上指运用假象欺骗对方，但却不是一假到底，而是要巧妙地由假变真，由虚变实，以各种假象掩盖真实情况，造成敌人的错觉，出其不意地打击敌人。将“无中生有”运用在数学解题中，就是要善于运用假设，从虚的数量关系中理出一个实在的具体数量来。由此化复杂为简单，达到解决问题的目的。

例2：水结成冰，体积增加10%，冰化成水，体积减少百分之几？

这里，“无中生有”所对应的数学思想方法就是“假设法”。假设法在数学解题中的运用十分灵活，经常在数学问题好像陷入“山重水复疑无路”的时候，让我们产生一种“柳暗花明又一村”的感觉。

三、欲擒故纵

所谓“欲擒故纵”，是指要想捉住他，可以故意放开他，让他放松戒备，充分暴露，进而将其捉住。正所谓“欲抑之，必先张之；欲擒之，必先纵之”。将“欲擒故纵”的计策运用到数学中来，即“以退为进”。正如著名数学家、统筹学的倡导者华罗庚先生所说，“善于退、足够的退，退到最原始而不失重要性的地方是学好数学的一个诀窍。”

四、围魏救赵

“围魏救赵”运用在军事上指让敌人分散兵力，歼灭敌人时不从敌人的正面进攻，而是从敌人的侧翼迂回出击。由于敌人的侧翼受到牵制，因此敌人的正面围困自然可以解除。从字面上看，“围魏救赵”即通过围魏而达到成功救赵的目的。在数学学习中，有时正向思考很难解决问题，为此我们可以从题目的侧面或反面展开思考，或许能够打开解题的另一扇窗。解题时，可以暂时避开题目的实点，从题目的虚点切入。

例4：李大妈家里有90个鸡蛋，并且还饲养了一只每天都会下蛋的老母鸡。李大妈有一个吃蛋的习惯，她每一餐都要吃1个鸡蛋，这样一天下来要吃3个鸡蛋。请你算一算，李大妈的鸡蛋能够吃多少天？

分析：这一道题类似于“牛吃草问题”。解决这样的问题有两个难点：一是原来有90个鸡蛋，二是一只老母鸡每天都在下蛋。如果我们直面习题本身，其列式将会非常麻烦。首先是原有的90个鸡蛋，能够让李大妈吃90÷3=30（天）。在这30天中，老母鸡又下了30个鸡蛋，可以让李大妈吃30÷3=10（天）。在这10天中，老母鸡又为李大妈下了10个鸡蛋，10÷3=3……1，能吃3天还剩余1个鸡蛋。这3天老母鸡又下了3个鸡蛋，连同前面剩下的1个鸡蛋，一共是4个鸡蛋，4÷3=1……1。这1天，老母雞生了1个鸡蛋，连同剩下的1个鸡蛋，合起来是2个鸡蛋，向别人借1个鸡蛋，一共是3个鸡蛋，3÷3=1（天）。老母鸡在这一天下了1个鸡蛋正好还给别人。这样李大妈的蛋一共能够吃：30+10+3+1+1=45（天）。但是当我们采用“围魏救赵”的解题策略另辟蹊径时，其解题思路将会更加敞亮。李大妈每天吃3个鸡蛋，其中的1个是老母鸡当天生的，相当于李大妈每天从原有的90个鸡蛋中吃2个鸡蛋，因此李大妈一共可以吃：90÷2=45（天）。

五、偷梁换柱

所谓“偷梁换柱”，就是指用偷换的方法，改变事物的内容、本质，从而达到自己的目的。“偷梁换柱”的计策用在数学解题中，就是指当我们遭遇到繁杂的问题例如计算题时，可以运用字母或设参数来简化习题，以便让题目中的关系更显明，从而达到解决问题的目的。

例5：计算：20152016×20162015-20152015×20162016。

分析：本题是一道计算题，题目中的数非常大，但是又存在着一定的规律，那就是题目中的数非常工整。通过观察，我们不难发现被减数中的两项和减数中的两项分别大1或少1。为此我们尝试设定参数，用“偷梁换柱”的策略简化习题表达。设A=20152015，B=20162015，那么原题我们可以用字母来表达：（A+1）B-A（B+1）

=AB+B-AB-A

=B-A

=20162015-20152015

=10000

六、声东击西

“声东击西”从字面的意思来解释就是佯攻东，实攻西。将“声东击西”用在军事上指通过假动作欺骗敌方，掩护主力在第一时间击其要害，进而达到出奇制胜的一种计策。将“声东击西”的策略运用到数学解题的过程中，就是要打破思维的习惯，突破一般的解题思路和常规的解题思维。在数学解题过程中，有时按部就班是不能解决问题的，必须通过自己的思考从另一个角度入手，开辟解题新思路。

例6：已知一个正方形的面积是60平方厘米，在这个正方形内画一个最大的圆（内切圆），这个圆的面积是多少？

分析：如图2，如果我们按照常规的解题思路，要求圆的面积必须先求出圆的半径。在图中，圆的半径就是正方形边长的一半。因此，我们要想方设法求出正方形的边长。但是限于我们目前的知识，无法通过正方形的面积是60平方厘米而求出其边长的具体数值。为此，我们可以“声东击西”，将正方形平均分成4个小正方形，每一个小正方形的面积是15平方厘米。不难发现，小正方形的边长就是圆的半径，小正方形的面积也就是边长的平方，正好是圆半径的平方，即r2=15。所以，圆的面积πr2=15π平方厘米。一般情况下，要求圆的面积必须首先求出r，但在这里，我们偏偏不求r，而是求出r2，通过r2直接求出圆的面积。其中所展现的“声东击西”解题策略让人心服口服。

千变万化的数学习题犹如变幻莫测的战场。在小学数学教学中，运用“三十六计”巧解习题的例子还有很多，如“上屋抽梯” “金蝉脱壳” “反客为主” “调虎离山” “关门捉贼”等。这里，笔者仅举几个例子，并结合具体的数学问题做出简要的诠释，以期抛砖引玉，从中可以略窥数学的思想方法。