基于尺规作图培养学生的几何直观与推理能力

曹辰

摘 要：对于初中生而言，几何推理的学习存在一定的难度。利用几何直观，可以帮助学生把复杂的几何问题变得简明形象，有助于学生进行几何推理的学习。针对如何在课堂教学中培养学生的几何直观能力和推理能力进行了一些探索。通过尺规作图，引导学生运用“先直观，再推理”的分析方法，提高学生解决几何问题的能力。

关键词：几何直观能力；推理能力；尺规作图

一、研究背景

按照《义务教育数学课程标准（2011年版）》的规定，几何直观主要是指利用图形来分析问题。恰当地利用几何直观，可以帮助学生直观地理解数学，特别是抽象的数学内容；同时，借助几何直观还可以把复杂的数学问题变得简明形象，有助于提高学生解决问题的能力。在中学数学阶段，教师不仅要关注基础知识和基本技能的培养，也要关注学生高层次能力的培养。其中，培养学生的几何推理和几何直观能力是新课程标准的重要目标。

“尺规作图”一直是培养学生数学几何推理和几何直观能力的阵地之一。在初中数学教材中，与“尺规作图”相关的内容主要有：（1）作一条线段等于已知线段；（2）作一个角等于已知角；（3）作一个角的平分线；（4）作一条线段的垂直平分线；（5）过一点作已知直线的垂线；（6）利用三边、两边及其夹角、两角及其夹边作三角形；（7）已知底边及底边上的高线作等腰三角形；（8）已知一直角边和斜边作直角三角形。

在教师的实际教学中，几何直观和几何推理常常难以调和。前者注重直观形象，后者注重严密逻辑。在许多教师眼中，“尺规作图”常常被视为学生动手实践和操作的载体，而忽视作图中的几何推理部分。本文采用引导学生先通过尺规作图，直观感受几何图形的变化规律，再通过几何推理证明规律，最后在具体情境中应用规律的方式，对尺规作图在初中数学几何直观与推理能力培养上的应用进行了探索。

二、问题提出

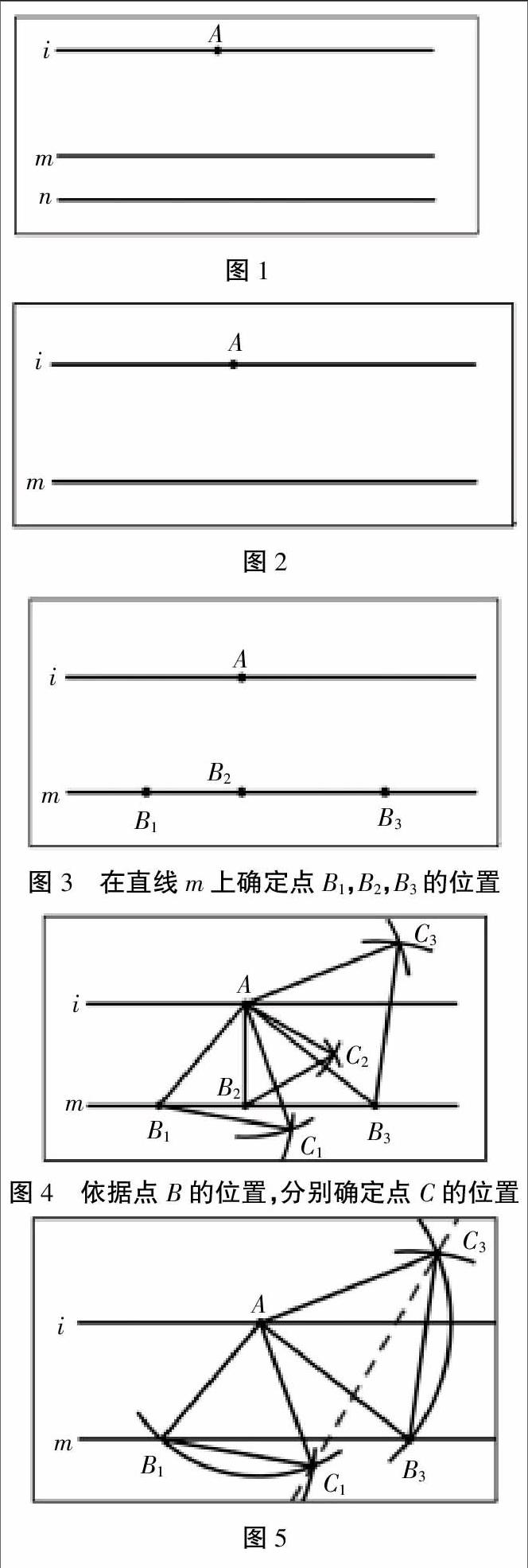
问题：如图1，平面上存在三条互相平行的直线m，n，i，点A为平面上的直线i上确定的一点。以A为顶点，利尺规作图画出等边△ABC，使得顶点B在直线m上，顶点C在直线n上。

在此题中，点A的位置已经确定。为了构造等边三角形，随着点B在直线m上运动，点C的位置也会随之改变。因此，直接确定点A，点B，点C分别在三条平行线上的具体位置会有很大的难度。那么，当点B在直线m上运动时，点C的运动规律是什么呢？为了更好地研究点C的运动情况，笔者将原有问题进行了改变。

三、问题转化

问题：如图2，平面上存在两条互相平行的直线i，m，点A为直线i上一点。点B在直线m上运动。以A、B为顶点，利用尺规作图画出等边△ABC。探究点C的运动规律。

在改变后的问题中，可以先在直线m上确定点B的位置，再通过作图去确定点C的位置。因此，需要在直线m上至少选取三个点B1，B2，B3（图3），各自完成等边三角形的作图，再根据点C1，C2，C3的位置（图4），通过几何直观去判断点C的运动规律。

在教学过程中，当笔者完成作图后，学生得到的初步判断是：根据几何直观，点C1，C2，C3的位置在同一条直线上。在通过推理对猜想进行证明，可以先将图4中的等边三角形△AB2C2忽略，将问题转化为两个等边三角形公共顶点的旋转问题，如图5。

图5中，在连接C1C3后，易证明△AB1B3≌△AC1C3与∠AB3B1=∠AC3C1，进而可以证明直线C1C3与直线m的夹角是60°。同理，若忽略等边三角形AB3C3的存在（图6），也可以证明直线C1C2与直线m的夹角是60°。因此，直线C1C3、直线C1C2与直线m的夹角都是60°，所以点C1，C2，C3共线。这个结论说明，当点B在直线m上运动时，点C的运动轨迹即为图5、6中的直线C1C3。

四、深层探究

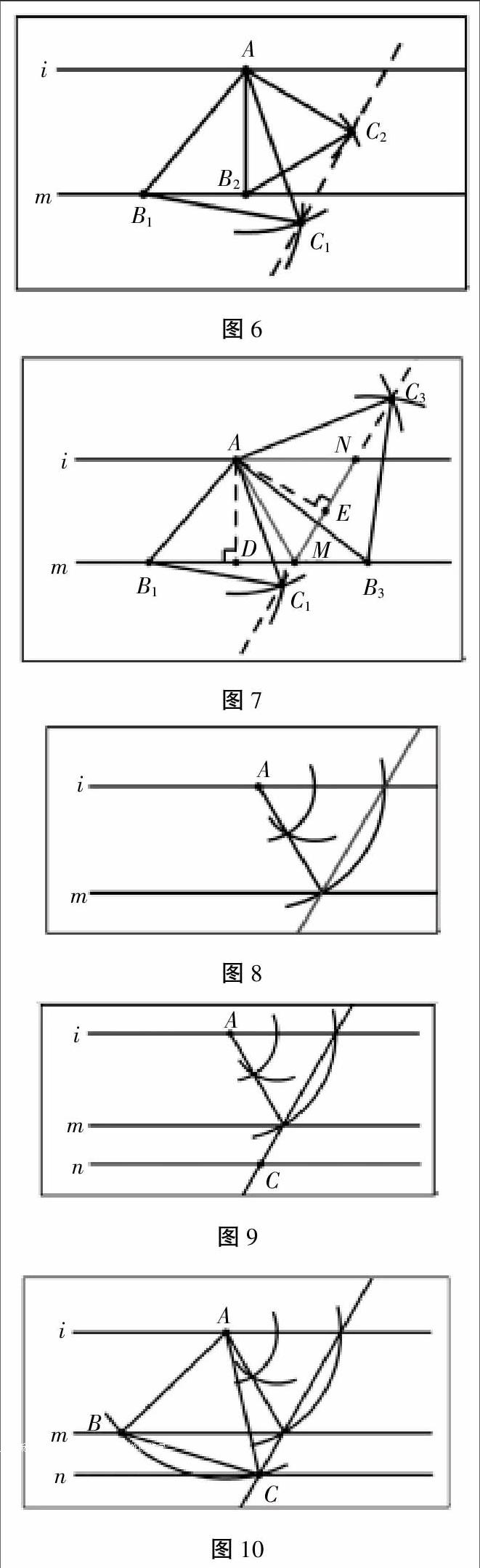
難道每次分析问题时都要画出两个等边三角形后才能确定点C的运动轨迹？能不能在确定点A的位置后，直接作出点C所在的直线？笔者带领学生在原来的基础上继续探究：

在图7中，设直线C1C3与直线m的交于点M，与直线i交于点N。作AD⊥直线m，AE⊥直线C1C3。在证明△AB1B3≌△AC1C3后，可得两个三角形的面积相等且底边B1B3=C1C3，因此垂线段AD=AE。

在图7中连接线段AM，根据角平分线逆定理，AM平分∠B1MC3；因此∠B1MC3=60°。再根据直线m∥i，可证明△AMN为等边三角形。

因此，在确定了点A的位置后，只要以点A为顶点，在平行直线m与直线i间构造等边△AMN即可。为了构造该等边三角形，需要先构造∠MAN=60°。作图过程如图8所示。图8中新出现的直线即为点C的运动轨迹。

最后，笔者带领学生重新审视最开始问题，根据上面的研究，可以根据点A与直线m的位置，直接作出点C的轨迹直线，如图9。再结合原题，可以得到如下结论：点C既会出现在直线n上，又会出现在轨迹直线上。因此，点C位于轨迹直线与直线n的交点上。

在确定了点C的位置后，线段AC即为等边三角形的边长。之后再利用圆规，以点A为圆心，AC长为半径画弧。其与直线m的交点即为点B的位置。顺次连接线段，即得到符合题目要求的等边△ABC，如图10。

五、研究反思

在几何教学过程中，教师往往对于几何直观缺乏应有的重视。教师习惯于关注推理的方法和结论，而对学生推理的思考过程有所忽视。对于一个完整的思考过程而言，往往是从对事物的初始认识开始的。尤其对初中生而言，正在经历从“算术”到“数学”，从具体到抽象的过渡。受学生逻辑思维能力的限制，很多学生在几何推理的学习上是有一定困难的。因此，在教师的几何教学过程中，借助于几何直观、几何解释，让学生通过“眼见为实”，帮助学生更好地理解和接受抽象的内容和方法，通过“图象语言，符号语言，数学语言”三结合的方式去学习几何，尤其是进行几何推理的学习。在探究教学过程中，可以让学生根据作图，先对结论进行直观判断，再对结论进行严格证明。这样的学习过程对于培养学生的几何直观能力和借助几何直观进行推理论证的能力有很大的促进作用。使用这种“先直观，后推理”的方式，我们可以解决很多类似的尺规作图问题。例如，在平面内任意三条直线上各取一个点，利用尺规作图使得这三个点为等边三角形、直角等腰三角形的顶点；或者在平面内的三个圆上各取一个点，尺规作图使得这三个点为等边三角形、等腰直角三角形的顶点。希望有兴趣的老师可以和笔者一起研究。

参考文献：

[1]秦德生，孔凡哲.关于几何直观的思考[J].中学数学教学参考，2005.

[2]刘晓玫.对“几何直观”及其培养的认识与分析[J].中国数学教育，2012.