组合公式的推广及应用

内蒙古呼和浩特土左旗金山学校 刘海军

组合公式的推广及应用

内蒙古呼和浩特土左旗金山学校 刘海军

文章对二项式定理，组合数公式进行了深入探讨，得出了一些新的性质、定理。通过对它们的恒等变形，在某些数列的求和方面进行了有效的应用，最后利用组合数学中的“查分表”法求部分和，此方法只需知道该数列的通项式，就可以求得前几项的和，而且格式固定，便于操作。

二项式定理；组合公式；查分表

一、应用二项式定理求某些组合数的数列求和问题

所谓二项式定理，是指设n是正整数，对于一切实数x和y，有

为了讨论方便，不妨把数列中的每项中的组合数之外的部分称为该项的系数。在中，令x=1，y=1得：

公式（1）（2）（3）是三个最基本的等式，许多组合数的数列求和问题，经过适当的变形整理后，都可以利用公式（1）（2）（3）得到有效解决。

1.系数成等差数列的数列求和问题

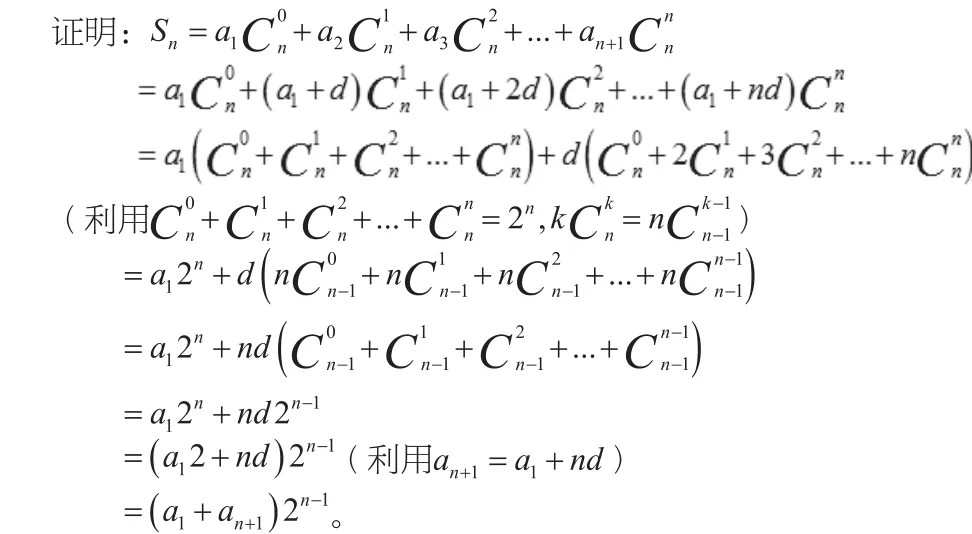
2.系数成等比数列的数列求和问题

解：由于a1=3a2=32a3=…3nan+1=3n+1，显然且{ai}（i=1,2，3…n+1）是以3为公比的等比数列。于是：

二、利用差分式求部分和

设任一数列h0,h1,h2,h3…hn… （9）

△h0,△h1,△h2,△h3…△hn…，

于是，数列（9）的差分序列是将每个k=0,1,2…阶差分序列列成一行而得到，如下所示：

若求形如h0,h1,h2,h3…hn的和。

定理3：设序列h0,h1,h2,h3…hn有一个差分表，该表的第0条对

总之，利用二项式定理、组合公式、差分表求和，其中二项式定理、组合公式及其变形定理在求和中表现得特别灵活巧妙。使原本抽象深奥复杂的运算，看似无法求和，但是能够通过巧妙运用这些定理及其变形得到很好的解决。而“差分表”求和的优点是格式固定，易于操作，但运算量较大，这就要求我们在学习中要善于总结，善于思考各种求和问题，要善于运用定理及其变形，使复杂问题简单化，使求和问题得到有效解决。