正确处理数学备课中的三大关系

张春明

摘 要 数学教师上课之前都要进行备课，而备课质量的优劣将直接影响到课堂教学的效果。所以，课前如何进行高质量的备课是高效教学的前提。根据数学这门课的特点，备课就是要处理好所授内容的学术形态与教学形态、预设与生成、差异性与整体性这三大关系。

关键词 备课 学术形态 教学形态 预设 生成

因为备课质量的高低直接影响到课堂教学的效率与学生吸收知识的效果，故教师要思考从哪些角度切入才能备出好课。其实人教社的章建跃博士早就给出了思路，他认为要“理解数学、理解学生、理解教学”[1]，笔者概括为“备教材、备学情、备评价”。本文探讨实际备课时要处理好的三大关系。

一、学术形态与教学形态的关系

现在的数学教材中呈现的内容并不是以该知识刚被发现时的原始面貌来编写的，而是经过若干年后的发生、发展和完善，编者以最严密、最简洁和最漂亮的形式呈现出来，所以教材中的内容已是高度的形式化和符号化，具有很强的抽象性，这便是教师要在课堂上传授给学生的数学知识，这种形式被称为数学内容的“学术形态”。如果教师照本宣科，按教材这样的编写形式来直接传授，学生会感到枯燥乏味，同时也给学生一种错觉：以为数学知识都是这样，与生俱来就很完美，数学家最初发现该知识时就很完整、很严密。然而历史事实并非如此，因为任何一个数学知识的产生和发展都不是一帆风顺的，期间都经历了一代代数学家们几十年、几百年甚至上千年的传承、创新或争论，才逐渐慢慢地发展起来直至完善[2]，而教材把这些已完善的数学知识通过“整容”变成了“冷美人”。这就需要教师根据学生的情况对教材中的数学内容进行有意识地再创造。比如，可以用现实生活中的实际例子来替代令学生感到陌生的教材中的引入；可以采用数学史上促使该知识产生的原始问题来探究；可以把当年数学家们对该知识点的争论呈现给学生辨析；可以把教材中比较抽象的数学语言转化为通俗的易于理解的语言传授给学生；等等。而所有这些教师在备课时的再创造，就是数学知识的“教学形态”。只有这样，学生才能体会到数学的趣味性，才会知道数学知识的产生绝非“冰冷的美丽”，也有“火热的思考”。

当然，在把教材中数学知识的“学术形态”通过备课转化为“教学形态”时，也不能随心所欲。比如，不能为了一味追求有趣而没有数学味，不能为了仅仅让课堂生动而使设计的例子失去科学性或没有思维含量，更不能脱离现实和数学本质而去刻意臆造情境。因此，教师在备课时始终要围绕所传授知识的数学本质，按照课标的要求抓住其核心内容，在此基础上进行再创造。既要能把学生学习数学的积极性充分调动起来，又能紧扣教材避免有“去数学化”倾向，而这都需要教师在备课时对教材进行二次开发。

案例1 函數的单调性概念

在高中数学苏教版必修1的2.2.1节“函数的单调性”中，该节课的教学目标就是要让学生理解函数单调性概念并能证明与求单调区间，因此教学重点显然就是函数单调性的概念，但教学难点是什么呢？仔细阅读教材，一开始就先给出一个气温变化图（如图1），然后写了一句话：怎样用数学语言刻画上述时间段内“随着时间的增加气温逐渐升高”这一特征？接着就直接给出增函数与减函数的概念，最后安排了两个例子：求单调区间与证明增函数。

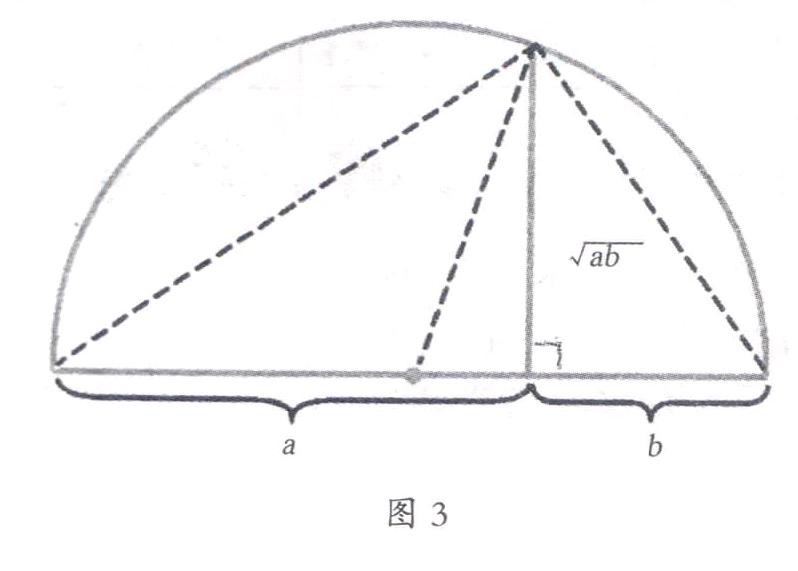
教材的编写就是典型的关于“函数单调性”这个知识的学术形态。以教材中单调增函数的概念为例：“一般地，设函数y=f（x）的定义域为I，区间I？哿A。如果对于区间I内的任意两个值x1，x2，当x1

显然，教材中的增函数概念非常精确也很严密，但抽象程度非常高，正是典型的高度符号化与抽象化的数学概念代表。这对于刚进入高中的高一学生来说，在理解上还存在难度。因“任意”涉及到了“无限向有限转化”的思想，这需要认知上的一个提升，属于质的飞跃，所以这个词的理解是本节课的教学难点。一旦学生突破了这个难点，理解了“任意”的含义，则表明学生从形象的感性认识上升到了抽象的理性认识，学会了如何从定量分析转化到定性分析，也进一步理解了高中数学概念中的形式化符号表征。

有了上述分析后就要思考：该怎样讲授才能突破这个难点呢？这只能从学生已有的认知基础出发才能循序渐进地理解。学生对函数的熟悉显然还只停留在初中所学的四个函数，包括它们的图象，所以一定要利用好这个前提而不能仅靠教材中给出的气温变化图这一个图象。另外要给学生一系列的问题去思考，怎样用数学语言来表达初中所讲的“增大而增大”这个描述。确定了这样一个教学思路和策略后，就可以对教材进行二次开发，设计出逐渐深入的问题串让学生去探究。

设计片断：首先展示图1，让学生直观感受日常生活中某一天出现的哪些时间段气温在升高或下降，然后针对“气温随着时间的增加慢慢上升”这个现象类比学生非常熟悉的函数f（x）=x2。学生根据图象自然会知道在[0，+∞]内f（x）是随x的增大而增大，接着就给出一个问题来探究：“怎样用数学语言来刻画f（x）=x2在[0，+∞]内f（x）是随x的增大而增大？”这就是要让学生学会用抽象的数学语言去表征形象化的文字语言。当然这样提问难度太大，学生也回答不了，故可分解成若干个小问题来降低难度，于是就设计了下列一些环环紧扣的问题串。

（1）当0<1时，有f（0）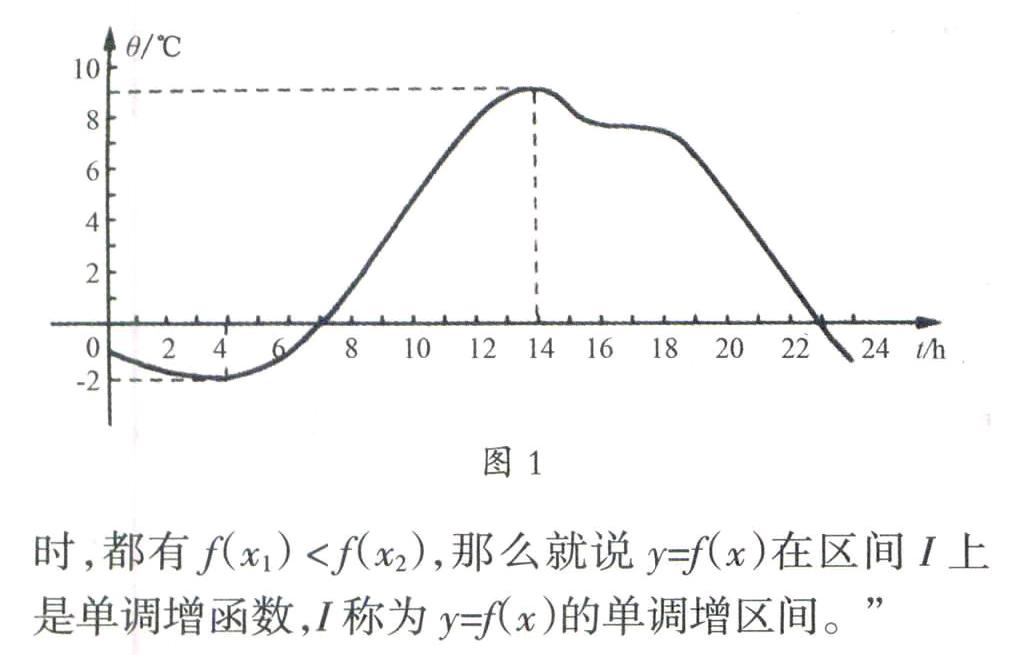

（2）当0<1<2<3<…时，有f（0）

（3）当有无数个x1

（4）如何才能让自变量x取遍区间里的所有值呢？难道真需要这樣一个接一个列举下去吗？

当学生探究思考到这儿，就会很自然想到要用字母来代替数字，此时概念的符号化表达就呼之欲出了，同时也把“任意”两字很轻松地解决了。教师还可以边问边用几何画板来演示f（x）=x2在[0，+∞]内点的运动轨迹，以增加教学的直观性。

上述设计片断便是教师授课时对单调增函数概念的“教学形态”，这样才能让学生易于理解抽象性的概念，即概念的“学术形态”，而刚才这个分析与思考过程就是备课中的一个环节。当然接下来的减函数概念理解也就水到渠成了。

二、预设与生成的关系

预设其实就是指对教学过程的预先设计，是对课堂动态系统的预先思考，通俗说法就是前面提到的“备课”过程。而生成是指教师在课堂的实际教学过程中产生的新问题，它可以是学生出乎意料的答案或想法，也可以是教师临时发现的有矛盾甚至有误的地方。

作为一名教师，对某一数学内容的教学过程进行预设后，在实际授课时可能会出现生成，而此时的生成经过教师反思后可成为下次传授此内容的预设，于是生成就转化为新的预设；同样道理，如果再在授课时又产生新的生成，则此次生成还可成为再下次更新的预设。预设、生成，再预设、再生成，如此继续循环下去，教师的预设就会越来越多，备课的质量也就会越来越高（如图2）。

案例2 基本不等式的证明

（3）结合恒等式变换来证明

教师准备好上述几种方法的预设还不够，因为这些方法都只是代数角度的方法，除此之外还要预设几何角度的证法。在苏教版教材上安排了基本不等式的几何意义（如图3），就是一个半圆模型。因此受此启发还有其他几何方法：构造圆模型、弦图模型等来推导[3]。即便预设了这么多的证法，仍然免不了课堂上可能还有其他意外证法的生成等。所以教师一定要不断积累课堂随时会产生的生成，并作为以后的预设，这样才能在遇到新的生成时不心慌，不被打乱节奏，并能顺利引导学生完成这节课的教学目标。

当然，预设毕竟是课前作的准备，是静态的，而课堂是随时在发生变化的一个动态过程。所以教师要因时因地，具体情况具体应变，既不要无视生成而一定要把预设全讲完，也不要因生成多了而抛弃事先的预设导致无法实现教学目标。由此可见，预设与生成这个矛盾统一体一定要处理得当。预设是前提，生成是过程，只要教师在备课时能充分考虑到“生成”的可能情况，就能在课堂上应对自如。

三、差异性与整体性的关系

心理学研究表明，人与人之间是有差异的。这些差异可以体现在记忆力、理解能力、动手操作实践能力等各方面。教师在课堂上授课时，虽然学生都在认真听讲，但他们的接受能力是不同的。这就要求教师在备课时需要考虑学生的个体差异性，还要考虑班级的整体性，也就是要保证每个学生都能达到这节课的教学目标。故在备课时，基于全体学生要掌握的基本教学目的，需要认真设计例习题，使它们的难度具有层次性，富有梯度。设计出符合不同程度学生的习题，既有让他们能独立完成的习题，又有各自“跳一跳够得着”的拓展题。

教师在提问、讲解时要从不同程度学生的最近发展区出发，巧妙灵活地应用各种教学策略或手段，围绕不同层次的学生设计出“恰时恰点”的问题。教师若能在备课时合理安排好差异性与整体性的关系，也就做到了“因材施教”和隐性的“分层教学”。

备课时还要考虑评价，即练习题和作业的配置，此时也要兼顾差异性与整体性。如安排一些整体学生须掌握的基础题与中等题，再安排一些拓展提高题，以训练思维的深刻性与发散性。因此无论课前、课中还是课后，都要认真处理好差异性与整体性的关系。

参考文献

[1] 章建跃.中学数学课改的十个论题[J].中学数学教学参考：高中版，2010（3）.

[2] 汪晓勤、韩祥临.中学数学中的数学史[M].北京：科学出版社，2002.

[3] 沈金兴.“形神兼备”之均值不等式欣赏[J].中学数学教学参考：高中版，2015（9）.

【责任编辑 郭振玲】