往复压缩机活塞杆的自激频率特征提取的研究

李晓博，江志农，李 欣，车熠全，徐丰甜，张进杰

(1.北京化工大学诊断与自愈研究中心，北京 100029；2.北京市轨道交通工程技术研究中心，北京 100089；3.新疆油气公司采气一厂，新疆克拉玛依 834000)

往复压缩机活塞杆的自激频率特征提取的研究

李晓博1，江志农1，李 欣2，车熠全3，徐丰甜1，张进杰1

(1.北京化工大学诊断与自愈研究中心，北京 100029；2.北京市轨道交通工程技术研究中心，北京 100089；3.新疆油气公司采气一厂，新疆克拉玛依 834000)

对活塞杆实际部件进行模型简化，在弹性梁弯曲振动理论的基础上，推导出活塞杆自激振动频率的存在；然后通过试验获取往复压缩机的活塞杆沉降位移信号，对得到的信号进行小波降噪，滤除其中的噪声信号，获得活塞杆实际自激振动频率，最后和理论值相比较，验证了活塞杆自激振动频率的存在。为提取诊断活塞杆类故障的特征参数提供参考。

往复压缩机；活塞杆；自激振动频率；小波降噪

1 前言

往复式压缩机是石油化工等行业中十分重要的通用机械，一旦发生故障而不能及时发现排除，就会造成十分严重的经济损失。而据调查，活塞杆类故障是往复压缩机故障中最严重也是最常见的一种类型[1]。

国内已有许多往复压缩机故障诊断方法，研究人员对活塞杆断裂故障做了很多研究工作：马波等采用声发射技术对活塞杆断裂事故进行早期预警并且预测活塞杆寿命[2]；杨波等通过对压缩机的热力和动力特性、压缩机机组振动以及压缩机活塞杆断裂仿真模拟进行计算，为压缩机活塞杆断裂的监测与报警提供了可靠的理论依据[3]；刘彤等研制的裂纹深度自动测量系统通过对裂纹扩展深度的自动跟踪监测、数据分析及曲线生成来检测设备的表面裂纹状态，也可用于活塞杆断裂故障的诊断[4]；吴冬果等对活塞杆的材料化学成分、机械性能、金相组织及机械加工等方面分析活塞杆断裂原因，并提出了改进措施[5]。

本文将从理论和试验上推导活塞杆自激振动频率的存在，为提取诊断活塞杆类故障的特征参数提供参考。

2 活塞杆自激振动

自激振动是某些系统在输入和输出之间具有反馈特性，并有能源补充，从而引起的振动[6]。而摩擦往往会引起自激振动。活塞杆部件在实际运动过程中，由于活塞和十字头受到摩擦力的作用，所以可能会产生自激振动。

为了进一步理论推导和试验验证活塞杆部件自激振动的存在，需要先建立活塞杆部件的力学模型，在理论上推导出自激振动频率的存在。

实际活塞杆部件在计算时较为复杂，十字头在其运动方向的垂直方向上的位移很微弱；而质量主要集中在活塞上。所以，如图1所示，计算模型主要从以下5点对其进行简化[7]：

(1)将活塞杆A段连接简化为固定接触。

(2)将活塞简化成规则圆柱体，将活塞杆简化为等截面梁。

(3)将活塞与滑道的接触简化为点接触，即连接方式为简支；

(4)将活塞与滑道之间的摩擦系数视为恒定不变。

(5)忽略活塞的转动惯量。

图1 活塞杆部件力学模型

简化模型中具体参数为：活塞杆有效长度(A段至B段)L，材料密度ρ，弹性模量E，截面积S，截面惯性矩I，单位长度质量ρl=ρs，抗弯刚度EI，活塞半径r，活塞质量m，转动惯量J，摩擦系数μ。

2.1 模型方程

活塞杆自由弯曲振动方程：

(1)

这是一个四阶常系数线性齐次偏微分方程，可以用分离变量方法求解。设梁具有如下形式的横向固有振动[8]。

y(x,t)=φ(x)q(t)

(2)

将式(2)代入方程(1)得：

(3)

其中φ(4)(x)表示φ(x)对x的4阶导数，式(3)还可以表示为：

(4)

可以看出，该方程右端均为关于x的函数，左端均为关于t的函数，并且x与t彼此独立，所以方程两端必同时等于一个常数。可以证明该常数非负，记其为w2≥0。因此，式(2)分离为2个独立的常微分方程：

(5)

其中

(6)

2.2 边界条件

在考虑该模型边界条件时，需要考虑活塞杆无摩擦振动和有摩擦振动2种情况。

(1)不考虑活塞杆的摩擦运动时，在简化模型中，其方程边界条件如下：

(7)

B端为简支端，所以B端处的挠度y为零，弯矩为零，即：

(8)

解频率方程tanβl-thβl=0，得到βil的特征根为：

i=1,2…

(9)

因此自由振动频率为：

wi=(βi)2(EI/ρl)1/2

(10)

(2)考虑活塞杆的摩擦运动时，其方程边界条件如下：

B端为无附加转动惯量的简支端，所以B端处挠度y和总弯矩均等于零，假设摩擦力指向A段为正，反之为负即：

(11)

在此边界条件下求解方程，需要先计算只在摩擦力作用下活塞杆部件的静态平衡位置函数y0(x)。

活塞杆简化模型受力如图2所示，活塞杆A端和B端分别受到剪切力FA和FB。同时分别受到弯矩MA和由于活塞产生的弯矩MB。其中，MB=±mgμr。因此，平衡方程如下所示：

(12)

图2 活塞杆简化模型受力示意

对任意x(除B端外)，解得在x点处的横截面剪切力FS和弯矩M为：

(13)

(14)

考虑边界条件：

(15)

式(15)代入式(14)计算得到:

(16)

最后得到只在摩擦力作用下，活塞杆部件的静态平衡位置函数为：

(17)

由于活塞杆无摩擦力自由振动时，其平衡位置为x轴。假设活塞杆无摩擦运动时的自由振动方程解为y(x,t)，可以证明，有摩擦运动时活塞杆的自由振动方程解为Y(x,t)=y(x,t)∓y0，验证如下：

将Y(x,t)=y(x,t)∓y0代入活塞杆弯曲振动方程(1)中，满足条件；代入边界条件方程(7)以及边界条件方程(11)中，满足条件。

通过上述论证可知，活塞杆在无摩擦和有摩擦振动时，自激振动频率相同，只是平衡位置不同。活塞杆无摩擦振动时平衡位置为x轴，而在有摩擦运动时平衡位置函数为∓y0。

因此，可以从理论上证明活塞杆自激振动频率的存在。

3 活塞杆自激频率试验验证

上述通过建立简化模型，根据弯曲振动方程和边界条件求得活塞杆自激振动频率，从理论上证明了活塞杆自激振动频率的存在。接下来，需要进行试验验证，通过分析位移传感器采集的活塞杆沉降位移信号，验证活塞杆自激振动频率的存在。

为了捕捉活塞杆振动幅值，通过安装在往复压缩机上的活塞杆沉降位移传感器采集活塞杆沉降位移信号，图3为活塞杆沉降位移传感器的布置，图4为一个周期的活塞杆沉降位移信号，并对该信号作离散傅里叶变换，图5为变换后的频谱。

图3 活塞杆沉降位移传感器布置示意

图4 一个周期的活塞杆沉降位移信号

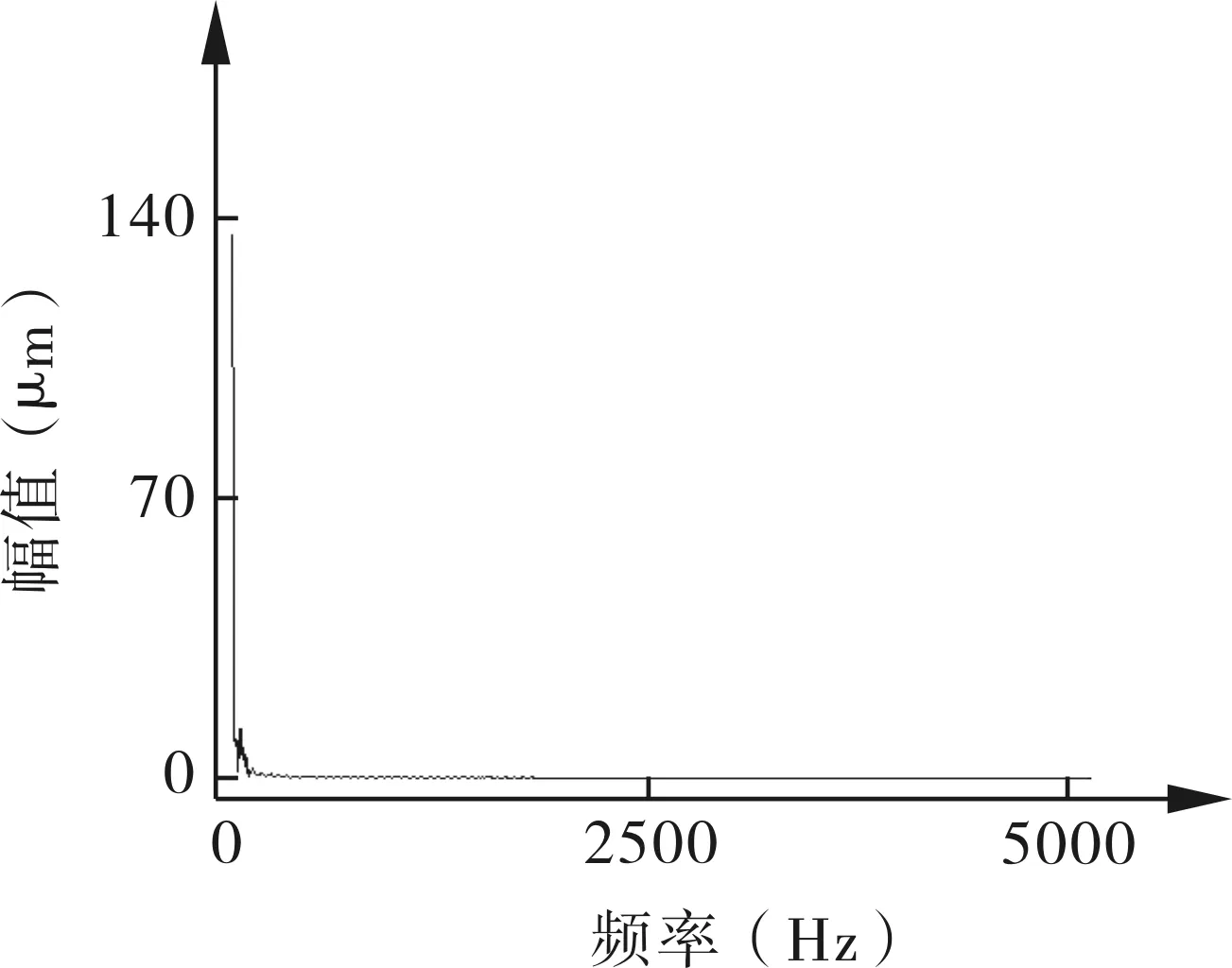
图5 变换后的频谱

由上文推导可知，活塞杆的振动频率处于高频部分。在该频谱图中，低频部分有较高的幅值，这可能是由于气缸内壁、活塞杆表面形位误差导致的，从而掩盖了其他频率范围的幅值信息。

小波变换，又称为小波分析，它是一种新的时域变换分析方法。它具有在时域和频域可以同时进行局部化的特点，它的多分辨率信号分析使得人们将它誉为“数学显微镜”。现在小波变换理论已经被广泛应用到了各种领域。

本文用小波降噪滤去低频干扰成分。图6，7分别是小波降噪之后的活塞杆沉降位移信号以及频谱图。从该频谱图中可见，低频范围的幅值基本为零，而其他频率范围的幅值得到显现。

图6 小波降噪之后的活塞杆沉降位移信号

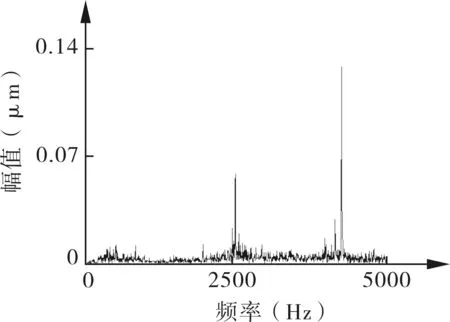
图7 小波降噪后的频谱

从图还可见，该信号经过小波降噪后，在w1=2560 Hz和w2=4340 Hz处幅值比较突出。由此可知,试验所得活塞杆自激振动频率分别为w1=2560 Hz和w2=4340 Hz。

试验用往复压缩机活塞杆部件的机械参数和活塞杆材料参数如表1所示。

表1 试验用活塞杆部件的机械和材料参数

在简化模型中，活塞杆截面为规则圆形，所以活塞杆截面惯性矩为[9]：

I=πD4/32

式中D——圆截面的直径

将表1中参数代入活塞杆自激振动频率方程得到如表2所示的特征解。

表2 活塞杆自激振动频率方程特征解

对比实际活塞杆沉降位移信号可知，当i=7和i=9时为方程的解。此时，w7=2643 Hz，w9=4302 Hz。误差分别为：

通过比较试验值和理论值，误差均小于5%，分析这可能是由于模型简化引起的偏差，因此可以验证活塞杆自激振动频率的存在。

4 结语

本文对活塞杆实际部件进行模型简化，在弹性梁弯曲振动理论的基础上，推导出活塞杆自激振动频率的存在；同时通过对往复压缩机活塞杆沉降位移信号进行小波降噪，滤除信号中噪声信号。最后通过试验验证了活塞杆自激振动频率的存在。说明在往复压缩机工作过程中活塞杆一直以特定频率在发生振动。这可以为提取诊断活塞杆类故障的特征参数提供参考。

[1] 陈鹏霏,贺宇新,关英俊.往复压缩机活塞杆疲劳强度校核理论研究[J].压缩机技术,2013(5)：1-5.

[2] 马波,高金吉,江志农.往复压缩机活塞杆断裂早期预警技术的研究[J].机械强度,2008,30(3)： 445-449.

[3] 杨波,倪继军,吕碧超，等.往复式压缩机组活塞杆断裂监测及联锁系统研究[J].流体机械,2003,31(6)： 30-32.

[4] 刘彤,杨荣根,张晓慧，等.疲劳裂纹深度自动监测系统的研制与应用[C].第十二届全国疲劳与断裂学术会议，2004： 288-290.

[5] 吴冬果,闫永兵,宋文戈.压缩机活塞杆断裂分析及技术改造[J].化工机械,2014,41(5)：690-692.

[6] 于德介,程军圣,杨宇.机械振动学[M].长沙：湖南大学出版社，2010.

[7] 徐丰甜.基于敏感特征参数的往复压缩机故障诊断方法研究[D].北京：北京化工大学，2015.

[8] 胡海岩.机械振动基础[M].北京：北京航空航天大学出版社，2005.

[9] 刘鸿文.材料力学[M].北京：高等教育出版社,2011.

Research on Extracting the Self-excited Vibration Frequency of the Piston Rod of the Reciprocating Compressor

LI Xiao-bo1,JIANG Zhi-nong1,LI Xin2,CHE Yi-quan3,XU Feng-tian1,ZHANG Jin-jie1

(1.Diagnosis and Self-Recovery Engineering Research Center,Beijing University of Chemical Technology,Beijing 100029,China；2.Safety detection and Intelligent System R&D of Beijing Rail Transit Engineering Research Center,Beijing 100089,China；3.The 1st Oil Production Plant of Xinjiang Oilfield of PetroChina,Kelamayi,834000)

A simplified model of the piston rod will be built.According to elastic beam bending vibration theory,the existence of the self-excited vibration frequency of the piston rod is deduced.Then to get the piston rod displacement signal by experiment.Meanwhile,the signal is de-noised with wavelet,and the real self-excited vibration frequency will be extracted from the de-noised signal.At last,comparing the theoretical value and real value to verify the existence of the self-excited vibration frequency of the piston rod.And this can provide reference for extracting the characteristic parameters used to diagnose the fault of the piston rod.

reciprocating compressor;piston rod;self-excited vibration frequency;wavelet de-noising

1005-0329(2017)01-0026-04

2016-04-18

2016-07-01

国家863计划项目(2014AA041806)；国家973计划项目(2012CB026000)；中央高校基本科研业务费专项资金资助项目(ZY1617)；北京市科委地铁机电设备故障监测与智能诊断系统研制及示范应用项目(Z131100004113004)

TH45

A

10.3969/j.issn.1005-0329.2017.01.005