不同叶片包角对螺旋形单蜗壳离心泵叶轮径向力特性的影响

张 霞，袁寿其，张金凤，黄 茜

(江苏大学国家水泵及系统工程技术研究中心，江苏镇江 212013)

不同叶片包角对螺旋形单蜗壳离心泵叶轮径向力特性的影响

张 霞，袁寿其，张金凤，黄 茜

(江苏大学国家水泵及系统工程技术研究中心，江苏镇江 212013)

为研究叶片包角对螺旋形单蜗壳单级单吸离心泵叶轮径向力特性的影响，应用CFD软件对某模型泵内部流场进行了数值计算，在保证蜗壳和其他叶轮几何参数不变的前提下，设计了3种叶片包角分别为110°、120°、130°的叶轮，模拟得到不同工况下叶轮所受径向力分布特性，并用外特性试验验证了数值模拟的可靠性。结果表明：设计工况下，作用在叶轮上的径向力最小，0.4Q下的径向力最大，且脉动幅值最大；叶片包角对叶轮所受径向力影响较大，以在额定工况下运行为例，叶片包角取130°时，径向力脉动最为紊乱，叶片包角取110°时，径向力脉动幅值较大；整体来看，叶片包角120°的方案性能最优。该研究可为低振动离心泵的水力优化设计、增强泵的运行稳定性提供参考。

离心泵；叶片包角；径向力；数值计算

1 前言

泵作为重要的能量转换设备及流体输送装置广泛应用于国民经济各个领域，其中70%使用到离心泵[1]。由于离心泵内部流动结构复杂，运行过程中，也常会出现一些问题，比如从泵启动到打开出口阀门，密封环常发生抱轴现象；叶轮口环和泵体口环粘接，必须要增加口环间隙才能正常启动，而加大口环间隙的同时就会带来容积损失，降低水力效率，严重影响经济运行[2，3]。有研究表明，发生上述问题的主要原因是螺旋形单蜗壳离心泵在偏离设计工况下运行时，产生的径向力过大，径向力的存在使得泵轴承受着一个交变应力，从而会造成泵轴的振动，增加泵的运行不稳定性[1]，所以对螺旋离心泵径向力的研究有很重要的现实意义。

目前许多学者采用试验方法和数值模拟方法对离心泵压力脉动和径向力进行了研究[4～6]，研究往往只着眼于通过考虑改变叶轮与蜗壳的间隙[7]、改变蜗壳隔舌型式[8，9]、改变蜗壳进口宽度[10]、添加分流叶片[11，12]，改变叶轮外径[13]等因素，而考虑通过改变叶片包角研究对径向力影响的文章较少。叶片包角是水力设计的关键几何参数，对离心泵性能有一定的影响[14～16]，外特性是内特性的具体表现，为进一步完善离心泵径向力分布特性的研究方法，有必要对叶片包角对离心泵径向力特性影响展开研究。

为此，本文在保证蜗壳和叶轮其他几何参数不变的前提下，设计叶片包角分别为110°、120°、130°的模型泵，通过外特性试验验证数值模拟的准确性，尝试对叶轮转动部件所受非稳态径向力进行计算，研究叶片包角对离心泵径向力特性的影响。

2 数值计算模型及方法

2.1 计算模型

研究对象为某一高比转数农业灌排用单级单吸离心泵，其主要设计参数如表1所示。

表1 模型泵主要设计参数

采用Creo软件对泵进行三维造型，在泵的其他几何结构参数不变的情况下，泵段模型(进口管道、蜗壳、出口管道)完全相同，建立了不同包角的叶片模型，叶片包角φ分别为110°、120°、130°，为了便于网格的划分，叶轮与蜗壳间隙部分的水体加在蜗壳上，为使流动能够充分发展，减少进出口边界位置对泵内部流动的影响，对模型泵进出口管路进行适当延伸，以提高计算的准确性[17]。本文的目的在于研究不同叶片包角对径向力特性的影响，采用非全流场进行数值模拟，以叶片包角120°为例，计算域如图1(a)所示。

(a) 计算域

(b) 结构化网格

图1 离心泵计算域与结构化网格

2.2 数值模拟

为了提高计算精度和效率，采用ICEM对计算域进行高质量的六面体结构网格划分，并对边界层进行加密。随即进行了网格无关性分析，以叶片包角为120°的方案为例，网格无关性结果如表2所示，由表2可知，随着网格数的增加，计算结果变化较小，趋于稳定，综合考虑到工作站的配置和计算时间，最终确定选用第3套网格方案，总网格数为3569692，其中进口管道网格数为333909，蜗壳网格数为1722388，叶轮网格数为1513395，网格划分如图1(b)所示。

表2 网格无关性分析

应用ANSYS CFX 14.5软件进行非定常数值模拟。采用SST k-ω湍流模型封闭雷诺时均方程进行求解，该模型同时具有k-ω模型计算近壁区域粘性流动的可靠性和k-ε模型计算远场自由流动的精确性。采用有限体积法进行离散求解，对所有变量进行整场联立求解，同时求解连续方程和动量方程组。

边界条件设置为总压力进口1.01×105Pa，参考压力为0 Pa，出口采用质量流量边界条件，计算域壁面采用无滑移网格函数，在定常计算中，动静域交接面采用Frozen rotor，采用高阶求解精度，收敛残差RMS设置为10-5，计算迭代步数最大800；在非定常计算中，以定常结果作为初始值，边界条件不变，而动静域交接面改成Transient frozen rotor，叶轮旋转8圈，且3°为1个时间步长，即3.44828×10-4s，总计算时间为0.3320349 s，并选取结果较为稳定的，第8个周期的结果作为分析。

3 计算结果及分析

为了分析泵内径向力特性，定义无量纲系数径向力K，其定义式为[18～23]：

式中F——径向力，Nρ——密度，kg/m3，取ρ=1000 kg/m3u2——叶轮出口圆周速度，m/sD2——叶轮出口直径，mmb2——叶轮出口宽度，mm

3.1 不同工况下径向力特性分析

3种方案的非定常计算均在多工况下进行，选取0.4Q、1.0Q、1.4Q3个典型工况，以叶片包角120°的方案为例进行分析，图2(a)为不同工况下作用在叶片包角120°叶轮上的径向力矢量分布。图2(a)中，各点的矢量坐标表达了某一时刻径向力的大小与方向。可以看出，当叶轮旋转一周，不同工况作用在叶轮的径向力时刻在变化，且呈规则分布，并与叶片数有关。这说明，叶轮所受径向力与叶轮和蜗壳之间的动静干涉作用相关，当叶轮扫过隔舌时，动静干涉作用增强，对叶轮产生的径向力从而随之增强。在额定工况下，径向力最小，但其值并不为0，这与理论值有所偏差，这是由于泵体的结构不对称导致液体在叶轮周围压水室中的速度和压力是非均匀，非轴对称而引起的。与小流量相比，大流量的径向力矢量分布图明显不同，这是由于小流量运行时，压水室中流速小，压力大；大流量运行时，压水室中流速大，压力小；小流量下撞击损失较大，对叶轮的径向力表现也更为突出。由图2(b)可以观察到：小流量工况下的径向力最大，振幅最大，说明此时受动静干涉作用最为强烈，在一个周期内，径向力脉动出现5个波峰和5个波谷。此外，可以发现与额定工况相比，大流量下的径向力脉动幅值依然很大，理论上而言，在额定工况下，液体在叶轮周围压水室中的速度和压力是均匀的，轴对称的，故理论上叶轮上的径向力近乎为零，而当运行工况偏大流量时，压水室中的液体流动速度不断增加，压力从隔舌处不断减少，所以大流量运行时对叶轮的径向力不会像额定工况下那么小，径向力脉动幅值于是依然大于额定工况下的脉动幅值。

(a) 径向力矢量分布

(b) 径向力时域

图3为不同工况下作用在φ=120°叶轮上的径向力频域特性，是由前文所定义的无量纲径向力系数K减去一个周期内平均无量纲系数做傅里叶变换得到的。由图3可以看出：3个工况作用下，径向力脉动主频在119.83 Hz，次主频在239.66 Hz，本文所研究模型泵转速为1450 r/min，叶片数为5，叶频为120.83 Hz，2倍叶频为241.66 Hz，由此可知，径向力脉动均以叶片通过频率为主。此外，在小流量工况下，作用在叶片上的径向力显然更易产生波动，且振幅较大，约为设计工况下振幅的8倍，可见偏低工况下运行不稳定性极大的增强，长时间小流量运行将严重影响使用寿命。

图3 不同工况下作用在φ=120°叶轮上的径向力的频域特性

3.2 额定工况下叶片包角对径向力特性的影响

图4为额定工况下不同叶片包角的叶轮所承受的径向力分布特性。由图4(a)和图4(b)通过比较可以看出，额定工况下，叶片包角对径向力分布有显著影响，叶片包角过大时，叶轮所承受径向力显著增大，且波动更为紊乱。叶片包角取110°和120°时，其波形较为一致，径向力大小相当，与叶片包角130°的方案存在相位差。由图4(c)可以发现，叶片包角为110°时，径向力振幅最大，且高频振动明显，而叶片包角取130°时，在小于1倍叶频处也有明显较大振幅，说明此时内部流动更为复杂紊乱。综合比较从径向力的角度不难发现，叶片包角取120°时，性能较优。

(a) 径向力矢量分布

(b) 径向力时域图

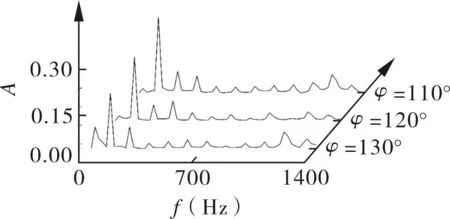
(c) 径向力频域图

图4 额定工况下不同叶片包角对叶轮径向力影响

图5为小流量工况0.4Q下，不同叶片包角的叶轮所受的径向力矢量分布。可以看出，小流量工况下，叶轮所受径向力分布周期性均很明显，周期与叶片数有关，大小约为额定工况下8倍，不同叶片包角的叶轮所受径向力分布各不相同，有明显相位差，但对其大小影响似乎很小，这可能是由于小流量工况下，叶片与隔舌之间的动静干涉作用增强，其作用超出了叶片包角对叶轮承受径向力的影响力。

图5 小流量工况下叶片包角对叶轮径向力

4 试验验证

按照径向力最优的选取原则委托某公司制造了1台叶片包角为120°的单级单吸离心泵，由于径向力试验需要在现场建立一套费用昂贵的测试装置，所以这里不考虑用径向力试验数据验证可靠性，仅从外特性的角度对模拟做可靠性验证。由于模拟得到的效率是水力效率而试验得到的是整机效率，两者不具备可比性，所以仅从扬程的角度分析数值模拟的准确性，数据对比如图6所示。在0.4Q～1.4Q范围内，数值计算的结果与试验结果有很高的一致性，尤其是在设计工况附近，最低误差可达2%，最高误差也仅有7%，究其原因，主要是模拟过程中没有考虑容积效率和机械效率等因素，但其误差在可接受范围内，表明本研究中用到的模拟方法是正确可信的。

图6 泵外特性测试数据与模拟数据对比

5 结论

(1)当叶轮旋转一周时，不同工况运行条件下，作用在叶轮上的径向力分布均比较规则，且设计工况下径向力最小，小流量工况下径向力最大。因此，螺旋形单蜗壳离心泵在小流量运行时，会存在一定的运行稳定性问题。

(2)叶轮所受径向力脉动频率与叶频有关，主频即1倍叶频处。在额定工况运行条件下，叶片包角增大时，径向力在低频振动明显，叶片包角减少时，径向力在高频振动显著。

(3)叶片包角存在最优值，使得离心泵在额定工况运行时，径向力脉动较小，总体来说，本研究中当叶片包角取120°时，性能最优。

(4)叶片包角对小流量运行条件下的叶轮所受径向力大小影响较小。这是由于小流量工况运行条件下，叶片与隔舌的动静干涉作用增强，其作用已超出了叶片包角的影响，从径向力矢量分布图上只能看出其明显的周期性，且周期与叶片数有关。

[1] 关醒凡．现代泵理论与设计[M]．北京：中国宇航出版社， 2011．

[2] 潘中永,陈士星,张大庆,等.叶轮口环间隙对离心泵性能影响的模拟和试验[J].流体机械,2013,41(11):10-14.

[3] 赵万勇.离心泵结构对大中型电动机窜轴的影响[J].排灌机械,2002,20(1):23-26.

[4] Guo S,Okamoto H.An experimental study on the fluid forces induced by rotor-stator interaction in a centrifugal pump[J].International Journal of Rotating Machinery,2003,9(2):135-144.

[5] Adkins D R,Brennen C E.Analyses of hydrodynamic radial forces on centrifugal pump impellers[J].Journal of Fluids Engineering,1988,110(1):20-28.

[6] Barrio R,Fernández J,Blanco E,et al.Estimation of radial load in centrifugal pumps using computational fluid dynamics[J].European Journal of Mechanics B Fluids,2011,30(3):316-324.

[7] 高波,王震,杨丽，等.不同口环间隙离心泵性能及水力激励特性分析及试验[J].农业工程学报,2016,32(7):79-85.

[8] Barrio R,Parrondo J,Blanco E.Numerical analysis of the unsteady flow in the near-tongue region in a volute-type centrifugal pump for different operating points[J].Computers & Fluids,2010,39(5):859-870.

[9] 施卫东,徐焰栋,李伟，等.蜗壳隔舌安放角对离心泵内部非定常流场的影响[J].农业机械学报,2013,44(S1):125-130.

[10] 江伟,李国君,张新盛，等.离心泵蜗壳进口边对叶轮径向力影响的数值模拟[J].水利学报,2014,45(2):248-252.

[11] 张金凤,叶丽婷,袁寿其，等.分流叶片对离心泵径向力特性的影响[J].农机化研究,2013,35(10):181-185.

[12] 袁寿其,周建佳,袁建平，等.分流叶片对螺旋离心泵径向力的影响[J].农业机械学报,2012,43(9):37-42.

[13] Gonzalez J,Parrondo J,Santolaria C,et al.Steady and unsteady radial forces for a centrifugal pump with impeller to tongue gap variation[J].Journal of Fluids Engineering,2006,128(3):454-462.

[14] 杨华,刘超,汤方平，等.不同叶片包角的离心泵试验与数值模拟[J].机械工程学报,2007,43(10):166-169.

[15] 王勇,刘厚林,袁寿其，等.不同叶片包角离心泵空化振动和噪声特性[J].排灌机械工程学报,2013,31(5):390-393.

[16] 曹卫东,李跃,张晓娣.低比转速污水泵叶片包角对水力性能的影响[J].排灌机械工程学报,2009,27(6):362-366.

[17] Worster R C.The flow in volutes and its effect on centrifugal pump performance[J].Proceedings of the Institution of Mechanical Engineers,1963,177(1):843-875.

[18] 周林玉.偏离工况下离心泵的压力脉动和振动分析[J].流体机械，2015，43(2)：52-55.

[19] 黄思，张雪娇，宿向辉.基于离心泵全流场的流固耦合分析[J].流体机械，2015，43(11)：38-42.

[21] 左章华.一种螺旋输送机的改进设计[J].包装与食品机械，2014，32(3)：63-66.

[22] 刘宏洋，何家波，顾新建，等.混凝土泵车的产品模块建模方法研究[J].机电工程，2014，31(8)：967-973.

[23] Zhang M,Tsukamoto H.Unsteady hydrodynamic forces due to rotor-stator interaction on a diffuser pump with identical number of vanes on the impeller and diffuser[J].Journal of Fluids Engineering,2005,127(4):743-751.

Effect of Different Blade Wrap Angle on Impeller Radial Force for a Helical Single Spiral Volute Centrifugal Pump

ZHANG Xia,YUAN Shou-qi,ZHANG Jin-feng,HUANG Xi

(National Research Center of Pumps,Jiangsu University,Zhenjiang 212013,China)

In order to investigate the effects of impeller wrap angle on the impeller radical force of the single-stage and single-suction centrifugal pump with single spiral volute ,the software CFD is applied to conduct the numerical calculation on the inner flow field of a model pump.Three kinds of impellers with different wrap angle are designed on the premise that the other geometric parameters of impellers and volutes are the same,and the wrap angle is designed as 110°,120° and 130°.Then,the distribution characteristics of radical force on the impeller under different conditions can be acquired through simulation.Besides,The reliability of numerical simulation is verified by the experiment of external characteristics.The results show that the radical force on the impeller is minimum under the designed condition and maximum under 0.4Q.Furthermore,the pulsating amplitude is also the biggest under 0.4Q.Therefore,the impeller wrap angle has a significant effect on the radical force.Taking the case under the designed condition for example,when the wrap angle is 130°,the fluctuation of radical force is maximum.When the wrap angle is 110°,the fluctuation of radical force is also big.On the whole,when the wrap angle is 120°,the performance of the scheme is optimal.This research can give reference for the hydraulic optimized design of centrifugal pump with low vibration and the improvement on operation stability of pumps.Key words: centrifugal pump;blade wrap angle;radical force;numerical simulation

1005-0329(2017)01-0043-05

2016-05-06

2016-06-17

国家自然科学基金资助项目(51009072)；江苏高校优势学科建设工程项目(PAPD)

TH311;S277.9

A

10.3969/j.issn.1005-0329.2017.01.008

张霞(1991-)，女，硕士研究生，主要从事流体机械内部流动特性的研究，通讯地址：212013 江苏镇江市江苏大学国家水泵及系统工程技术研究中心，E-mail:awedfcv@163.com。