跳出题海 整合变式题目—初三数学备考的策略研究
广东省佛山市南海区和顺第一初级中学(528241) 陈绮媚
跳出题海 整合变式题目—初三数学备考的策略研究
广东省佛山市南海区和顺第一初级中学(528241) 陈绮媚
一、问题的提出
每每经历完考试,老师们总会这样说,这道题目已评讲过,学生怎么还是做不出来?如此一来老师的责任已尽到,是学生没学好.我们深思这样的一个问题,为什么学生通过如此大量的训练,做过如此多相似甚至相同的题目,应试时仍然无所适从呢?
现在的初三数学教学中,“题海战术”仍然盛行,尤其是在第二轮复习中,教师要求学生做大量与中考题型一致的练习题,希望提高学生做题的自动化程度,从而提高解题的速度与技巧.题海战术作为应试教育的产物备受批评,但是一线的老师在实际中感觉题海战术是容易操作,并能见成效的.
笔者从题海中进行整合与变式,力求有所突破,尝试把题目进行“整合与变式”的学习法是否可以成为初三数学复习教学的可操作性的方法之一.
二、实验设计
(一)研究假设
本文作出以下假设: 题海战术与“题目的整合与变式”在提高初三学生的解题能力是没有区别的.
(二)概念的操作化定义和实验材料
1.题海战术
在本研究中,题海战术指学生通过做大量的与中考相同的练习题来训练数学的解题方法,练习内容为6册的数学书里面的经典题,难题以及中考模拟套题.学生利用一到两节课时间完成题目,老师利用相应的时间评讲,针对学生出错较多的题目讲解如何解题.
2.题目的整合与变式
对于知识点相同或者相似的题目,可以进行整合,对于元素较多的好题、难题,具有一定的延伸性的,可以进行变式训练.本研究主要集中在教材的内容进行讨论.
1)立足基础知识,回归课本,整合题目
六册课本中有大量的基础题,但是那么多的题目如何回归课本呢?笔者认为可以进行题目的整合.由于教材是按知识发展系统编排,根据学生的认知水平螺旋式上升,某个知识系统跨越了几个年级的学习.在学习知识的过程中,由于学生认识水平所限,无法把类似或者相同的内容进行横向整理,但在初三的复习阶段,学生对整个初中的内容已经有初步的整体把握能力.这时,要揭示相同或相似知识之间的联系需要进行整合,而不是流于形式的把书本的内容从头到尾在回顾一遍.所以为了使学生形成完善的认知结构,需要老师与学生一起把同一个知识体系的分散问题集中起来,同时加以归纳并系统化.
i.同一知识点的题目整合
这里以“两点间线段最短”这个知识点为例进行整合.
①(七年级)把弯曲的河道改成直的原理是___.
②(七年级上册113页4题)如图(1),在一个四边形各边上任意取一点,并顺次连接它们,想一想,你得到的图形周长与原四边形周长哪一个大?为什么?如果是一个五边形呢?六边形呢?
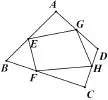
图1

图2
③(八年级下)证明: 三角形任意两边之和大于打第三边.
④(七年级上128页复习题10)如图2,在任意四边形ABCD内找一点O,使它到四边形四个顶点的距离之和最小,并说说你的理由.
设计意图: 题组训练,由浅入深,围绕着“两点间线段最短”的知识点层层推进.第①题根据题意直接写出公理,为后面的练习提供理论支撑,调动学生的知识结构.第②题直接运用公理.如果没有第①题的铺垫,学生虽然觉得本题简单,但是不知如何入手去回答题中的“为什么”.至于第③题是命题的证明,有一定的难度,需要严格的证明,只要用上公理,题目也迎刃而解.第④题是一道实际应用的提升题.
纵观这4道题目,第③④题学生不易解出题目,由于所需要的步骤不多,只需捉住最关键的公理即可.如果我们把这两道题目分散在备考的练习题中,学生不容易入手,捉不住解题关键,最后两题也无从下手.
这4道题目的整合,即回归了课本,逐层加深对“两点间线段最短”这个知识点的理解,明确这个考点的考查内容、形式,构建一个知识点的小体系,内化成自己的体系.
ii.同一解题性质、方法的题目整合
有些题目虽然不相同,但是在解题的方法上却异曲同工之妙.如运用对角线进行判定(特殊的)平行四边形这一类的题目,参数类型,数学思想方法等等.教师可以把解题方法相似的题目进行整合,更便于学生进行对照,从而掌握这一解题方法.这里以参数类型的整合为例
①已知关于x的方程3x+a=x-5的根是非负数,求实数a的取值范围.
②已知关于x的不等式2x-a≤1的解集为x≤-1,求a的值
上述两题的解题过程不尽相同,但是却用到同一种的方法,用参数把解(解集)表示出来.把这两道题目整合,在比较中掌握参数解题的方法,在对比中领悟两道题目的不同之处.
运用整合题目的做法,让学生通过题组进行反思,总结合适方法,从而通过题组训练可有效减少同类型题目的训练次数而达到“题海战术”的相同效果.
2)创新拔高,变式训练
中考的选拔性的考试,除了基础题以外,存在部分中难度题目,有梯度性地拉开考生间的距离,为了使学生应对这一部分题目,笔者认为对于课本中所遇到的难题,好题可以进行变式训练.
所谓数学变式训练,即是指在教学过程中对概念、性质、定理、公式,以及问题从不同角度、不同层次、不同情形、不同背景做出有效的变化,使其条件或结论的形式或内容发生变化,而本质特征却不变.也就是所谓“万变不离其宗”.数学教学改革专家顾泠沅创立的青浦四条经验中,其中一条“组织好课堂层次序列,进行变式教学”,强调变式训练在课堂教学中的地位.运用变式训练可以提高数学题目的有效利用率,提高教学实效,能更好地综合运用知识,有效培养学生综合思维能力,充分理解数学本质属性的作用.通过变式训练,是要防止形式地、机械地背诵、套用公式和定理提高学生变通思考问题和灵活应用概念、公式以及定理的能力.由于本文主要讨论的是初三复习策略,笔者下面讨论的是题目的变式.
i.寻找本质特征,一题多变
变式训练可以变换问题的条件和结论,变化问题的背景,但不变换问题的本质,使学生对问题的本质属性更全面的理解.通过变式训练使学生冲破事物的表象,引导学生注意到从本质看问题,全面地关注某一类题目的特征,注意从事物之间的联系的矛盾来理解事物的本质,在一定程度上可克服和减少思维的僵化及惰性.
从小学开始就有自主编题的练习,使学生能够根据已学的内容进行类比,创新题目.初中阶段,继续沿用这种题型,让学生自主编题.下面以初一的打折销售的应用题进行分析题目的变式.(参考《把学习的主动权还给学生》的教学案)
(北师大版七年级上册)例题1小明同学在一次调查活动中发现,一家商店将某种服装按成本价提高40%后标价,又以8折(即按标价的80%)优惠卖出,结果每件仍获利15元,这种服装每件的成本是多少元?
解: 设进价x元,得(1+40%)·x·80%=15+x把题目的整个过程以下面的流程图表呈现,寻找本质.

图3

图4
观察例题的图表,共有6个量?至少需要多少个量才能确定余下的量呢?
例题中是知道了三个箭头的信息(图4),但不知道三个价格,反过来,如果知道了三个表格能确定三个箭头的信息吗?又或者知道了一个价格与两个箭头的信息(图5),能确定余下的信息吗?知道两个价格与一个箭头的信息呢?(图6)

图5

图6
知道了六个量中的其中三个就能确定其余量.当然了,我们寻找到题目的本质属性时可以不断地变式.下面是其中的一道变式题.
自己尝试设计好打折销售问题的对应六个量,只留下三个已知量进行变式编题,如图7所示:
变式题目: 林伯伯以每颗树苗80元购进,培植一段时间后,提高一定价格售出,由于顾客购买量较多,以9折出售,最后林伯伯仍获利26.4%,问题: 李伯伯的提价率是都少?
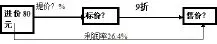
图7
打折销售的应用题所出现的量比较多,通过图表形式寻找个量间的联系,当理清各量间关系时,也就是找出了这一类题目的本质属性.仅做一次例题的练习对于大部分学生而言还没有找到这类题目的本质.但是从不断地变式中,学生能够逐步分析各量间的依存关系,也就是找到了本质.通过一题多变,学生从结构上理解具体情境的变式,体会情境的可变性与结构的不变性.
通过变式教学,不是解决一个问题,而是解决一类问题,遏制“题海战术”,开拓学生解题思路,培养学生的探索意识,实现“以少胜多”.
ii.培养发散思维,一题多解
一题多解的实质是以不同的论证方式,反映条件和结论的必然本质联系.在教学中老师要善于设置“一题多解”的变式训练,引导学生能从不同的角度,不同的知识,不同的思想方法解决同一个问题,使学生从单一的思维模式中解放出来,达到以创新方式来解答问题,培养学生思维的开阔性、发散性和灵活性.
(九年级下册)例题2如图,已知△ABC、△DCE、△FEG是3个全等的等腰三角形,底边BC、CE、 EG在同一直线上,且BC=1,连结BF分别交AC、DC、 DE于点P、Q、R.
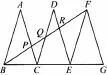
图8
(1)△BFG与△FEG相似吗?请说明理由;
(2)求AP∶PC.
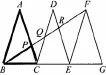
图9
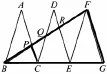
图10
分析: 对于第一问,通过题目所给的线段长度,可运用两边成比例且夹角两三角形相似.第二问可用两种方法解答,培养学生的发散思维.
方法一: 根据问题中的线段,选择证明△BCP与△ACB相似(图9所示),这对三角形的的位置是典型的交叉性,再根据相似寻找线段成比例,从而求出PC的长度,进而求两线段的比值.
方法二: 通过观察图形,存在好几对平行线,可找平行型的相似三角形(图10所示).根据二问中的线段以及三个全等的等腰三角形的条件,可证明△BPC与△BFG相似,可得根据合比性质得
本环节的两种解法,分别从两种构图方式上(图9、图10)证明两三角形相似,学生从复杂图形中抽取基本图形突破难点.一题多解,从题目条件出发,通过多个条件的不同整合,不同的方法却最终相同的结论,培养学生多角度,多方向地思考问题,有利于学生在应考中尝试不同路径去寻找解题方法,加快解题的速度.
iii.加强知识模块联系,一题多变
伽利略曾说过“科学是在不断改变思维角度的探索中前进的”.对于课堂数学教学要常新、善变,通过原题目延伸出更多具有相关性、相似性、相反性的新问题,深刻挖掘例习题的教育功能.
上述的几何例题2是一道综合性的好题,涉及到多个知识模块(相似的性质与判定,全等的性质,平行线分线段成比例,等腰三角形的性质)的综合运用.为了充分运用本题,使学生真正掌握本题的解题方法,下面的讨论中以例题2进行一题多变(一题多问、条件与结论互换、推广变式),加强多个知识模块的联系.
有效的数学基本功往往不是以单个概念(原理、法则)形式构成,而是以一种“模块”的形式存在于学生的数学认知结构之中的,这个的“模块”通过连结相关的基本概念、基本原理和法则所成,在具体的解决问题过程中,形成一些能够解决问题的、具有可操作性的技能、方法.
总之,在数学课堂教学中,遵循学生的认知特点,根据教材的内容,题目的特点加强变式训练,对巩固基础、培养思维、提高能力有着重要的作用.当然,课堂教学中的变式题很多都可以出自课本,体现出“源于课本,高于课本”,让学生也学会“变题”,使学生自己去探索、分析、综合,以提高学生的数学素质.
除此之外,在初三备考中还应该在学生的运算能力,审题能力等方面进行培养.如遇到难题时,我们可根据题目的条件猜想出题者的意图,所考察的知识点是什么等.
(三)被试
本研究的被试是我校的两个平行班,人数均为48人,两个班的班主任具有相近的资历,两个班风和学风接近,一个班是笔者任教的,另一个班的数学科任老师的教学成绩与笔者也相当.控制班进行“题海战术”,实验班进行题目的“整合与变式”.
(四)测量工具
实验的前测与后测材料分别采用《中考易》的三份模拟题,让学生进行了试验,每个题目标有项目的难度.部分题目进行修改,力求三份测试题难度相当.第二,三份模拟卷在实验的第8周,第12周进行.
三、试验的结果
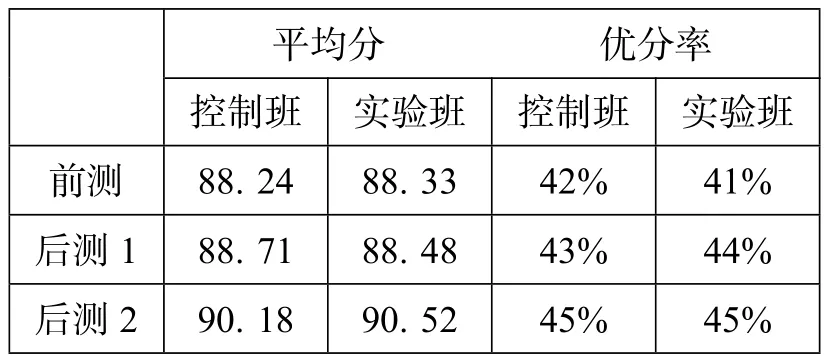
平均分 优分率控制班实验班控制班实验班前测88.2488.3342% 41%后测188.7188.4843% 44%后测290.1890.5245% 45%
从上述数据分析,控制班与实验班在本次教学试验中,题海战术与“整合与变式”的学习法对被试的水平影响没有显著差异,试验结果支持试验假设.两个班的平均分在两次后测中相差都在0.2分左右,非常接近.因此,两个班的成绩差异是极小的.
为了了解学生对题海战术和“整合与变式”的学习法的态度,笔者对两个班的部分被试进行访谈.控制班的受访被试反映: 对于平常的做题以及教师对一些偏难的题目进行讲解感觉比较乏味.做过的题目容易忘掉,不知道自己掌握了多少知识.
实验班的受访被试者对所采用的教学方法较为认同,认为自己在学习过程中感到比较踏实,能够知道自己每节课掌握了哪些基本知识,会做哪些难题.他们认为难题的障碍主要是自己不会类比已学过的题目,通过变式训练很好地积累了数学活动经验.
四、结论
做大量与中考题型相同的练习成为中考教学的主要手段之一.题海战术的目的是试图通过与考试内容和形式相同的训练,让学生做题过程自动化.多年来的备考中也证明,通过做大量与中考题型相同的模拟试题,是提高学生成绩的途径之一.
采用“整合与变式”的学习法,学生的输入量减少了,做中考的模拟试题也少了,但是学生的考试成绩并没有受到影响.试验结果显示,题海战术和“整合和与变式”的学习法在影响效果上没有区别,但“整合和与变式”的学习法更有利于学生的可持续发展.
五、局限性
本研究是在初三复习阶段,试验时间为12周,时间是否充足有待考证.研究的对象仅仅是本校的两个班,局限于某一地区的一所学校的个别班级的学生.因此,还需要进一步的研究,以便更加清晰地显示题海战术和“整合与变式”对考试的效应.
[1]梁惠燕.中小学教育科学研究的N个问题[M].广东高等教育出版社,2014: 212-220
[2]章飞.把学习的主动权还给学生[M].北京师范大学出版社,2013: 158-163
[3]马复.初中数学教学策略[M].北京师范大学出版社,2010: 305-308

