一道平面几何竞赛题的推广

广东省中山市教育教学研究室(528400) 方勇

一道平面几何竞赛题的推广

广东省中山市教育教学研究室(528400) 方勇

在李胜宏、陶平生教授等主编的《高中数学竞赛专题讲座》(浙江大学出版社出版,2007年6月第一版)系列教材平面几何分册中,有一道例题引起了笔者的兴趣:

第33页:例1过正△ABC外接圆的弧AC上一点P作PD⊥直线AB于D,作PE⊥直线AC于E,作PF⊥直线BC于F.求证:

图1

这道题看似简单,但它却融合了平面几何中的四点共圆判定及性质、西姆松定理和张角定理应用,设计十分精妙,是一道非常好的高中数学竞赛题.该书给出本题证明如下:

证明: 由PD⊥直线AB于D,作PE⊥直线AC于E,作PF⊥直线BC于F知A、E、P、D及E、F、C、P分别四点共圆,则∠DPE=∠BAE=60°,∠EPF=∠ECF=60°.由西姆松定理知,D、E、F三点共线,从而以P为视点,对△PDF应用张角定理,有

上述巧妙而又简洁的证明,引起了笔者的兴趣.注意到证明过程中,等边三角形三角的等量关系在最后的等式中约去,而四点共圆判定、西姆松定理及张角定理均在本题中对一般三角形都适用,这不禁引人思考: 若为一般三角形,本题结论是否成立或者结论应该如何?

经探索,笔者发现本题结论具有一般性,即对一般三角形本题结论推广如下:

△ABC的三边和三角分别为a,b,c及A,B,C,过△ABC外接圆的弧AC上一点P作PD⊥直线AB于D,作PE⊥直线AC于E,作PF⊥直线BC于F.则有:

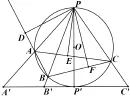
图2

证明如下: 过P作圆O直径交圆O于P′,过点P′作切线,延长PA,PB,PC分别交切线于A′,B′,C′.由∠PP′B+∠BPP′=90°,∠PB′P′+∠B′PP′=90°及圆周角定理,有 ∠PP′B= ∠PB′P′= ∠PCB故△PCB∽△PB′C′所以

推广后的结论更具一般性,证明看似比原题证明复杂,实际上却只运用了初中平面几何中常规基础知识,避免了使用西姆松定理、张角定理等较为精巧的知识,也许应证了数学中越一般知识来得越复杂的说法吧.

[1]李胜宏、陶平生等,高中数学竞赛专题讲座——平面几何[M],浙江: 浙江大学出版社,2007.