2017年高三文科数学高考模拟卷

广东汕头聿怀中学(515041) 黄毓君 郑妍 李佩芳

2017年高三文科数学高考模拟卷

广东汕头聿怀中学(515041) 黄毓君 郑妍 李佩芳

一、选择题(共12小题,每小题5分,共60分．在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案涂在答题卡相应的位置上)

5.一个几何体的三视图(从左往右: 正视图、侧视图、俯视图)如下,则该几何体的表面积是

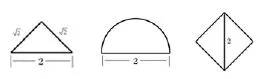
图1

7.已知α,β是两个不同的平面,m,n是两条不同的直线.给出下列命题:

①若a⊥b,a⊥c,b⊂α,c⊂α,则a⊥α;

②若α⊥β,α∩β=m,n⊂α,则n⊥β;

③若m⊥α,m⊂β,则α⊥β;

④若α//β,α∩γ=m,β∩γ=n,则m//n.

其中真命题的个数是

A． 0 B． 1 C． 2 D． 3

8.运行以下程序时,执行循环体输出的数据是

A. 0 B. 1 C.2 D.3

10.矩形ABCD中,AD=1,AB=2,现向矩形ABCD投一粒金子N(金子的大小忽略不计),则使得的概率是

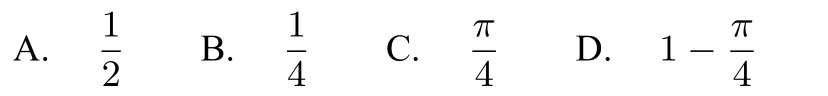
11.1 0.三棱锥P-ABC中,∠BAC=90°,M是BC中点,PM⊥面ABC,AB=AC=PM=2,则该三棱锥的外接球表面积是

A. 2π B. 4π C. 9π D. 10π

A. a＜b＜c B. a＜c＜b

C. b＜c＜a D. c＜b＜a

二、填空题(本大题共4小题,每小题5分,共20分,将正确答案填在答卷相应的位置上)

13.设抛物线x2=2y上一点P到x轴的距离是4,则点P到该抛物线焦点的距离是___．

16.整数列1,1,2,3,5,8,13,21,34,55,89···,这便是奇妙的斐波那契数列,它有一些美妙的特性,比如:

(1)任何相邻两个数,它们的位置越靠后,第一个数与第二个数的比值越逼近黄金分割0.618,称为黄金比率;

(2)从第2项起,任何相邻的三个数a,b,c,前两个数之和等于第三个数,即a+b=c;

(3)从第2项起,每个奇数项b与它的前后两项a和c满足关系式: ___.

三、解答题(6小题,共70分.解答应写出必要的文字说明,证明过程或演算步骤)

17.(本小题满分12分)为锻炼学生们的应用能力,数学老师把学生们带到学校操场,定位了学校操场上的东西方向上距离为40米的B、C两点,要求学生们利用工具做相关测量.一学生测得学校对面的小区楼顶A在B点的东偏北60°、仰角60°的方向上;楼顶A在点C的西偏北30°方向上.请你根据该生的测量结果:

(1)计算小区楼高AO;

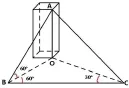
图2

(2)求∠ACB的余弦值.

18.(本小题满分12分)某校欲从甲、乙两名学生中推选一名学生参加“元宵灯谜比赛”.现有甲、乙两名同学过去8次参加灯谜比赛的成绩,成绩如下,但乙有一个成绩不小心丢失(每次比赛中每小题5分,满分150)

甲: 135,100,125,120,125,110,115,130

乙: 140,105,125,130,125,100,115

(1)以百位和十位为茎,个位为叶,在下图中作出以甲、乙两名学生比赛成绩的茎叶图,求出甲所有成绩的众数和中位数;

图3

(2)若乙丢失的成绩不小于110分,求甲的平均成绩超过乙的平均成绩的概率.

(3)若甲的平均成绩与乙的平均成绩相等,试分析该校该派哪一名学生参加比赛?说明为什么?

19.(本小题满分12分)已知斜四棱柱ABCD-A1B1C1D1的棱长均为2,点M为线段CC1的中点,AB⊥AD,∠DCC1=∠BCM = 60°,点 C1在面ABCD的投影Q∈CD.

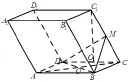
图4

(1)求证: 平面ACM⊥平面BDD1B1.

(2)求点O到平面ADM的距离.

(1)求椭圆C的方程.

(2)四边形OANB是以ON为直径的圆的内接四边形.设抛物线E的焦点为F,直线AF与抛物线交于另一点M,求抛物线E的方程及△AOM的面积.

21.(本小题满分12分)已知函数

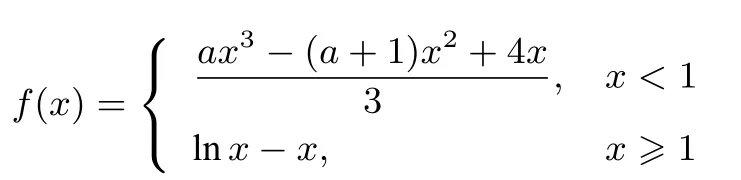
(1)求曲线y=f(x)在点x=2处的切线方程;

(2)讨论函数f(x)的单调区间

请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.

22.(本小题满分10分)选修4-4: 坐标系与参数方程

23.(本小题满分10分)选修4-5: 不等式选讲已知函数f(x)=|x-a|+|x-1|(a＞1)

(1)若对任意的x∈(-∞,1]时,f(x)+x2＞3恒成立,求实数a的取值范围;

(2)若不等式f(x)＞1的解集是{x|x＜1或x＞a},求实数a的值.

(答案略,如有需要请联系编辑部: mathyj@scnu.edu.cn)