无穷序列空间上紧性问题探讨*
赵文强, 张一进
(1.重庆工商大学 数学与统计学院,重庆 400067;2.重庆邮电大学 理学院,重庆 400065)
无穷序列空间上紧性问题探讨*
赵文强1, 张一进2
(1.重庆工商大学 数学与统计学院,重庆 400067;2.重庆邮电大学 理学院,重庆 400065)
紧性概念是泛函分析的重要内容,在现代分析学中应用广泛;考虑lp,p≥2空间上的集合紧性问题,证明了M⊂lp为预紧集的重要条件是M一致有界且一致收敛,并给出了一个应用实例.
无穷序列空间;预紧集;ε-网;一致收敛
无穷序列空间:
具有范数:
其中p>0,是一类重要的Banach空间,在各种泛函分析教程中被广泛应用.文献[1]讨论了特殊序列空间l2和c0上有界线性算子的矩阵表示.文献[2]研究了序列空间上的有界逼近和有界紧逼近性质.这里考虑一般情形lp(p>0)空间上集合的紧性问题,给出紧性的充要条件.
首先,给出紧集的相关定义和结果.
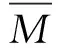
定义2 设X为度量空间,M⊂X为X的子集,N⊂M,ε>0.若对任意的x∈M,总存在y∈N,使得x∈U(y,ε),那么称N是M的一个ε网;如果N还是一个有限集合,则称N是M的一个有限ε网.
为了便于判断集合的紧性,在度量空间中有下面的等价命题[3-5].


引理2 设X为完备度量空间,M⊂X为X的子集,则M是X中的相对紧集的充要条件是对任意的ε>0,M在X中存在有限ε-网.
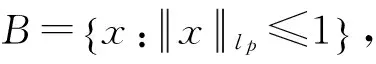
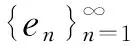
所以B不是紧的,同时也不是相对紧的.
定理1 设2≤p<∞,M为lp的子集,则M为预紧集的充要条件是:
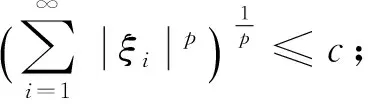
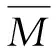
(1)
其中U(ξj,ε)为ξj的ε领域,j=1,2,…,s.令
(2)
于是,对任何的ξ=(ξ1,ξ2,…)∈M,根据式(1)知存在某个ξj,1≤j≤s,使得ξ∈U(ξj,ε),从而
(3)
故利用式(2)和式(3),及三角不等式立即得到:
因此,令ε=1就证明了条件(a).另一方面,对上述的有限ε-网{ξ1,ξ2,…,ξs},显然可以找到共同的i0=i(ε)>0,使得当i≥i0时,有
(4)
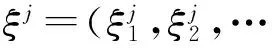
这表明对充分小的ε,有
(5)
于是,条件(b)得证.
充分性.对任意的ε>0,根据条件(b),存在i0=i(ε)>0,当i≥i0时,对任意的ξ=(ξ1,ξ2,…)∈M,有
(6)
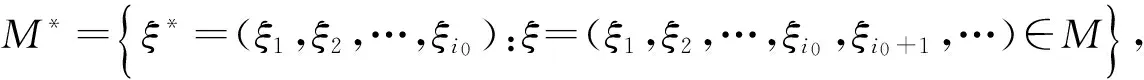
所以M*是Ri0中的有界集.于是,M*是Ri0中的预紧集.因此,由引理2知,存在有限个点ξ1*,ξ2*,…,ξs*∈M*,使得对任意的ξ*=(ξ1,ξ2,…,ξi0)∈M*,存在某个ξj*,j=1,2,…,s,使得
(7)
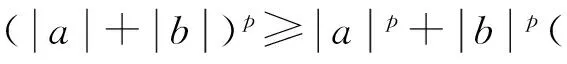
(8)
现在零延拓ξ1*,ξ2*,…,ξs*.即令
(9)
则这样得到的有限个无穷序列ξ1,ξ2,…,ξs属于lp.因此,根据式(5)和式(7),对任意的ξ=(ξ1,ξ2,…)∈M,有
即按式(8)定义的元素构成的集合{ξ1,ξ2,…,ξs}为M在lp中有限ε-网.再一次运用引理2,充分性得证. 证毕.
作为上述定理的应用,这里给出一个例子.
例1 取M为可数个无穷序列构成的集合.即M={Tn:n=1,2,…},其中
(10)
下面证明M满足定理1的条件(a)和(b).事实上,利用不等式当x>0时,ln (1+x)≤x,对于p≥2,可得:
(11)
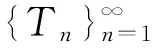
于是,当i≥i0时,对所有的n成立:
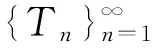
[1] 李嘉,李扬荣.关于序列空间上的有界线性算子的教学探讨[J].西南师范大学学报(自然科学版),2012,37(6):25-229
LI J,LI Y R.A Discussion on Bounded Linear Operators on Sequences Spaces[J].Journal of Southwest China Normal University(Natural Science Edition),2012,37(6):225-229
[2] 林贵华.序列空间中的逼近性质[J].大连理工大学学报(自然科学版),1996,36(1):1-5
LIN G H.Approximation Properties in Sequences Spaces[J].Journal of Dalian University of Technology(Natural Science Edition),1996,36(1):1-5
[3] 程其襄,张奠宙.实变函数与泛函分析基础[M].北京:高等教育出版社,2003
CHENG Q X,ZHANG D Z.Basis of Real Variable Function and Functional Analysis[M].Beijing:Higher Education Press,2003
[4] 郭懋正.实变函数与泛函分析[M].北京:北京大学出版社,2005
GUO M Z.Real Variable Function and Functional Analysis[M].Beijing:Peking University Press,2005
[5] 李国祯.实分析与泛函分析引论[M].北京:科学出版社,2004
LI G Z.An Introduction to Real Analysis and Functional Analysis[M].Beijing:Science Press,2004
责任编辑:李翠薇
Discussion on the Compactness in Space of Infinite Sequences
ZHAO Wen-qiang1, ZHANG Yi-jin2
(1. School of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067, China;2. School of Science, Chongqing University of Posts and Telecommunications, Chongqing 400065, China)
The notion of compactness, which is an important content in functional analysis, is widely used in modern analytical science. In this article, the compactness of set is discussed inlp,p≥2. It is proved thatM⊂lpis pre-compact set inlpif and only ifMis uniformly bounded and uniformly convergent. As an application, an example is presented here.
space of infinite sequences; pre-compact set;ε-net; uniform convergence
10.16055/j.issn.1672-058X.2017.0001.009
2016-04-16;
2016-05-20.
重庆市自然科学基金(CSTC2014JCYJA00035);重庆市教委科技项目(KJ1400430).
赵文强(1969-),男,四川南江人,博士,副教授,从事泛函分析及其应用研究.
O177.3
A
1672-058X(2017)01-0045-03

