基于DSP的焊装机器人控制算法研究与仿真设计*

邓 顺, 周康渠

(1.重庆理工大学 机械工程学院,重庆 400054；2.长安汽车智能制造技术研究所,重庆 401120)

基于DSP的焊装机器人控制算法研究与仿真设计*

邓 顺1,2, 周康渠1

(1.重庆理工大学 机械工程学院,重庆 400054；2.长安汽车智能制造技术研究所,重庆 401120)

在建立六自由度焊装机器人D-H坐标系及确定各手臂参数的基础上，研究其正逆运动学方程，设计其数值模拟算法，并在MATLAB环境下建立仿真模型，获得在定点控制模式下各个关节电机控制量，得到具有固定重力补偿的机器人控制模型；基于六自由度机器人动力学控制原理，在考虑电机特性及机器人手臂动力学特性的基础上，建立了具有传感器反馈控制的优化模型；在Tecnomatix环境下创建了四机器人焊接工位，利用其提供的Robotics功能模块，实现了机器人的路径及功能示教；利用DSP(Digital Single Processor，数字信号处理器)解算了机器人关节坐标的牛顿-欧拉逆运动学方程，并实时、快速处理传感器反馈信号，实现了对多个伺服系统的闭环控制。

机器人正逆动力学;数字信号处理器;实时控制

微电子科技及大规模集成电路在自动控制领域的广泛运用，对机器人控制模型的实时性能及控制精度都提出了严峻的挑战，例如在利用机器人磨削水轮机叶片时，对控制精度非常敏感，系统的控制精度直接影响叶片复杂型面的形位误差。然而，利用通用处理器解算控制模型时，控制的实时性以及对传感器反馈信号的处理都不满足要求。所以，设计能够实时处理机器人关节电机传感器信号的控制模型及其数值算法就成了研究热点。现代控制理论表明，在对一个复杂系统进行健壮控制的时候，建立精致的偏微分方程模型往往是困难重重的，所以，在简化的数学模型上建立有效的系统反馈，不仅能提高系统控制的可靠性，而且还能够减小模型误差内在的不确定性，从而设计出实用有效的控制算法。近年来，国内外学者为关节机器人控制模型做了大量的研究工作，并应用当前较为成熟的DSP(Digital Single Processor)技术对关节电机反馈信号实时处理，从而构建了许多强反馈的健壮控制模型。DRAKE研究了在TMS320C30 DSP芯片上实现六自由度球形手腕关节机器人运动学和逆动力学算法的可行性及实时性，并在统一的笛卡尔坐标系下实现了牛顿-欧拉逆运动学坐标变换[1]。KABUKA则在PD77230 DSP芯片上运用牛顿-欧拉逆运动学方程实现了对多个机器人手臂的控制，在这种并行任务中采用了主从机控制模式，减小了控制器总线开销，从而提高了控制速度和实时性[2]。二者在方法上都利用了数字信号处理器快速、实时的特点，并将其运用到计算机器人关节的运动学方程，起到了较好的效果，但是，这个计算过程中并没有处理编码器的反馈信号，即没有实行闭环反馈控制，稍显不足。在本文中，建立了焊接机器人实时控制的数学模型，并利用TMS320C2812 DSP芯片解算机器人的牛顿-欧拉逆运动学方程，并引入了交流伺服电机的反馈量，实现了对焊装机器人关节手臂的实时控制，并在Tecnomatix环境下完成了仿真验证。

1 建立模型

1.1 运动学模型

六自由度焊装机器人手臂的机构简图如图1所示，每个关节上安装一个交流伺服电机，通过减速器带动各个关节做旋转运动，连接传动轴的编码器实时反馈电机的角位移和转速。机器人的所有6个关节均为转动副，杆0至杆6连接各个关节，其轴线均在同一个平面上，并且关节4至关节6的轴线交于一点，这就构成了机器人逆运动学方程存在解析解的充分条件，故采用这种结构的机器人其前3个关节用以确定后3个关节的位置，而后3个关节确定了机器人的指向，通常也称后3个关节为机器人的腕关节[3]。当机器人的机械结构确定之后，用D-H(Danevit-Hartenberg)方法建立机器人各杆的传动轴坐标系，如图2所示，利用建立的坐标系得出D-H参数：杆件长度ai、杆件扭角αi、关节距离di、以及关节扭角θi，其中i=0，1，…，6，如表1所示。

图1 六自由度焊装机器人手臂机构简图Fig.1 Six DOF welding robot arm mechanism

图2 焊装机器人及其D-H坐标系Fig.2 Welding robot and its D-H coordinate system

杆号参数ai/mmαi/°di/mmθi/°1312900q12107500q230900q340-901280q450900q56001240q6

即

(1)

用D-H参数求解式(1)时，从系i-1到系i的变换矩阵i-1Ai可以表示为

(2)

其中si≜sinθi，ci≜cosθi，sαi≜sinαi，cαi≜cosαi，因为机器人的后3个关节用以确定腕的指向，故利用式(2)可以将系3到系6的齐次变换矩阵表示为如下形式：

3A6=3A44A55A6=

(3)

此时可以将控制量确定为q=[q1,…,q3,θ4,θ5,θ6]，然后由机器人前3个关节确定腕关节的位置，故同样利用式(2)可以将系0到系3的齐次变换矩阵表示为如下形式：

(4)

由式(3)与式(4)便可确定系0到系6的齐次变换矩阵0A6=0A33A6

1.2 控制模型

利用所建焊装机器人运动学模型，在每个关节上采用一个交流伺服电机对其进行独立的PD控制，并利用电机编码器的反馈量对每个关节实现闭环位置控制。在设计实验时，采用德州仪器公司的TMS320F2812 DSP芯片对编码器信号进行实时处理，并根据SVPWM(Space Vector Pulse Width Modulation)调制原理[4]，利用空间矢量脉宽调制产生电机的控制信号控制交流伺服电机。同样的，如果采用具有固定重力补偿的PD控制或者利用计算力矩法改进控制方案时，也可以利用DSP强大的实时计算能力对系统进行补偿计算，并实时修正所调制出电机的SVPWM调制波，通过改变对交流伺服电机的各相电枢电压通断时间实现对电机的速度控制，并在相对低的速度下使电机转动到期望位置。当采用独立的PD控制模型时，根据机器人的动力学模型[5]：

(5)

(6)

其中，H*为系统的哈密尔顿函数，q为机器人在广义坐标下的冲量形式，τ为采用具有固定重力补偿的PD控制时的定点控制，由LaSalle定理可知，当有下式成立时：

(7)

图3 具有固定重力补偿控制模型Fig.3 Control model with fixed gravity compensation

2 模型求解

2.1 求解关节控制量

针对六自由度焊装机器人，利用所建模型，求解相应各关节的控制量q=[q1,…,q3,θ4,θ5,θ6]，根据文献[6]知，若机器人后3个关节轴线始终交于一点，则所建机器人各个关节量存在解析解。当给定工件坐标系的齐次变换矩阵时，便可求解对应各关节的控制量，在所建模型中，当式(1)为已知时，便可求解出各关节量的解析表达式，当将表达式的自变量写成与时间的函数时，机器人便在工作空间里沿着连续轨迹运动，根据计算出的关节控制量，以实时对各个关节电机进行追踪和调速。根据文献[7]提供的方法，求解机器人逆运动学模型中的各个关节控制量，由式(1)知

(8)

其中0x6，0y6分别为X6轴和Y6轴上单位矢量x6，y6在系0中每个坐标轴上的表达式，根据式(9)可以求出：

0p5=0p6-d60z6≜[px,py,pz]T

(9)

其中0p5即是机器人腕关节在系0中的位置表达式，在齐次变换矩阵0A5中，第四列的前3个元素分别对应px,py，px,则根据式(2)得：

(10)

要利用式(10)求得q1,q2,q3，根据机器人的结构特点及D-H参数知：

即

(11)

根据式(11)先求解c3,s3如下：

(12)

从而得出：

(13)

令a=(a2+d4s3)，b=d4c3,最后计算出第二个关节的控制量得：

(14)

利用式(14)相除便可解得第二个关节的控制量：

(15)

根据机器人齐次变换矩阵的第四列元素解出前3个关节的控制量之后，由于机器人各关节满足存在解析解的条件[8]，根据齐次矩阵的前三列元素便可确定后3个关节的控制量，即是由机器人工件坐标系的指向确定后3个关节的控制量。由文献[5]知：任一方向余弦阵等于3个基本旋转矩阵的乘积。齐次矩阵式(1)与式(9)均包含机器人工件坐标系的方向余弦阵0R6，3个基本旋转矩阵分别为绕z轴旋转φ的Rz(φ)，绕y轴旋转θ的Ry(θ)以及绕x旋转φ的Rx(φ)，其中{φ,θ,φ}依次对应关节4、关节5、关节6的控制量q4、q5、q6，利用齐次矩阵前三行三列元素的一一对应的关系便可解出后3个关节的控制量：

(16)

至此，已全部得出机器人所有6个关节控制量q。当要求机器人在t=0时从起始位置q=0沿工具坐标系Oξηζ的Z轴方向经过2 s平移100 mm到达期望位置qf时，可通过使其跟踪t的5次多项式表示的时变期望轨迹qd(t)来实现：

(17)

解得时变轨迹如图4所示。

图4 机器人对时变轨迹的追踪Fig.4 The time-varying trajectory tracking of robot

2.2 求解控制模型

表2 机器人各杆惯性参数

用机器人各杆对其D-H坐标系的惯性参数，便可求出：

(18)

从而求解出式(6)中的3个系数矩阵，然后反代入求出控制机器人各个关节的力矩：

(19)

其中i,j,k=1,2,3,4,5,6，机器人的位姿由关节量q确定后，每个关节作动器输出力矩τ便由式(6)和式(19)计算出来了，这便是控制机器人运动的基本力矩，具有非线性强耦合性，且由于控制电机的调速特性，所以利用电机调速和控制时，需建立补偿使系统反馈线性化，并要求对位置增益足够大以确保系统对时变轨迹跟踪及定点控制具有一定的稳定性。

2.3 验证控制模型

利用机器人的动力学分析，可以得出控制机器人关节电机的基本动力要求，如果计入各个关节的摩擦转矩与电机的质量和惯性参数，则必须增加电机动力输出裕度，与此同时，在利用DSP对电机及编码器反馈信号进行实时闭环控制时，必须考虑电机的过流和过压问题，所以控制环内还必须设置对电流和电压的反馈检测，并考虑机器人启停时电流电压冲击，在机器人关节空间内进行定点运动时，必须利用DSP对关节电机进行S型加减速控制。伺服电机通常可以是电压调速或电流调速的，如果采用电流调速，且电机转矩常数为Km，电流常数为Ki，转动惯量为Jm，减速器减速比为G，电机黏性摩擦系数为Bm，则独立关节控制满足：

(20)

其中u为系统输入，ω为电机的角速度，τc为电机最大转矩，对式(20)进行拉普拉斯变换并改写成线性表达式：

(21)

采用比例微分对速度环进行反馈控制时，必须考虑重力对关节的扭矩，所以加入积分项使系统的输入为

(22)

其中Kv、Ki分别为速度增益和位置增益，利用独立关节控制模型，针对不同的控制要求，便可得出系统响应曲线。系统的控制框图如图5所示。

图5 关节电机独立控制模型Fig.5 Joint motor independent control model

在Simulink环境下验证控制模型，利用信号发生器分别产生三角波和矩形波模拟关节期望输入轨迹，与实际输出轨迹相减后，对信号延迟0.01 s输入到积分器并获得增益，从而模拟位置反馈量，加上速度反馈量后一起送入电机，此外，通过限定输入控制信号上下限以模拟电机的转矩范围，重力对关节控制的影响随着机器人位姿的变化而变化，为了对其进行模拟，在模型中引入前馈环节，即设定一常值输入ff_Con，并根据减速器的减速比G获得增益后，计入到关节控制量，在考虑电机过流及过压保护并引入安全系数k后，控制模型对锯齿波及矩形波的响应曲线如图6所示。

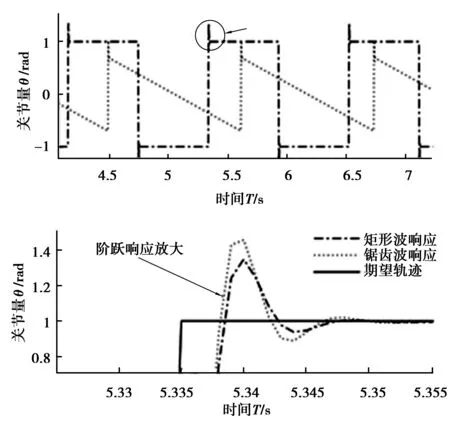
图6 系统对锯齿波及矩形波的追踪及响应Fig.6 Tracking and response of saw tooth and rectangular wave

3 仿真实验及结论

六自由度焊装机器人运动学及动力学模型的研究，利用了两个重要工具：SIMENS PLMTecnomatix上位机软件及DSP下位机控制系统。首先，在MATLAB环境下求解机器人逆运动学模型及各轴空间运动插补的连续坐标值，以实现机器人工件坐标系对特定轨迹的插补运动，结果表明：在没有通过示教而直接利用本研究模型中的数值算法控制机器人运动时，计算量较大且不适合用于后续的动力学控制；其次，在Tecnomatix环境下创建了一个四机器人协同焊接工位，同时利用其针对特定机器人厂家开发的离线虚拟仿真调试RCS(Robot Control System)模块，对机器人进行虚拟示教并得出各轴关节控制量，在此基础上，利用所研究的独立关节控制模型，对机器人的两个关节实施带有重力补偿的动力学控制，图6表明：对机器人单个关节电机，响应时间大约为0.08 s，随后达到期望轨迹，但对阶跃响应的超调量较大，约为期望值的30%左右，基本满足独立关节控制的要求，且可以通过改变系统增益来提高控制精度，但降低了系统稳定性。最后，在获得期望轨迹在各轴空间的连续坐标值且满足独立关节控制的动力学要求之后，为了满足机器人6个关节电机的实时控制要求，引入了DSP下位机控制系统，其对电机调速使用的SVPWM调制波生成程序及编码器反馈信号处理程序均在CCS环境下开发，并通过片上事件管理器实现各关节编码器信号实时处理以及关节电机实时控制，结果表明：通过虚拟示教或基于运动学模型数值解算所获得的关节控制量，均能在DSP下位机控制系统上实现对机器人的实时控制。运动学仿真及独立关节控制实验如图7所示。

图7 Tecnomatix环境下仿真与实验Fig.7 Simulation and experiment using tecnomatix

[1] DRAKE B W.Implementation of a Unified Robot Kinematics and Inverse Dynamics Algorithm on a DSP Chip[J].Industry Electronics,1993,40(2):273-281

[2] KABUKA M,ESCOTO R.Real-time Implementation of the Newton-Euler Equations of Motion on the NEC μ PD77230 DSP[J].Micro,1989,9(1)：66-76

[3] PETER I C.Robotics,Vision and Control[M].Australia:Queensland University of Technology,2010

[4] 欧阳名三.DSP原理与技术[M].合肥:合肥工业大学出版社,2009

OUYANG M S.DSP Principle and Technolgy[M].Hefei:Hefei University of Technology Press,2009

[5] 霍伟.机器人动力学与控制[M].北京:高等教育出版社,2005

HUO W.Robot Dynamics and Control[M].Beijing:Higher Education Press,2005

[6] LASALLE J,LEFSCHETZ S.Stability by Lyapunov’s Direct Method[M].New York:Academic Press,1961

[7] PAUL R P.Modeling,Trajectory Calculation and Servoing of a Computer Controlled Arm[G].Stanford Artificial Intelligence Laboratory Memo AIM177,1972

[8] 彭启琮.DSP集成开发环境[M].北京:电子工业出版社,2004

PENG Q Z.DSP Integrated Development Environment[M].Beijing:Publishing House of Electronics Industry,2004

[9] TISAN A,CIRSTEA M.SOM Neural Network Design—a New Simulink Library Based on Approach Targeting FPGA Implementation[J].Mathematics and Computers in Simul-ation,2013,91(10):134-149

[10] MATTEO P.Static Performance Improvement of an Industrial Robot by Means of a Cable-driven Redundantly Actuated System[J].Robotics and Computer-Integrated Manufacturing,2016,38(c):1-8

[11] SAMANTHA V A,THOMAS W,SUE D.Adaptive Training of Cortical Feature Maps for a Robot Sensorimotor Controller[J].Neural Networks,2013,44(8):6-21

[12] SAVKIN A V,WANG C,BARANZAHEH A.Distributed Formation Building Algorithms for Groups of Wheeled Mobile Robots[J].Robotics and Autonomous Systems,2016,75(PB):463-474

[13] GUO Q,PERUQUETTI W,EFIMOV D.Universal Robot Adaptive Control of Robot Manipulators Using Real-Time Estimation[DB/OL].IFAC-PapersOnLine,2015

[14] GROSSARD M.Robust Decentralized Control of a Fully Actuated Robot Hand[DB/OL].IFAC-Papers OnL-ine,2015

[15] DANEVIT J,HARTENBERG R S.A Kinematic Notation for Lower-pair Mechanisms Based on Matrices[J].ASME Journal of Applied Mechanits,1995,22:215-221

[16] PIEPER D L.The Kinematics of Manipulations under Computer Control[D].Palo Alto:Stanford University,1968

[17] ARIMOTO S,MIYAZAKI F.Stability and Robustness of PID Feedback Control for Robot Manipulator of Sensory Capability[C]∥The First Int Symposium: Robotics Research,1983:783-799

[18] 高名旺.3RRR高速并联机器人运动学设计与实验[J].机器人,2013,35(6):716-722

GAO M W.Experiment and Kinematic Design of 3-RRR Parallel Robot with High Speed[J].ROBOT,2013,35(6):716-722

[19] 孟石.多机器人协作系统轨迹约束分析及示教方法[J].机器人,2012,34(5),547-565

MENG S.Path Constraint Relation and Trajectory Teaching Method for Multi-Robot Cooperation System[J].ROBOT,2012,34(5),547-565

[20] 陈鹏.一种仿人机械臂的运动学逆解的几何求解方法[J].机器人,2012,34(2),212-216

CHEN P.A Geometrical Method for Inverse Kinematics of a Kind of Humanoid Manipulator[J].ROBOT,2012,34(2),212-216

责任编辑：罗姗姗

Research and Simulation of Control Algorithm Design of Welding Robot Based on DSP

DENG Shun1,2, ZHOU Kang-qu1

(1. College of Mechanical Engineering, Chongqing University of Technology, Chongqing 400054, China;2. Changan Automobile Intelligent Manufacturing Technology Research Institute, Chongqing 401120, China)

Based on the establishment of six DOF welding robot D-H coordinate system and the parameters of the arms, the forward kinematics and inverse kinematics equations are studied and its numerical simulation algorithm is designed and simulation model in MATLAB environment is also designed, and the control of each joint motor under the fixed control mode and fixed gravity compensation is also obtained. On the basis of the dynamic control equation of six DOF robot, the consideration of the characteristics of the motors and the dynamic characteristics of the robot arm are also obtained, and the optimization model of sensor feedback control is established. The four robot welding station in Tecnomatix environment is created, Using the Robotics function module provided, the path and function of the robot are realized. The Newton Euler inverse kinematics equations of the digital signal processor are used to solve the robot’s joint coordinate and to process the sensor feedback signal in real-time, and to realize the closed-loop control of the multi servo system.

forward and inverse dynamics of robots; DSP; real-time control

10.16055/j.issn.1672-058X.2017.0001.017

2016-09 -19；

2016-10-20.

国家重大科技专项《长安汽车城节能与新能源汽车智能柔性焊接新模式应用项目》.

邓顺(1988-)，男，重庆奉节人，硕士，从事机器人控制系统研究. E-mail: 15123376162@163.com.

TH692.9

A

1672-058X(2017)01-0087-07