非参数混合效应模型的估计*

阙 烨

(南京理工大学 理学院，南京 210094)

非参数混合效应模型的估计*

阙 烨

(南京理工大学 理学院，南京 210094)

针对非参数混合效应模型提出估计方法，通过B样条的方法估计非参数函数，使用惩罚(非加权)最小二乘方法估计随机效应，然后通过构造正态似然函数得到方差的估计，并且证明了方差分量的相合性和函数部分的渐近正态性；最后给出数字模拟来展示所提出方法的估计效果，结果表明：该方法给出的估计效果良好，且在数值上是稳定的。

非参数混合效应模型；B样条；惩罚最小二乘；正态似然函数

1 基础知识

在分析相关数据的时候经常用到混合效应模型，因此此处考虑非参数混合效应模型：

(1)

混合效应模型对于分析纵向和重复测量数据来说是一个重要工具，近年来它引起了国内外统计学者的极大关注。Cai T,etal.(2002)[1]研究了在集群故障时间数据下的半参数混合效应模型，他们在文中提出了对于这个随机效应模型的推断和预测；Chen Z和Dunson D(2003)[2]研究了线性混合效应模型的随机效应选择；Li W B和Xue L G(2014)[3]研究了广义部分线性混合效应模型的有效推断问题，他们对参数和方差分量提出了一系列半参数估计值，然后使用局部线性光滑方法去展示非参数分量的估计值；Pang Z和Xue L G(2012)[4]研究了单指标混合效应模型，为了估计指标系数和联系函数，提出了一系列新的估计方程去调整边界效应，使用局部线性光滑方法去估计非参数函数；Schimek M G(2000)[5]研究了部分线性模型在光滑样条下的估计和推断，描述了在光滑样条方法下的廉价直接算法，光滑参数可以被选择通过一个无偏风险标准；Zhong X P,etal.(2003)[6]对带有变量误差的线性混合效应模型的估计提出了统一分类法；Zhao H B和You J H(2011)[7]研究了带有测量误差的部分线性回归模型的不同估计，他们给出的估计是渐近无偏估计并且实现了非参数有效边界。其他的关于随机效应的文献可参看Li W B和Xue L G(2013)[8]，Liang H(2009)[9]，Lindstrom M J和Bates D M(2010)[10]，Wu H和Zhang J T(2002)[11]。此处与已有文献的不同之处是本文使用B样条来估计函数部分，从而将非参数模型转化为线性混合效应模型。B样条估计方法的优点在于它有紧支撑，这使得计算速度加快，函数部分的拟合曲线会更光滑，这无疑在视觉上更吸引人。而随机效应项的处理借鉴了已有文献的方法并在此基础上进行改进，请参考文献Gu C和Ma P(2005)[12]。

2 估计方法

2.1 非参数函数的估计

使用B样条基函数将g(·)表示为

2.2 随机效应项b的估计

这里使用惩罚最小二乘法估计b，极小化

(2)

2.3 方差分量的估计

-n(n-1)log(σε2)-nlog(σε2+nσb2)-

3 主要结果的证明

首先，给出下列条件：

Ⅰc0表示一个常数，有E(e2)≤c0<∞成立，这里e=Zb+ε=Y-g(U)；

Ⅱ 对任意的i，协变量Ui是独立同分布的变量，且Ui的分布是紧支撑集；

定理2 在条件(Ⅰ)—(Ⅲ)下，有

(3)

(4)

定理1的证明 定理1的证明类似于Huang J Z,etal.(2004)[13]中定理2的证明方法，这里忽略该定理的证明过程。

定理2的证明 先证明式(3)。

下面证明式(4)，进行一系列的演算后有：

N2=OP(n-1/2)

N3=OP(n-1/2)

通过利用式(3)就得到了式(4)的证明。

4 数值模拟研究

例1 考虑模型:Yi=cos(πUi)+b+εi,i=1,2,…,n,其中Ui服从区间(0,1)上的均匀分布，模型的随机效应项服从均值为0，方差为0.16的正态分布，误差项服从均值为0，方差为0.04的正态分布的随机变量。运用B样条估计函数项，本例中样条的节点由广义交叉验证(GCV)方法得出节点个数为5个，样条阶数为3。

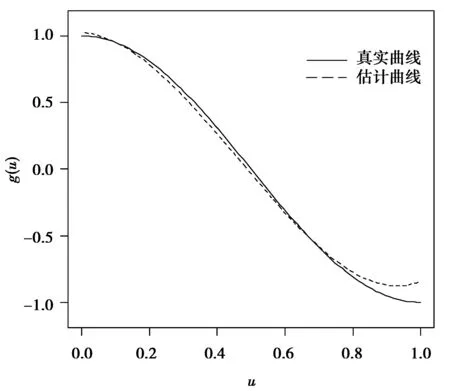
图1 函数部分的真实曲线和估计曲线(n=100)Fig.1 The real link function curve and the estimated link function curve(n=100)

图2 函数估计值的箱线图(n=100)Fig.2 The boxplot for the estimated link function(n=100)

[1] CAI T,CHENG S C,WEI L J.Semiparametric Mixed-effects Models for Clustered Failure Time Data[J].Journal of the American Statistical Association,2002,97(6):514-522

[2] CHEN Z,DUNSON D.Random Effects Selection in Linear Mixed Models[J].Biometrics,2003,59(4):762-769

[3] LI W B,XUE L G.Efficient Inference in a Generalized Partially Linear Model with Random Effect for Longitudinal Data[J].Communication in Statistics Theory and Methods,2014,44(2):241-260

[4] PANG Z,XUE L G.Estimation for the Single-index Models with Random Effects[J].Computational Statistics and Data Analysis,2012,56(6):1837-1853

[5] SCHIMEK M G.Estimation and Inference in Partially Linear Models with Smoothing Splines[J].Journal of Statistical Planning and Inference,2000,91(2):525-540

[6] ZHONG X P,FUNG W K,WEI B C.Estimation in Linear Models with Random Effects and Errors-in-variables[J].Annals of the Institute of Statistical Mathematics,2002,54(3):595-606

[7] ZHAO H B,YOU J H.Difference Based Estimation for Partially Linear Regression Models with Measurement Errors[J].Journal of Multivariate Analysis,2011,102(10):1321-1338

[8] LI W B,XUE L G.Efficient Inference about the Partially Linear Varying Coefficient Model with Random Effect for Longitudinal Data[J].Communications in Computer and Information Science,2013(391):573-583

[9] LIANG H.Generalized Partially Linear Mixed-effects Models Incorporating Mismeasured Covariates[J].Annals of the Institute of Statistical Mathematics,2009,61(1):27-46

[10] LINDSTROM M J,BATES D M.Nonlinear Mixed-effects Models for Repeated Measures Data[J].Biometrics,2010,46(46):673-687

[11] WU H,ZHANG J T.Local Polynomial Mixed-effects Models for Longitudinal Data[J].Journal of the American Statistical Association,2002,97(459):883-897

[12] GU C,MA P.Optimal Smoothing in Nonparametric Mixed-effect Models[J].Annals of Statistics,2005,33(3):1357-1379

[13] HUANG J Z,WU C O,ZHOU L.Polynomial Spline Estimation and Inference for Varying Coefficient Models with Longitudinal Data[J].Statistica Sinica,2004,14(3):763-788

责任编辑：李翠薇

The Estimation for the Nonparametric Mixed Effects Model

QUE Ye

(School of Science, Nanjing University of Science and Technology, Nanjing 210094, China)

The estimation methodology for the nonparametric mixed effects model is proposed. For this, we use the B-splines methods to estimate the function, and employ the penalized least square method to obtain the estimator of the random effects. Further, we construct the normal likelihood function to estimate the variance components. And we also prove the consistency of variance components and the asymptotic normality of the link function.A simulation study is carried out to show the estimation effect of our proposed methodology.It shows our proposed methodology performs well.Our algorithm is stable numerically.

nonparametric mixed effects model; B-splines method; penalized least square method; normal likelihood function

10.16055/j.issn.1672-058X.2017.0000.003

2016-05-19；修回时间：2016-06-24.

江苏省自然科学基金(BK20131345).

阙烨(1992-)，女，安徽淮南人，助教，硕士研究生，从事非参数统计及应用研究.

O212.7

A

1672-058X(2017)01-0010-04