永磁同步电动机模型的动力学研究及其数值仿真

张 光 云

(重庆工商大学 数学与统计学院,重庆 400067)

永磁同步电动机模型的动力学研究及其数值仿真

张 光 云

(重庆工商大学 数学与统计学院,重庆 400067)

在已有文献研究的基础上，利用微分方程与动力系统的基本理论与方法，首先从解析上推导出永磁同步电动机混沌模型的全局吸引域，然后对这个理论结果进行仿真；理论分析及数值仿真结果表明：该永磁同步电动机混沌模型全局吸引集的研究结果是正确的； 研究结果对保证电机传动系统的稳定运行具有较好的参考价值；同时，为永磁同步电动机混沌系统在工程中的应用和电路设计提供了理论依据。

永磁同步电动机；混沌吸引子；全局吸引域；工程应用

混沌一词来源于希腊，意味着非预测性，混沌是有序和无序的统一[1]。混沌无处不在，人们并不陌生，它存在于非线性科学领域的很多分支，如物理学、生物学、化学、电子学、医学、生命科学、神经网络、复杂网络、金融学、经济学、社会学等。很多专著从多个角度来研究混沌系统的性质及其在非线性科学领域中的应用[1-10]。1977年,在意大利召开了有关混沌的首次国际学术会议,从而混沌控制的研究正式在全球开始。1990年,德国专门举行了关于混沌分岔的学术会议。1984年,郝柏林院士[2]专著《chaos》出版，书中系统地介绍了有关混沌的前沿学术成果。在数学上存在一些研究混沌系统动力学性质的方法,例如Bifurcation图、Poincare映射、Poincare截面、平衡点的局部拓扑类型、周期解的存在性和稳定性、同宿规、异宿轨的存在性和保持性等[11-13]。

鉴于混沌系统重要的应用价值，此处将研究一个永磁同步电动机混沌模型，以便为该永磁同步电动机混沌系统在工程中的应用提供理论依据。

1 动力系统模型

经过变换的均匀气隙永磁同步电动机的数学模型为[14]

(1)

式(1)中，x1,x2,x3为无量纲状态变量，分别为d轴定子电流、q轴定子电流和转子机械角速度;ud,uq和TL分别为d轴定子电压、q轴定子电压和负载扭矩；γ>0和σ>0为系统参数。

当ud=uq=TL=0时，可以看作是永磁同步电动机空载运行一段时间后突然断电，外部输入项为零的情形，此时永磁同步电动机的数学模型为[14]

(2)

其中γ>0,σ>0为系统(2)的参数，当σ=4,γ=50时，系统(2)进入混沌状态,混沌吸引子见图1(图1中x,y,z分别代表x1,x2,x3)。

图1 系统(2)在三维空间中的混沌吸引子Fig.1 Chaotic attractor of system (2) in the 3D space

2 全局吸引域

定理1 对任意的∀γ>0,σ>0,令

θ=min{σ,1}>0

X(t)=(x1(t),x2(t),x3(t))

X(t0)=(x1(t0),x2(t0),x3(t0))

则当V(X(t))≥L,V(X0)>L(t≥t0)时，系统(1)的正半轨线有估计式：

V(X(t))-L≤[V(X(t0))-L]e-θ(t-t0)

从而,

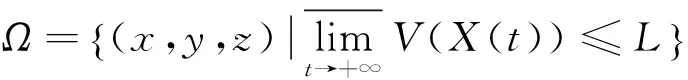
(3)

为永磁同步电动机系统(1)的一个全局指数吸引集。

证明 记函数:

则有

作广义Lyapunov函数：

当V(X(t))≥L,V(X0)>L(t≥t0)时,计算V(X(t))对时间t的导数:

2(x1-γ-σ)(-x1+x2x3+ud)+

2x2(-x2-x1x3+γx3+uq)+2x3[σ(x2-x3)-TL]=

2uqx2-2TLx3-2(γ+σ)ud=

g(x3)+(γ+σ)2-2(γ+σ)ud≤

-θV(X)+θL≤-θ(V(X)-L)<0

(4)

当V(X(t))≥L,V(X0)>L(t≥t0)时，对不等式(4)两边积分：

V(X(t0))e-θ(t-t0)+L(1-e-θ(t-t0))

(5)

整理得：

V(X(t))-L≤[V(X0)-L]e-θ(t-t0)

(6)

令不等式(6)两边t→+∞,取上极限：

从而，

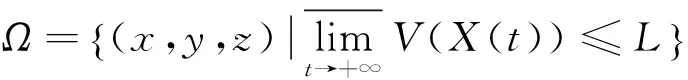
为永磁同步电动机系统(1)的一个全局吸引集。

定理2 对任意的∀γ>0,σ>0,令

X(t)=(x1(t),x2(t),x3(t))

X(t0)=(x1(t0),x2(t0),x3(t0))

则当V(X(t))≥L0,V(X0)>L0(t≥t0)时，系统(2)的正半轨线有估计式：

V(X(t))-L0≤[V(X(t0))-L0]e-θ(t-t0)

从而,

(7)

为永磁同步电动机系统(2)的一个全局指数吸引集.

证明 证明方法与定理1的证明方法类似.

图2 系统(2)的轨线最终进入Ω1,1之内Fig.2 The trajectory of system (2) finally enters into Ω1,1

3 结 论

研究了永磁同步电动机混沌系统的全局吸引性，研究方法适用于其他混沌系统的研究,研究结果对电机传动系统的混沌控制的应用将起到一定的参考价值。

[1] 闫振亚.复杂非线性波的构造性理论及其应用[M].北京: 科学出版社,2002

YAN Z Y.The Complex Nonlinear Wave Structure Theory And Its Application[M].Beijing:Science Press,2002

[2] HAO B L.Chaos[M].Singapore:World Scientific,1984

[3] DOEDEL E J,KRAUSKOPF B,OSINGA H M.Global Organization of Phase Space in the Transition to Chaos in the Lorenz System[J].Nonlinearity,2015,28(11):113-139

[4] MESSIAS M.Dynamics at Infinity and the Existence of Singularly Degenerate Heteroclinic Cycles in the Lorenz System[J].Journal of Physics A:Mathematical and Theoretical,2009,42(11):12-30

[5] LEONID A B.Short-and Long-term Forecast for Chaotic and Random Systems (50 Years after Lorenz’S Paper)[J].Nonlinearity,2014,27:51-60

[6] SPARROW C.The Lorenz Equations:Bifurcations,Chaos,and Strange Attractors[M].Springer Science & Business Media,2012

[7] CHEN G R,UETA T.Yet Another Chaotic Attractor[J].International Journal of Bifurcation and Chaos,1999,9(7):1465-1466

[8] LU J H,CHEN G R.A New Chaotic Attractor Coined[J].International Journal of Bifurcation and Chaos,2002,12(3):659-661

[9] WANG X Y,WANG M J.A Hyperchaos Generated from Lorenz System[J].Physica A:Statistical Mechanics and Its Applications,2008,387(14):3751-3758

[10] 蒲浩,刘衍民,黄建文,等.具有非线性脉冲效应的Cohen-Grossberg型神经网络的指数同步[J].重庆工商大学学报(自然科学版),2016,33(3):1-5

PU H,LIU Y M,HUANG J W,et al.Exponential Synchronization for Cohen-Grossberg Neural Networks with Nonlinear Impulsive Effects[J].Journal of Chongqing Technology and Business University(Natural Science Edition),2016,33(3):1-5[11] ZHANG F C,MU C L,ZHOU S M,et al.New Results of the Ultimate Bound on the Trajectories of The Family of the Lorenz Systems[J].Discrete and Continuous Dynamical Systems-Series B,2015,20(4):1261-1276

[12] ZHANG F C,ZHANG G Y.Further Results on Ultimate Bound on the Trajectories of the Lorenz System[J].Qualitative Theory of Dynamical Systems,2016,15(1):221-235

[13] LIN D,ZHANG F C,LIU J M.Symbolic Dynamics-Based Error Analysis on Chaos Synchronization via Noisy Channels[J].Physical Review E,2014,90:1-7[14] 韦笃取，罗晓曙,方锦清,等.基于微分几何方法的永磁同步电动机的混沌运动的控制[J].物理学报，2006，55(1)：54-59

WEI D Q,LUO X S,FANG J Q,et al.Controlling Chaos in Permanent Magnet Synchronous Motor Based on the Differential Geometry Method[J].Acta Physica Sinica,2006,55(1)：54-59

责任编辑：李翠薇

Research on Dynamics of Permanent Magnet Synchronous Motor and Its Numerical Simulation

ZHANG Guang-yun

(School of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067, China)

On the basis of the existing literature research, this paper uses the basic theory and method of differential equation and dynamics system to firstly derive the global attraction region of the chaotic model of the permanent magnet synchronous motor and then to make simulation on the theoretical results. The theoretical analysis and numerical simulation results show that the studying result of global attraction set of the chaotic model of this permanent magnet synchronous motor is correct. The studying result has good reference value for the stable operation of the gearing system of the motor, and meanwhile, the research results provide theoretical basis for the motor to be used in circuit design and engineering of the chaotic system of the motor.

permanent magnet synchronous motor; chaotic attractor; global attractive region; engineering application

10.16055/j.issn.1672-058X.2017.0001.008

2016-09-14；

2016-10-23.

张光云(1983-),女,山东临沂人,助教,硕士,从事外国语言学及应用语言学、常微分方程的理论研究.

TP393

A

1672-058X(2017)01-0041-04