并联稳定平台电液驱动单元复合内模控制研究

张立杰 王力航 李少华 李永泉

1.燕山大学河北省重型机械流体动力传输与控制重点实验室， 秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，0660043.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004

并联稳定平台电液驱动单元复合内模控制研究

张立杰1,2王力航1李少华1李永泉2,3

1.燕山大学河北省重型机械流体动力传输与控制重点实验室， 秦皇岛，0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，0660043.燕山大学河北省并联机器人与机电系统实验室，秦皇岛，066004

针对液压驱动舰船稳定平台样机的运动控制要求，提出了一种基于速度前馈结构的复合内模控制方案。以舰船稳定平台的单通道液压驱动单元为研究对象，采用机理建模和参数辨识相结合的方法得到了控制对象的数学模型，在模型的基础上完成了基于速度前馈结构内模复合控制器的设计，并对提出的控制方法进行了仿真和实验研究。仿真和实验研究结果表明：基于速度前馈结构的复合内模控制可以改善系统的跟踪性能，提高系统的抗干扰性和鲁棒性。

舰船稳定平台；液压驱动单元；速度前馈结构；复合内模控制

0 引言

液压伺服驱动以其大功率质量比、高频率响应成为大负载并联稳定平台的理想驱动方式。国内外学者针对液压驱动并联机构的控制问题已进行了大量研究，按照控制策略实现方法的不同，液压驱动并联机构的控制问题可以分为基于性能的控制和基于模型的控制两类。基于性能的控制常见于工业控制，如常见的PID控制。PID控制不需要知道控制对象的具体模型，工程师通过反复调节参数使并联机构运动达到设定要求。PID控制在许多实际应用场合虽然能够获得较高的位置控制精度，但是对于液压驱动的多分支并联机构而言，各执行分支间运动的耦合会导致机构出现抖振、失稳现象，从而影响控制品质，所以，对于舰船稳定平台，不仅要求高的稳态精度，也要求各个执行分支运动过程中的速度满足要求。基于模型控制方法为进一步提高并联机构跟踪性能提供了可能。文献[1-3]分别采用逆动力学模型、模型自适应算法、反馈线性化解耦方法来实现液压驱动并联机构的轨迹跟踪控制。这类方法中控制对象的数学模型通常求解过程复杂，且系统的控制品质往往会由于给定轨迹发生变化而难以保障，在需要实时随动的稳定平台系统中实现难度较大。为了提高液压驱动并联机构的跟踪性能，以液压驱动的舰船稳定平台样机液压驱动单元为研究对象，笔者提出了一种参数整定方便、易于实现的基于速度前馈结构的复合内模控制策略，并通过仿真和实验验证了该方法的有效性。

1 液压驱动单元建模

舰船稳定平台是一种用来隔离海浪运动的装备，在测量跟踪及现代武器装备中有着广泛的应用。针对海上大型舰载雷达、火炮及导弹发射平台等特种需要，基于空间并联机构承载大、精度高、易于实现多轴联动、动态响应快速等诸多优点，笔者设计了一种三自由度舰船稳定平台，平台结构如图1所示。考虑到占用空间及制造成本等因素，舰船稳定平台的液压执行单元设计为非对称伺服液压缸。

图1 舰载稳定平台结构Fig.1 Structure of ship stable platform

四通滑阀控制非对称液压缸的基本原理如图2所示。并假设：伺服阀的开口形式为零开口，四个节流边对称，恒压供油，回油压力为常压；伺服阀与液压缸间的管路短而粗，液压缸同一侧油腔中的压力处处相等；液压缸的内外泄漏均为层流；系统的油温和体积弹性模量为常值；忽略外泄漏。

图2 四通伺服阀控制非对称液压缸原理图Fig.2 Schematic for asymmetric cylinder with four way servo valve

图2中，xv为伺服阀阀芯的位移，y为液压缸活塞杆位移，ps、pT分别为供油压力和回油压力，p1、qV1分别为无杆腔的压力和流量，p2、qV2分别为有杆腔的压力和流量，A1、A2分别为液压缸无杆腔和有杆腔有效面积，n=A2/A1为两腔有效面积之比，m为活塞及折算到活塞上面的质量，FL为外负载力，B为伺服油缸的黏性阻尼系数，KL为负载的弹簧刚度。

1.1 系统负载压力及负载流量定义

负载流量及负载压力定义方法是阀控非对称缸系统研究中的热点讨论问题[4-6]，现定义如下：

(1)当xv>0时，伺服液压缸的活塞杆外伸，即dy/dt>0，则有伺服液压缸和负载力平衡方程：

p1A1-p2A2=FL

(1)

定义负载压力

pL=p1-np2

(2)

则伺服液压缸的输出功率

pout=p1qV1-p2qV2=pLqV1

(3)

此时，为了使阀控非对称伺服液压缸系统的输出功率与输入功率匹配，定义负载流量qVL=qV1。

(2)当xv<0时，伺服液压缸的活塞杆缩回，即dy/dt<0，则有伺服液压缸和负载力平衡方程：

p2A2-p1A1=FL

(4)

定义负载压力

pL=p2-p1/n

(5)

则伺服液压缸的输出功率

pout=p2qV2-p1qV1=pLqV2

(6)

此时，为了使阀控非对称伺服液压缸系统的输出功率与输入功率匹配，定义负载流量qVL=qV2。

1.2 活塞缸外伸时阀控缸系统模型

(1)四通对称滑阀的流量方程：

(7)

(8)

(9)

式中，Cd为伺服阀口的流量系数；ρ油液密度；w为伺服阀阀口面积梯度。

(2)伺服液压缸的流量连续方程。流入伺服液压缸有杆腔的流量

(10)

流出伺服液压缸无杆腔的流量

(11)

式中，Cip为伺服液压缸内部漏损系数；βe为液压油的容积模数；V1为伺服液压缸无杆腔的容积；V2为伺服液压缸有杆腔的容积。

伺服液压缸的工作容腔体积还可以表示为

V1=V10+A1y

(12)

V2=V20-A2y

(13)

式中,V10为伺服液压缸无杆腔初始压缩容积；V20为伺服液压缸有杆腔初始压缩容积。

由式(2)、式(7)、式(8)可以得到伺服液压缸容腔的压力表达式：

(14)

整理式(1)、式(2)、式(10)、式(12)、式(14)可以得到活塞杆外伸时伺服液压缸的流量连续方程：

(15)

Cie=(1+n2)Cip/(1+n3)

Cta=n2(1-n)Cip/(1+n3)

Vt=4V1/(1+n3)

式中，Cie为伺服液压缸等效漏损系数；Cta为液压缸附加漏损系数；Vt为伺服液压缸等效压缩容积。

(3)伺服液压缸和负载的平衡方程:

(16)

(4)伺服阀阀口流量线性化方程：

qVL=Kqxv-KcpL

(17)

式中，Kq为综合流量增益；Kc为综合压力增益。

为了便于分析，对模型作出部分简化。舰船稳定平台样机的负载为惯性负载，不考虑弹性负载的情况，即KL=0。联立式(15)～式(17)，并进行拉氏变换，在不引起歧义条件下，频域信号采用对应时域信号大写表示，则可以得到系统传递函数：

(18)

Kce=Kc+Cie

式中，wh1为液压缸伸出时固有频率；ξh1为液压缸伸出时液压阻尼比；Kce为综合压力流量系数。

1.3 活塞缸缩回时阀控缸系统模型

(1)滑阀的流量方程：

(19)

(20)

(2)参考活塞杆外伸的推导过程，可以得到伺服液压缸缩回运动时的传递函数：

(21)

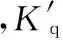
1.4 伺服阀及其他环节数学模型

结合具体实验设备分析，将伺服阀看作二阶振荡环节[7]，即

(22)

式中，Ksvi为电液伺服阀的流量增益，液压缸伸出时取Ksv1，缩回时取Ksv2；wsv为电液伺服阀的频宽；ξsv为电液伺服阀的阻尼比。

此外，舰船稳定平台液压驱动单元单通道分支上还存在伺服放大器环节、控制器环节和位移传感器环节。其中放大器、位移传感器均看作比例环节，其比例增益分别用Kp和Ks表示。图3给出了阀控非对称液压单元单通道比例闭环控制框图。

图3 液压驱动单元位置控制系统方框图Fig.3 Block diagram for hydraulic drive unit position control system

由图3可以得到阀控非对称液压单元单通道比例控制的闭环传递函数：

(23)

其中，P(s)为以阀控非对称缸系统为控制对象的传递函数：

P(s)=

(24)

2 液压驱动单元控制策略的设计及仿真研究

内模控制(internal model control ,IMC)是20世纪70年代发展起来的，基于过程数学模型进行控制器设计的先进控制策略。它的基本原理为：使用控制对象和内部数学模型的差值作为反馈信号，从而使控制对象始终逼近控制对象内部的数学模型；通过外环的闭环反馈控制来实现给定信号的准确跟踪。实践表明，内模控制具有设计简单、参数整定方便、在线调整容易等优点，能够改善系统鲁棒性和抗干扰能力[8-10]。

图4和图5分别给出了内模控制的基本结构及等效的反馈控制框图。P(s)为被控对象，M(s)为被控对象的数学模型，Q(s)为内模控制器，r为系统的输入信号，y为系统的输出响应信号，d为系统的干扰信号，D(s)为扰动对输出的影响。控制的目标是使实际输出y渐近于输入r。

图4 内模控制的基本控制结构图Fig.4 Basic control structure of internal model control

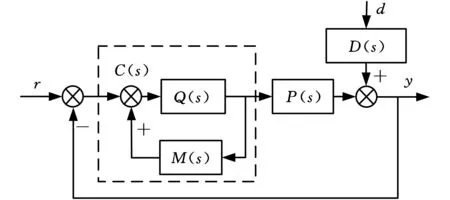
图5 等效经典反馈控制系统结构图Fig.5 Structure of equivalent classical feedback control system

根据图5所示的控制框图可以推导出内模反馈控制器的传递函数为

(25)

式(25)表明，在Q(s)=1/M(s)的内模控制器的设计原则下，系统的期望输出y与给定的输入r完全相等。内模控制的鲁棒性和抗干扰能力由此得到了体现，因为此时无论如何选择内部模型M(s)，都能获得满意的输出。为了使内部模型具有明确的物理意义，使内部模型中的参数便于调节，内部模型一般选择实际控制对象的数学模型。由于对于实际系统而言，系统模型的逆通常是不存在的，内模控制器通常由低通滤波器和控制系统的最小相位系统组成：

Q(s)=F(s)/M(s)-

(26)

F(s)=1/(1+λs)r

其中，F(s)为低通滤波器，M(s)-为M(s)最小相位部分的模型，选择适当的r来保证Q(s)为有理式，λ为内模控制器仅有的设计参数。

电液伺服控制系统高阶项的系数相对较小，同时考虑系统的稳定性、设计方便性，综合正反向运动特性，得到阀控非对称缸系统简化模型：

(27)

其中，T和K分别为系统综合惯性时间常数和系统综合增益，它们均取双向运动中较大值，即

(28)

K=max(Ksv1/A1,Ksv2/A2)

(29)

根据内模控制原理，针对式(27)所示的对象模型，取滤波器传递函数为

(30)

此时内模控制器函数为

(31)

则内模控制器传递函数为

(32)

IMC控制器的整定规则简单：减小控制器的λ值，可以提高系统的响应速度和控制精度，但是会降低系统的稳定性；反之增大λ的取值，会提高系统的稳定性和鲁棒性。内模控制相比PID控制具有更少的参数，简化了参数整定过程。由于舰船稳定平台样机各分支受外负载力影响较大，故为了满足各个分支的控制要求，λ的取值偏大，导致了内模控制的响应速度较慢，影响了稳定平台的跟踪性能。

为了改善液压伺服系统的响应速度，引入了速度前馈结构。基于前馈结构的内模控制框图见图6。

为了得到前馈通道参数τ，由线性系统叠加原理，忽略控制器作用，即令C(s)=1，则由式(24)，阀控缸系统数学模型的一般形式可以写为

图6 基于前馈结构内模控制框图Fig.6 Structure forinternal model based on feed forward

(33)

则系统传递函数为

(34)

系统误差传递函数为

(35)

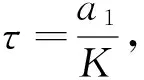
(36)

系统等效开环传递函数：

(37)

由式(37)可知，系统等效为Ⅱ型系统，此时的系统速度误差为零，加速度误差为常值，则可以实现系统的速度跟踪控制，从而提高位置控制的响应速度和控制精度[11]。由图6可以得到基于前馈结构内模控制的传递函数：

(38)

舰船稳定平台样机的控制系统组成如图7所示，包括机械系统和电液伺服控制系统两部分。在活塞和活塞杆直径分别为40 mm和25 mm，工作压力为5 MPa条件下，采用机理建模与ARX参数辨识方法相结合的建模方法[12]，获得舰船稳定平台单通道液压驱动单元参数辨识结果，如表1所示。

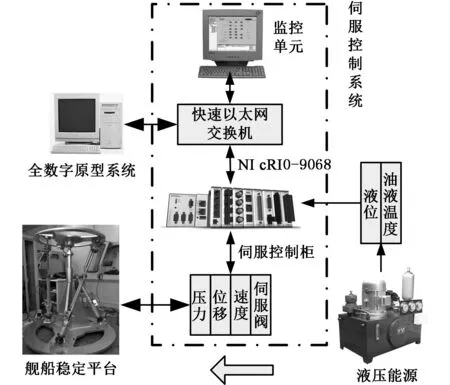
图7 舰船稳定平台的样机控制系统组成Fig.7 Compositionofship stabilized platform control system

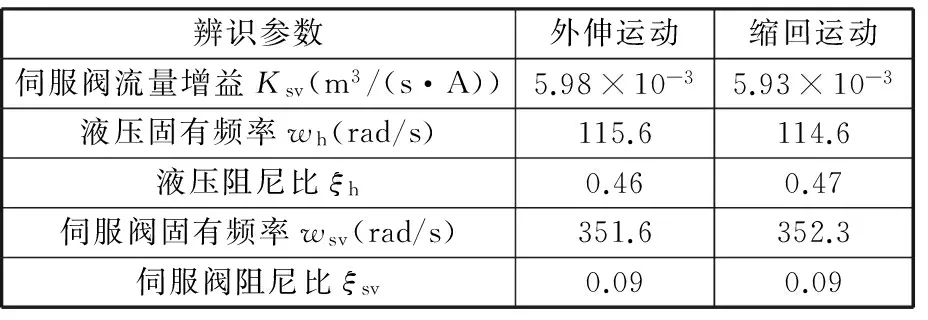
辨识参数外伸运动缩回运动伺服阀流量增益Ksv(m3/(s·A))5.98×10-35.93×10-3液压固有频率wh(rad/s)115.6114.6液压阻尼比ξh0.460.47伺服阀固有频率wsv(rad/s)351.6352.3伺服阀阻尼比ξsv0.090.09

由于所选的液压缸的内径较小且采用内置位移传感器结构，降低了无杆腔有效容积，以及连接软管较长的原因，实验过程中阀控缸系统在正反向运行时的非对称性并不明显。

综合正反向辨识结果，考虑到高阶项的系数相对较小，并由系统的稳定性和设计的方便性出发，得到单通道液压驱动单元的简化数学模型为

(39)

根据内模控制原理，针对式(39)所示的对象模型，取滤波器传递函数为

(40)

在MATLAB/Simulink中搭建舰船稳定平台单通道液压驱动单元的模型，分别采用PID算法和内模控制算法进行控制研究。采用Ziegler-Nichols方法整定PID参数：Kp=2.3，Ki=0.024，Kd=0.006。调节滤波器参数λ=0.02。给定系统单位阶跃信号，然后在t=1 s加入幅值为0.2的瞬时干扰信号。图8给出了不同控制算法下的系统响应曲线。通过对比可以发现：采用内模控制后的响应曲线响应平稳，无超调与振荡，在给定干扰后，并没有出现明显的振荡，过渡过程较为平稳。

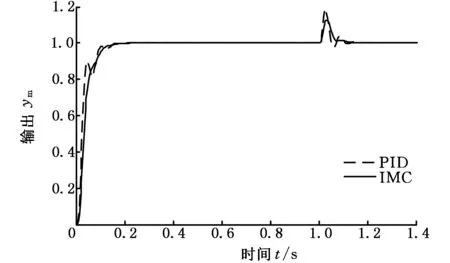
图8 不同控制方法下的系统响应曲线Fig.8 System response under different control methods

为了提高内模控制的响应速度，在原来IMC控制的基础上加入速度前馈通道。改进后的复合内模控制框图见图9。可以得出速度前馈增益为

(41)

分别在MATLAB/Simulink和AMESim中搭建基于前馈结构内模控制模型以及阀控非对称缸液压系统模型，并进行联合仿真，如图9所示。给定系统的输入信号为正弦信号，振幅为50mm，角频率为10rad/s。内模控制参数λ取为0.02。

为了便于比较分析，图9中同时搭建了内模控制(IMC)和基于速度前馈结构内模控制(复合IMC)的仿真模型，同时输入相同的正弦信号，并将响应曲线在同一坐标轴上面进行显示。图10给出了加入速度前馈结构后的内模控制正弦响应曲线。

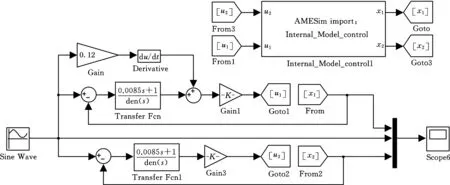
图9 基于前馈结构内模复合控制的仿真模型Fig.9 Simulation model for compound internal model control based on feedforward

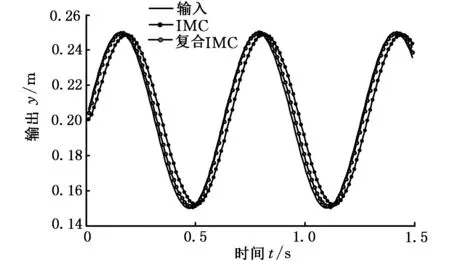
图10 基于前馈结构复合IMC控制正弦响应曲线Fig.10 Sinusoidal response curve of composite IMC control based on feedforward

由图10可以发现，单纯的内模控制策略能够准确地复现正弦信号波形，定位精度较高，但存在跟踪误差和一定的滞后。而基于前馈结构内模复合控制的正弦响应曲线，不仅具有良好的位置控制精度，而且能够快速地跟踪给定的正弦信号。

上述仿真结果说明，采用相同的内模控制参数λ，基于速度前馈结构复合内模控制方法能够在保留内模控制鲁棒性、抗干扰性等优点的前提下，提高系统的跟踪性能。

3 液压驱动单元控制策略实验研究

舰船稳定平台液压驱动系统包含三部分：液压执行单元(伺服液压缸组)、伺服阀组、液压能源以及控制系统。其中泵源流量为100 L/min，泵出口压力为5 MPa。伺服液压缸与伺服阀之间采用软管连接。采用NIcRIO-9068控制器，基于LabVIEW开发环境进行编程，实现控制算法。

当正弦信号的振幅为50 mm，频率为3 Hz时，得到的PID、IMC和复合IMC控制的正弦响应曲线分别为图11～图13。

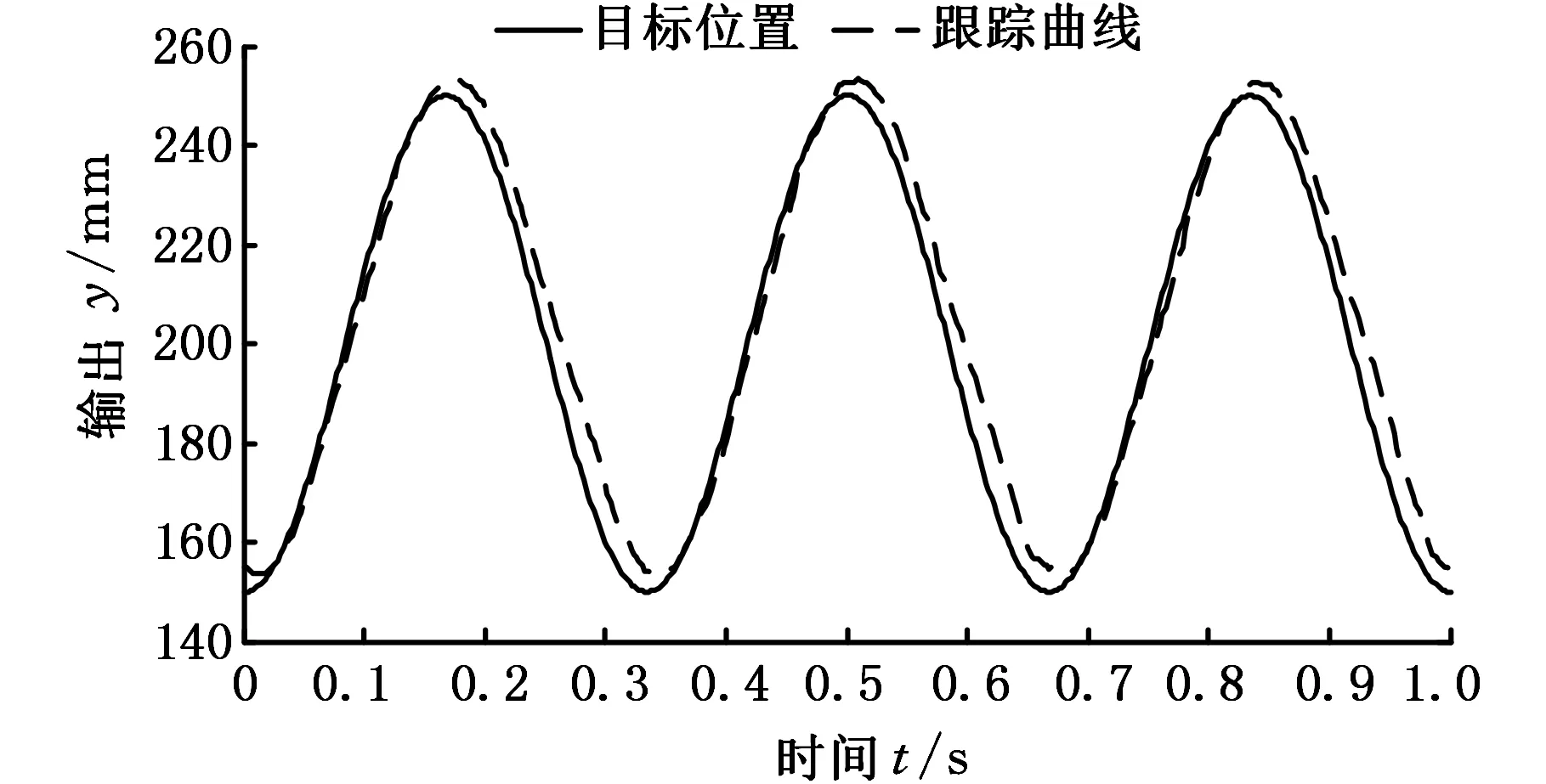
图11 PID控制正弦响应曲线Fig.11 Sine response curve with PID control

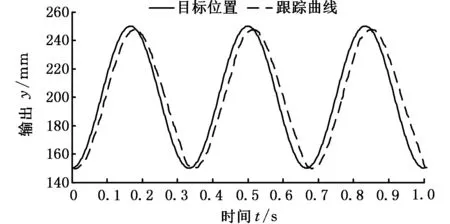
图12 IMC控制正弦响应曲线Fig.12 Sine response curve with IMC control

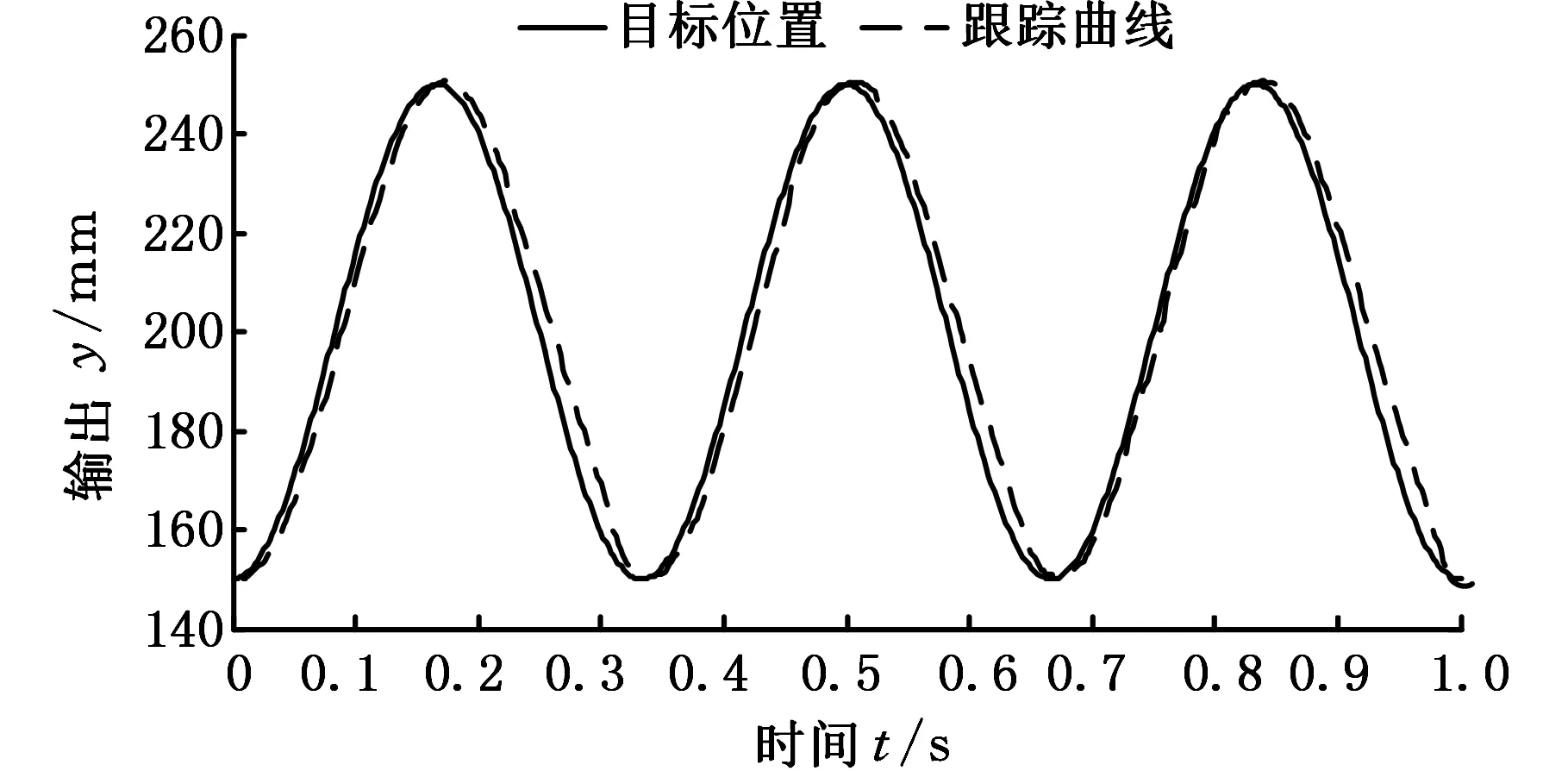
图13 速度前馈结构IMC控制正弦响应曲线Fig.13 Sine response curve with speed-forward structure IMC control

图11～13表明：对于给定的目标轨迹，PID控制输出信号存在明显超调与滞后；IMC控制能够基本复现目标轨迹，但是响应速度较慢；复合IMC控制的输出信号能够较好地跟踪目标轨迹，且具有较高的跟踪精度。

4 结论

通过对伺服阀控非对称缸系统的机理建模，结合参数辨识手段，获得了并联稳定平台液压驱动单元的具体数学模型。在此基础上，提出了基于速度前馈复合内模控制策略，通过仿真分析和实验验证，实现了舰船稳定平台液压驱动单元的高精度跟踪控制。相比于PID控制，该控制算法响应过渡平稳，抗干扰性和鲁棒性强；相比于内模控制，该控制算法响应快，精度高，且双向运动都能获得良好的动态性能。

基于速度前馈复合内模控制方法参数调节规则简单，便于工程实现。同时，基于速度前馈复合内模控制方法也存在对模型依赖程度较高的不足，设计一套完整的参数确定步骤，将有助于该方法在机构控制领域的进一步推广。

[1] 吴军，李铁民，关立文.飞行模拟器运动平台的计算力矩控制[J].清华大学学报:自然科学版，2006，46(8):1405-1408. WU Jun, LI Tiemin , GUAN Liwen. Computed-torque Control for a Moving Flight Simulator Platform[J]. Journal of Tsinghua University, 2006, 46(8):1405-1408.

[2] SHANG W, CONG S. Nonlinear Adaptive Task Space Control for a 2DOF Redundantly Actuated Parallel Manipulator[J]. Nonlinear Dynamics, 2010, 59(1):61-72.

[3] 何景峰，谢文建，韩俊伟.六自由度并联机器人输出解耦控制[J].哈尔滨工业大学学报,2006，38(3): 395-398. HE Jingfeng, XIE Wenjian, HAN Junwei. Output Decoupling Control of 6-DOF Parallel Manipulator[J]. Journal of Harbin Institute of Technology, 2006, 38(3):395-398.

[4] 刘长年. 非对称伺服油缸的动态研究[J]. 机床与液压，1985(1):1-10. LIU Changnian.Dynamic Study of Asymmetric Servo Cylinder[J].Machine Tool&Hydraulic,1985(1):1-10.

[5] 杨军宏. 三自由度船舶运动模拟平台及其液压伺服驱动系统的研究[D]. 长沙：国防科学技术大学，2007. YANG Junhong. Research on Ship Motion Simulator with Three Degrees of Freedom and Its Hydraulic Servo Driven System[D]. Changsha:NationalUniversity of Defense Technology,2007.

[6] 柏艳红，权龙，郝小星，等. 基于流量近似的阀控液压缸动力机构建模[J]. 机械工程学报，2014,50(24):179-185. BAI Yanhong, QUAN Long, HAO Xiaoxing, et al. Modeling of Hydraulic Valve-controlled Cylinder Power Mechanism Based on Flow Approximation[J]. Journal of Mechanical Engineering, 2014, 50(24):179-185.

[7] 王春行. 液压控制系统[M]. 北京: 机械工业出版社，1999: 113-115. WANG Chunxing.Hydraulic Control System[M].Beijing:China Machine Press，1999: 113-115.

[8] HARNEFORS L, NEE H P. Model-based Current Control of AC Machines Using the Internalmodel Control Method[J]. IEEE Transactions on Industry Applications,1998,34(1):133-141.

[9] GUARDABASSI G O, SAVARESI S M. Virtual Reference Direct Design Method: an Off-line Approach to Data-based Control System Design[J]. IEEE Transactions on Automatic Control, 2000, 45(5):954-959.

[10] 王正齐，刘贤兴. 基于神经网络逆系统的无轴承异步电机非线性内模控制[J]. 自动化学报， 2013，39(4): 433-439. WANG Zhengqi, LIU Xianxing. Nonlinear Internal Model Control for Bearingless Induction Motor Based on Neural Network Inversion[J]. Acta Automatica Sinica, 2013, 39(4):433-439.

[11] 杜杰.基于加速度计的光电伺服跟踪系统前馈控制[D].长春:中国科学院长春光学积木机械与物理研所,2011. DU Jie.Feed-forward Control for an Opto-electronics Servo Tracking System Based on Acelerometer[D].Changchun: Changchun Institute of Optics, Fine Mechanics and Physics Chinese Academy of Science,2011.

[12] 陈树宗，张殿华，孙杰，等. 液压弯辊控制系统的建模及辨识[J]. 东北大学学报:自然科学版，2012， 33(2):208-212. CHEN Shuzong, ZHANG Dianhua,SUN Jie, et al. Modeling and Identification of Hydraulic Bending Roll Control System[J]. Journal of Northeastern University, 2012, 33(2):208-212.

(编辑 王艳丽)

Study on Composite IMC of an Electro Hydraulic Drive Unit of Parallel Stable Platform

ZHANG Lijie1,2WANG Lihang1LI Shaohua1LI Yongquan2,3

1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University, Qinhuangdao, Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science, Yanshan University, Ministry of Education of China, Qinhuangdao,Hebei,066004 3.Hebei Provincial Key Laboratory of Parallel Robot and Mechatronic System,Yanshan University，Qinhuangdao,Hebei,066004

According to the requirements of motion control of a hydraulic driven ship stable platform, a composite IMC scheme was proposed based on velocity feed-forward structure. The mathematical model of the control object was obtained by the method of mechanism modeling and parameter identification, which was based on the single channel hydraulic drive unit of the ship stable platform. Simulation and experimental studies of the proposed control method were carried out，and the results show that, with the proposed control method, the tracking performance may be improved, as well as the anti-interference and robustness of the system.

shipstable platform; hydraulic drive unit; speed-forward structure; composite internal model control(IMC)

2016-04-05

国家自然科学基金资助项目(51405421，51275438)；河北省自然科学基金资助项目(E2015203101)

TH137

10.3969/j.issn.1004-132X.2017.05.014

张立杰，男，1969年生。燕山大学机械工程学院教授、博士研究生导师。主要研究方向为电液控制系统、机构学及机器人技术。发表论文50余篇。E-mail:ljzhang@ysu.edu.cn。王力航，男，1989年生。燕山大学机械工程学院博士研究生。李少华，男，1988年生。燕山大学机械工程学院硕士研究生。李永泉(通信作者)，男，1979年生。燕山大学机械工程学院副教授。