减振器阻尼对扭力梁疲劳寿命的影响
周 兵 李 宁 吴晓建 姜高松
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
减振器阻尼对扭力梁疲劳寿命的影响
周 兵 李 宁 吴晓建 姜高松
湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
为了研究减振器阻尼对扭力梁疲劳寿命的影响,建立了扭力梁有限元模型以及刚柔耦合整车模型。通过试验采集强化路面道路载荷谱作为整车模型的输入激励,仿真得到疲劳寿命分析所需文件,利用模态应力恢复法对扭力梁进行疲劳寿命分析,并通过扭力梁耐久性台架试验证明了仿真模型与疲劳寿命分析方法的准确性。仿真得到了不同阻尼系数下的扭力梁疲劳寿命分布云图以及最小疲劳寿命循环数,分析结果总结出了减振器阻尼大小对扭力梁本体疲劳寿命的影响规律。
扭力梁;减振器阻尼;模态应力恢复;疲劳寿命
0 引言
扭力梁式后悬架质量轻,成本低,紧凑性好,被广泛应用于小型乘用车上。扭力梁悬架承担了后轴大部分的载荷,因此对其耐久性有较高的要求,提高扭力梁的疲劳寿命成为扭力梁悬架系统设计的重要目标。国内外一些科研人员应用不同的方法对扭力梁耐久性作了研究,罗明军等[1]结合多体动力学仿真技术以及有限元分析方法,通过获得的后扭力梁轴头的载荷信息,较为准确地预测了扭力梁的疲劳寿命;蒋荣超等[2]利用名义应力法对扭力梁本体进行疲劳寿命分析并在此基础上进行了轿车轻量化设计;艾传智等[3]用多种方法对扭力梁疲劳寿命进行仿真并对比分析了各方法的优劣;LYU等[4]针对扭力梁的弹性运动建立了较为精确的模型,并利用此模型对扭力梁截面参数进行了优化。然而这些研究都是从扭力梁本身结构出发,更多的是研究扭力梁本体结构对疲劳寿命的影响。扭力梁悬架是一个包括弹簧、减振器的系统,扭力梁的疲劳寿命不仅与其本身结构有关,与减振器阻尼也有非常密切的关系。
基于此,本文分析了减振器阻尼对扭力梁疲劳寿命的影响。首先利用有限元软件和多体动力学仿真软件,建立扭力梁有限元模型以及刚柔耦合整车模型,加载试验场采集的道路载荷谱,得到疲劳寿命分析所需的时间-位移历程文件,然后采用模态应力恢复法分析得到原减振器阻尼下的扭力梁疲劳寿命,并通过扭力梁台架试验验证了分析方法的正确性与建立模型的准确性。在此基础上分析得到了不同减振器阻尼下扭力梁疲劳寿命云图与最小疲劳寿命循环数,分析总结了减振器阻尼对扭力梁疲劳寿命的影响规律。
1 疲劳寿命分析理论与减振器阻尼可行设计区间
1.1 模态分析
模态分析是模态应力恢复法分析疲劳寿命的前提和基础。在自由模态(无外载荷、无阻尼)的情况下,模型所对应的运动方程[5]为
Kθsinωt-ω2Mθsinωt=0
(1)
将式(1)进行简化,得到下式:
(K-ω2M)θ=0
(2)
式中,K为刚度矩阵;ω为圆频率;M为质量矩阵;θ为特征向量(振型)[6]。
式(2)有一组解的条件为
det(K-ωM)=0
(3)
由式(3)可得第i阶固有频率ωi和相对应的特征向量(振型)θi。在自由(或强迫)振动下线弹性结构在任意时刻的振动形状是所有模态的线性组合,即
u=∑θiξi
(4)
式中,u为某单个节点的节点位移;ξi为第i阶模态位移。
1.2 基于模态分析的柔体动力学
在建立动力学模型时,需要采用模态中性文件(柔性体文件)来代替原刚性文件以提高系统的仿真精度。具体实现的方式是:首先利用离散化的有限元文件生成柔性体文件,然后赋予柔性体文件一个模态集,根据模态展开法采用模态坐标和模态向量的线性组合来表示弹性位移,而柔性体的变形则以计算得到的每一时刻的弹性位移来进行描述。
设τ为柔性体上任意某点在总体坐标系中的坐标,即
τ=(x,y,z,ψ,α,φ,ξi)T=(R,Γ,Φ)T
(5)式中,x、y、z为局部坐标系在总体坐标中的位置;ψ、α、φ为局部坐标系在总体坐标系中的欧拉角;R、Γ为两坐标系中坐标的矢量表达;Φ为ξi的矢量表达,即模态位移矢量。
根据拉格朗日方程[7],柔性体的动力学方程表示为
(6)
式(6)可以简化为
(7)
式中,C为阻尼矩阵;λ为与约束方程Ω相对应的拉氏乘子;G为重力;Q为广义力;F0为外力矩阵。
1.3 模态应力恢复与疲劳寿命分析
依据模态应力恢复法,可以求得作用在有限元模型上的反作用力F和模态应力σ:
F=KU-ω2MU
(8)
σ=θEσ
(9)
式中,U为基于模态位移矢量和模态振型矢量的节点位移;Eσ为模态应力矩阵。
在正常行驶条件下,汽车扭力梁的疲劳失效为高周疲劳破坏,按照Miner损伤积累法则,疲劳寿命公式为
S=1/D
(10)
式中,S为疲劳寿命;D为总疲劳损伤[8]。
1.4 悬架系统阻尼可行设计区间
悬架系统减振器应首先考虑悬架的安全性与舒适性。基于舒适性的车辆悬架最佳阻尼比[9]
(11)
式中,rm为质量比;ms为簧上质量;mu为簧下质量;rk为刚度比;kt为轮胎刚度;k为弹簧刚度。
基于安全性的车辆悬架最佳阻尼比[9]
(12)
根据式(11)和式(12)可以得到被动悬架减振器的阻尼可行设计区间。
1.5 基于模态应力恢复的扭力梁疲劳寿命分析技术路线
采用模态应力恢复法分析扭力梁疲劳寿命的技术路线如图1所示。
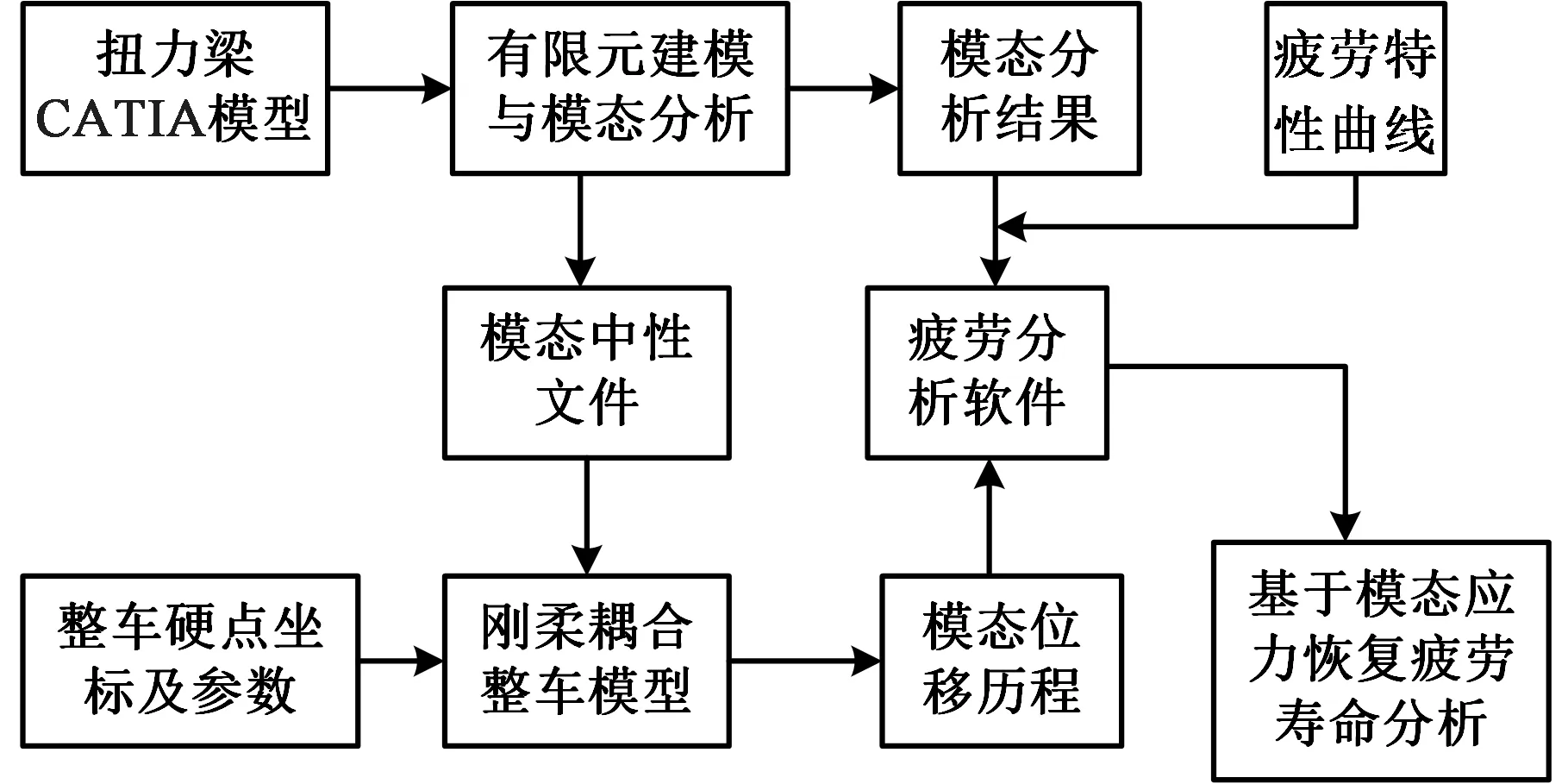
图1 扭力梁疲劳寿命分析技术路线Fig.1 Technical route of fatigue life analysis
2 模态分析与刚柔耦合模型建立
建立扭力梁有限元模型,应用壳单元进行焊缝的模拟,利用壳单元模拟焊缝可以更好地模拟实际载荷的传递机理[10],然后,在有限元软件MSC.Patran中进行模态分析。
图2为扭力梁第7阶模态分析云图。第7阶模态为扭力梁整体扭转模态,是造成扭力梁疲劳损伤的主要模态之一。模态分析中,前6阶自由模态为扭转梁的刚性模态,不予考虑,另外,高阶振型对扭力梁结构的动力特性影响也非常小,所以也不予考虑。本文取扭力梁模态分析的前16阶非零自由模态特征参数,具体如表1所示。

图2 第7阶模态分析结果Fig.2 Modal analysis of mode 7

表1 扭力梁7~16阶非零模态分析结果
柔性体文件包含了模态分析的所有信息,扭力梁的柔性体文件可以借助软件Hyperworks生成,在ADAMS/Car中根据试验样车硬点坐标进行整车建模,并用扭力梁柔性体替换掉原刚性体,建好的刚柔耦合整车模型如图3所示。

图3 刚柔耦合整车模型Fig.3 Rigid-flexible coupling vehicle modal
3 模态应力恢复法疲劳寿命分析
3.1 道路载荷谱的收集与时间历程的获取
车轮六分力传感器可以实时测量车辆实际行驶工况中地面作用于轴头的六分力,近年来被广泛应用于道路载荷谱采集试验中,为虚拟车辆模型提供路面驱动及标称载荷信号。本文利用车轮六分力传感器在试验场强化路面上采集道路载荷谱,并通过虚拟迭代方式将轮心垂向力等效为垂向载荷(垂向载荷对扭力梁疲劳寿命影响最为显著[11])。
在ADAMS/Car中进行四立柱试验台的仿真试验,对刚柔耦合整车模型的车轮(轮心)施加激励,模拟车辆在真实路面的行驶状况。实现整车模型仿真试验可以用实时采样的数据模拟汽车行驶在粗糙路面的响应特性。将在试验场采集的强化路面的载荷谱等效垂向位移作为四立柱试验台的输入。采集的道路谱时长为700 s,对应一个循环为9.22 km。在ADAMS/Car中仿真时长设置为700 s,扭力梁柔性体文件可以将各阶模态位移的时间历程记录下来。图4为扭力梁柔性体记录的第7阶模态时间位移历程。

图4 第7阶模态时间-位移历程Fig.4 Modal displacement time history of mode 7
3.2 模态应力恢复法疲劳寿命预测与试验验证
把获得的模态位移历程作为载荷时间历程,与各阶模态的模态应力相结合,然后根据材料的疲劳特性曲线(S-N曲线)设置求解方法,在疲劳分析软件MSC.fatigue中对扭力梁进行虚拟疲劳试验分析[12],并采用Goodman图对平均应力影响进行修正,即可得到虚拟疲劳试验分析结果。
在如图5所示的扭力梁耐久性台架试验台上进行扭力梁的垂向耐久性试验。具体试验方法为:按照试验样车参数将扭力梁、减振器及弹簧等安装到试验台上,两个作动缸分别向控制连杆安装点位置施加沿垂直向的变幅位移信号。两个作用缸的位移信号同样为试验场采集的强化路面的载荷谱等效垂向位移,进行高周疲劳试验,测得扭力梁疲劳寿命较为薄弱区域,并与虚拟疲劳分析试验进行对比。由试验结果与虚拟疲劳分析结果对比可知:经高周疲劳试验,扭力梁在试验中的寿命较薄弱区域(图6中S1、S2、S3区域)为横梁部分区域以及横梁和曳臂焊接的区域,与图中运用模态综合法计算得到的疲劳寿命薄弱区域(图6中P1、P2、P3区域)吻合,证明了利用模态应力恢复法进行的疲劳寿命仿真分析能够准确地反映扭力梁本体疲劳损伤的情况,同时也验证了刚柔耦合整车模型以及虚拟疲劳试验分析的准确性。

图5 扭力梁耐久性台架试验安装图Fig.5 Durability test bench of twist beam

图6 试验与仿真对比图Fig .6 Comparision between simulation and testing mode
4 减振器对疲劳寿命的影响
4.1 减振器阻尼特性试验
关于减振器的研究中有以下3个重要的特性曲线: 阻尼力-位移曲线、准静态以及动态阻尼力-速度特性曲线[13]。本文采用准静态阻尼力-速度特性曲线来描述减振器阻尼特性。使减振器在恒定的激振频率下运动,激振振幅改变,通过各阻尼力-位移曲线中的最大阻尼力以及相应的最大速度得到减振器特性试验数据,如表2所示。其中,l为减振器活塞行程,v为激振速率,FDmax为最大阻尼力,FDmin为最小阻尼力。

表2 减振器试验数据Tab.2 Thetest data of shock absorber
4.2 阻尼系数与减振器阻尼可行设计区求解
减振器阻尼系数cD和衰减指数n与频率无关,它们与减振器阻尼力FD以及减振器运动速度vD的关系为
(13)
阻尼系数和衰减指数描写了准静态阻尼力-速度特性曲线的走向,能够反映减振器的阻尼特性,其中阻尼系数影响曲线的斜度,而衰减指数影响曲线的凹凸趋势。将减振器特性曲线经过如图7所示的直线进行拟合后,减振器阻尼系数cD可用拟合直线的斜率来表示。
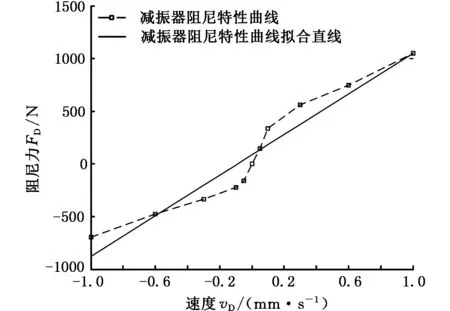
图7 减振器阻尼特性曲线与拟合直线Fig.7 Damping characteristic curve and fitting line of shock absorber
经直线拟合后,试验样车所用减振器的阻尼系数为964.5N·s/m。阻尼系数与基于舒适性的车辆悬架最佳阻尼比ζoc、基于安全性的车辆悬架最佳阻尼比ζos的关系如下:
(14)
(15)
已知试验样车扭力梁后悬架弹簧刚度和轮胎刚度,由式(14)、式(15)确定的满载工况下的阻尼比范围为0.1828~0.3494,减振器阻尼系数范围为926~1770N·s/m。
4.3 不同阻尼时扭力梁疲劳寿命分析求解
改变减振器阻尼特性曲线拟合直线的斜率可以达到改变减振器的阻尼系数的目的。在原始减振器的线性拟合阻尼cD的基础上,分别取1.1cD,1.2cD,1.3cD,1.4cD,1.5cD,1.6cD,1.7cD,1.8cD(所取阻尼均在可行设计区926~1770N·s/m以内)。通过虚拟疲劳分析试验分别得到各减振器阻尼系数下的扭力梁的疲劳寿命分析云图(图8)。
从图8、图9可以看出,在试验样车减振器阻尼可行设计区域内,随着减振器阻尼系数大小的改变,扭力梁的疲劳寿命分析结果会发生相应的改变。随着减振器阻尼系数的变大,疲劳寿命较为薄弱的区域的面积有逐渐变小的趋势,如图9所示,阻尼为1.8cD时的疲劳寿命薄弱区域面积分别为SA2、SB2、SC2、SD2,明显小于阻尼为1.0cD时疲劳寿命薄弱区域面积SA1、SB1、SC1、SD1。

图8 不同减振器阻尼系数的疲劳寿命分析云图Fig.8 Fatigue life contours of twist beam with different damper damping coefficient
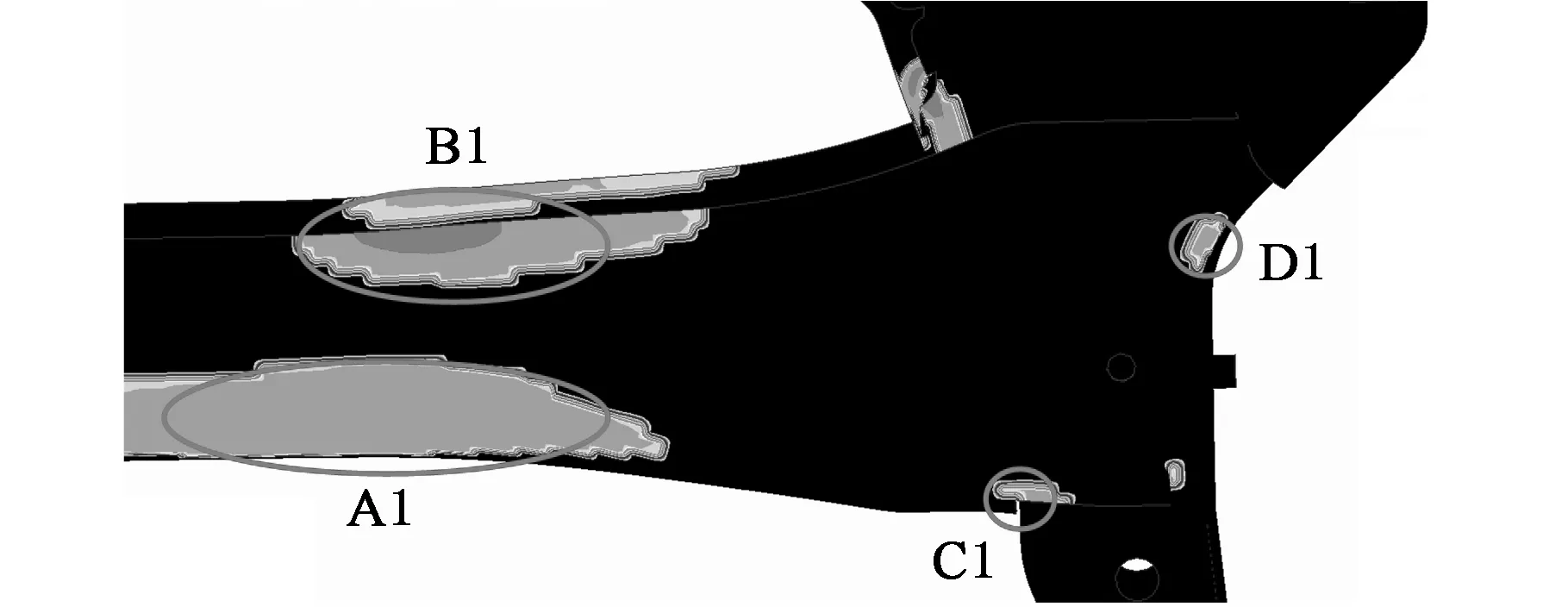
(a)阻尼为1.0cD

(b)阻尼为1.8cD图9 1.0cD与1.8cD阻尼下疲劳寿命分析比较图Fig.9 Comparision between 1.0cD and 1.8cD
将扭力梁最小疲劳寿命(循环次数)变化用直线拟合,结果如图10所示。

图10 最小疲劳寿命(循环次数)变化趋势拟合结果Fig.10 Fitting line of minimum fatigue life
由图10可以发现:在虚拟疲劳分析试验中,为了简化问题,可以将减振器阻尼特性曲线用直线进行拟合,并求得拟合直线相对应的阻尼系数;改变阻尼系数的大小,利用疲劳分析软件可以分析得到不同阻尼下疲劳寿命云图以及最小疲劳寿命循环次数;最小疲劳寿命(循环次数)随着减振器阻尼系数的增大而增大。
5 结论
(1)通过建立扭力梁有限元模型以及刚柔耦合整车模型,基于试验采集真实道路载荷谱,利用模态综合法对扭力梁进行疲劳寿命仿真分析,并且通过试验验证了模型建立的准确性以及疲劳计算方法的正确性。
(2)通过分析不同减振器阻尼系数下疲劳寿命云图,得出减振器阻尼对扭力梁本体的疲劳寿命有很大影响的结论。即在减振器阻尼的可行设计区域内,随着减振器阻尼系数的增大,疲劳薄弱区域的面积有显著减小,同时扭力梁本体最小疲劳寿命也随之增加。因此在提高扭力梁疲劳寿命时,不仅可以从扭力梁本体进行结构(如厚度、形貌等)的改进,还可以通过减振器的设计来提高扭力梁的疲劳寿命。
(3)另外,减振器阻尼会影响扭力梁的疲劳寿命,因此在进行减振器的设计时,除了要进行传统的平顺性和操纵稳定性的匹配,还应该考虑减振器对扭力梁的寿命影响。
[1] 罗明军, 侯之超, 宋立新,等. 后扭力梁轴头载荷谱仿真及疲劳寿命预测[J]. 西安交通大学学报, 2013, 47(9):106-111. LUO Mingjun,HOU Zhichao,SONG Lixin,et al. Simulation of Load Time History of Spindle Nose and Fatigue Life Prediction for Rear Torsion Beam[J]. Journal of Xi’an Jiaotong University,2013,47(9):106-111.
[2] 蒋荣超, 王登峰, 秦民,等. 基于疲劳寿命的轿车后悬架扭转梁轻量化设计[J]. 吉林大学学报:工学版, 2016,46(1):35-42. JIANG Rongchao,WANG Dengfeng,QIN Min ,et al.Light Weight Design of Twist Beam of Rear Suspension of Passenger Car Based on Fatigue Life[J]. Journal of Jilin University (Engineering and Technology Edition),2016,46(1):35-42.
[3] 艾传智, 陈建华, 肖攀,等. 基于真实道路载荷谱后扭力梁疲劳寿命分析[C]//2009中国汽车工程学会年会. 北京,2009:1-7. AI Chuanzhi,CHEN Jianhua,XIAO Pan ,et al.Fatigue Life Analysis of Twist Beam Based on Real Road Load[C]// 2009 China Soeiety of Automotive Engineers Annual Meeting.Beijing,2009:1-7.
[4] LYU N, PARK J, URABE H, et al. Design of Automotive Torsion Beam Suspension Using Lumped-Compliance Linkage Models[C]// ASME 2006 International Mechanical Engineering Congress and Exposition. NewYork: American Society of Mechanical Engineers, 2006:219-228.
[5] 姚卫星. 结构疲劳寿命分析[M].北京:国防工业出版社, 2003:88-100. YAO Weixing. Fatigue Life Prediction of Structures [M].Beijing:National Defense industry Press,2003:88-100.
[6] 曹树谦, 张文德, 萧龙翔. 振动结构模态分析:理论、实验与应用[M]. 天津:天津大学出版社, 2001:18-22. CAO Shuqian,ZHANG Wende,XIAO Longxiang. Modal Analysis of Vibration Structures: Theory.Experiment and Application[M]. Tianjin: Tianjin University Press,2001:18-22.
[7] KYUBA H, DONG P. Equilibrium-equivalent Structural Stress Approach to Fatigue Analysis of a Rectangular Hollow Section Joint[J]. International Journal of Fatigue, 2005, 27(1):85-94.
[8] 王国军. MSC.FATIGUE疲劳分析实例指导教程 [M]. 北京:机械工业出版社, 2009:38-51 WANG Guojun. MSC.FATIGUE Examples and Tutorials of Fatigue Analysis[M]. Beijing: China Machine Press,2009:38-51.
[9] 周长城. 汽车平顺性与悬架系统设计[M]. 北京:北京机械工业出版社, 2011:79-89 ZHOU Changcheng. Vehicle Ride Comfort and Suspension System Design[M]. Beijing: China Machine Press,2011:79-89.
[10] 黄圳圭,赵志健.大型航天器动力学与控制[M].长沙:国防科技大学出版社,1990:203-215. HUANG Zhengui, ZHAO Zhijian. Dynamics and Control of Large Spacecraft[M]. Changsha: National University of Defense Technology Press,1990:203-215.
[11] ZHAO L H, ZHENG S L, FENG J Z. Failure Mode Analysis of Torsion Beam Rear Suspension under Service Conditions[J]. Engineering Failure Analysis, 2014, 36(1):39-48.
[12] 万茂林. 扭力梁式后悬架总成疲劳损伤研究[D]. 武汉:武汉理工大学, 2013. WAN Maolin.Research on Fatigue Damage of Torsion Beam Suspension[D]. Wuhan:Wuhan University of Technology,2013.
[13] 艾小娇, 章桐. 汽车减震器特征参数的建立与评价[J]. 上海汽车, 2014(4):38-41. AI Xiaojiao,ZHANG Tong. Establishment and Evaluation of Characteristic Parameters of Automobile Shock Absorber[J]. Shanghai Auto, 2014(4):38-41.
(编辑 王艳丽)
Effects of Shock Absorber Damping on Fatigue Lifes of Torsion Beams
ZHOU Bing LI Ning WU Xiaojian JIANG Gaosong
State Key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha, 410082
In order to study the effects of shock absorber damping on the fatigue lifes of the torsion beams, the finite element model and rigid flexible coupling model were set up. The road load spectrum collected by experiments on strengthened test pavement was used as the input excitation of the vehicle model, and documents of the fatigue analysis could be gotten by the simulation , then the fatigue analyses of torsion beams could be conducted by modal stress recovery, the accuracy of the results could be proved by the bench text of durability. Finally, the contours of fatigue lifes and the minimum fatigue life cycle with different damping coefficients would be obtained ,and the effects of the shock absorber damping on fatigue lifes of the torsion beams might be known.
torsion beam;shock absorber damping;modal stress recovery;fatigue life
2016-04-15
国家自然科学基金资助项目(51275162,51575167);国家重点研发计划资助项目(2016YFB0100903-2);智能型新能源国家2011协同创新中心、湖南省绿色汽车协同创新中心资助项目
U463.1
10.3969/j.issn.1004-132X.2017.05.007
周 兵,男,1972年生。湖南大学机械与运载工程学院副教授、博士后研究人员。主要研究方向为车辆动力学及其控制、车辆结构分析与优化。获中国专利4项。发表论文50余篇。E-mail:zhou_bingo@163.com。李 宁(通信作者),男,1991年生。湖南大学机械与运载工程学院硕士研究生。吴晓建,男,1985年生。湖南大学机械与运载工程学院博士研究生。姜高松,男,1989年生。湖南大学机械与运载工程学院硕士研究生。

